Проверка двудольности: практическое применение поиска в ширину - Графы

Вспомним определение двудольного графа: так называется граф, множество узлов V которого может быть разбито на такие подмножестваX и Y, что один конец каждого ребра принадлежит X, а другой конец принадлежит Y. Чтобы обсуждение было более наглядным, представьте, что узлы множества X окрашены в красный цвет, а узлы множества Y — в синий. Тогда можно сказать, что граф является двудольным, если его узлы можно раскрасить в красный и синий цвет так, чтобы у каждого ребра один конец был красным, а другой синим.

Задача

В предыдущих главах приводились примеры двудольных графов. Для начала зададимся вопросом: существуют ли естественные примеры недвудольных графов, то есть графов, для которых такое разбиение V невозможно?

Разумеется, треугольник не может быть двудольным: первый узел окрашивается в красный цвет, другой в синий, а с третьим уже ничего не сделать. В более общем смысле возьмем цикл Cнечетной длины с пронумерованными узлами 1, 2, 3, ..., 2k, 2k + 1. Если раскрасить узел 1 в красный цвет, то узел 2 должен быть окрашен в синий цвет, после чего узел 3 окрашивается в красный и т. д.; нечетные узлы окрашиваются в красный цвет, а четные в синий. Но тогда узел 2k + 1 должен быть красным, и от него ведет ребро к узлу 1 — тоже красному. Следовательно, разбить C на красные и синие узлы так, как требуется по условию задачи, невозможно. Обобщая далее, мы видим, что если граф G просто содержит нечетный цикл, можно применить тот же аргумент; следовательно, мы приходим к следующему утверждению.

(3.14) Если граф G является двудольным, он не может содержать нечетные циклы.

Легко проверить, что граф является двудольным, если соответствующие множества X и Y (то есть красные и синие узлы) уже были определены за нас; и во многих ситуациях, в которых встречаются двудольные графы, это естественно. Но предположим, имеется граф G без информации о разбиении, и нам хотелось бы определить, является ли граф двусторонним, то есть существует ли требуемое разбиение на красные и синие узлы. Насколько сложна эта задача? Из (3.14) видно, что одним из простых препятствий к двудольности графа является наличие нечетных циклов. Существуют ли другие, более сложные препятствия?

Проектирование алгоритма

На самом деле существует очень простая процедура проверки двудольности, а из ее анализа следует, что других препятствий, кроме нечетных циклов, нет. Сначала предположим, что граф Gявляется связным, поскольку в противном случае мы могли бы сначала вычислить его компоненты связности и проанализировать каждую из них по отдельности. Затем мы выбираем любой узел s ∈ V и окрашиваем его в красный цвет; никакой потери общности при этом не происходит, так как s все равно должен быть связан с каким-то цветом. Все соседи 5 должны быть окрашены в синий цвет, мы так и поступаем. Все соседи этих узлов окрашиваются в красный цвет, их соседи в синий и т. д., пока не будет раскрашен весь граф. В этот момент у нас либо появляется действительная красно-синяя окраска G, в которой каждое ребро имеет разноцветные концы, либо у какого-то ребра концы имеют одинаковый цвет. Похоже, в последнем случае ничего сделать было нельзя: просто граф G не является двудольным. Теперь это обстоятельство нужно обосновать более формально, а также выработать эффективный способ раскраски.

Прежде всего следует заметить, что описанная процедура окрашивания по сути идентична описанию BFS: мы перемещаемся вперед от 5, раскрашивая узлы, когда они впервые попадаются в процессе перебора. Более того, алгоритм окрашивания можно описать следующим образом: мы выполняем поиск BFS, узел 5 окрашивается в красный цвет, все узлы уровня L₁ — в синий, все узлы уровня L₂ в красный и так далее. Нечетные уровни окрашиваются в синий цвет, а четные — в красный.

Чтобы реализовать это описание на базе BFS, достаточно взять реализацию BFS и добавить дополнительный массив Color. При каждом шаге BFS, на котором узел v добавляется в список L[i + 1], выполняется присваивание Color[v] = red, если i + 1 является четным числом, или Color[v] = blue, если i + 1 нечетное. В конце этой процедуры остается перебрать все ребра и определить, не был ли присвоен обоим концам одинаковый цвет. Следовательно, общее время выполнения алгоритма окрашивания составляет O(m + n), как и для алгоритма BFS.

Анализ алгоритма

Теперь можно доказать утверждение о том, что этот алгоритм правильно определяет, является ли граф двудольным. Также оно показывает, что если граф G не является двудольным, в нем можно найти нечетный цикл.

(3.15) Пусть G — связный граф, а L₁, L₂, ... — уровни, построенные алгоритмом BFS, начиная с узла s. В этом случае должно выполняться ровно одно из следующих двух условий.

(i) В G не существует ребра, соединяющего два узла одного уровня. В таком случае G является двудольным графом, в котором узлы четных уровней могут быть окрашены в красный цвет, а узлы нечетных уровней — в синий цвет.

(ii) В G существует ребро, соединяющее два узла одного уровня. В этом случае G содержит цикл нечетной длины, а следовательно, не может быть двудольным.

Доказательство. Сначала рассмотрим случай (i): предположим, не существует ребра, соединяющего два узла одного уровня. В соответствии с (3.4) мы знаем, что каждое ребро G соединяет узлы либо одного уровня, либо смежных уровней. Предположение для случая (i) заключается в том, что первая из двух вариантов альтернатив не встречается, то есть каждое ребро соединяет два узла смежных уровней. Но наша процедура окрашивания назначает смежным уровням противоположные цвета, поэтому каждое ребро имеет разноцветные концы. Следовательно, описанная схема окрашивания обеспечивает двудольность G.

Теперь допустим, что выполняется условие (ii); почему граф G обязан содержать нечетный цикл? Известно, что G содержит ребро, соединяющее два узла одного уровня. Допустим, это ребро e= (х, у), при этом х, y ∈ L_j. Кроме того, для удобства записи будем считать, что L₀ (“уровень 0”) представляет собой множество, состоящее только из s. Теперь возьмем дерево BFS T, построенное нашим алгоритмом, и обозначим z узел наивысшего возможного уровня, для которого z является предком как х, так и у в дереве T; по очевидным причинам z можно назвать низшим общим предком х и у. Допустим, z ∈ L_i, где i < j. Возникает ситуация, изображенная на рис. 3.6. Рассмотрим цикл C, определяемый переходом по пути z-x в T, затем по ребру e и затем по пути y-z в T. Длина этого цикла, вычисляемая суммированием длин трех частей, равна (j - i) + 1 + (j - i); получается 2( j - i) + 1, то есть нечетное число. ■

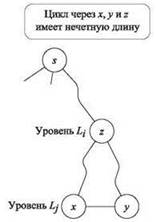
Рис. 3.6. Если два одноуровневых узла х и у соединены ребром, то цикл через х, у и их низшего общего предка z имеет нечетную длину; это показывает, что граф не может быть двудольным