Первая задача: устойчивые паросочетания - Введение: некоторые типичные задачи

Начнем с рассмотрения алгоритмической задачи, неплохо демонстрирующей многие темы, которым будет уделяться особое внимание в этой книге. Эта задача обусловлена вполне естественными и практическими соображениями, на основе которых будет сформулирована простая и элегантная постановка задачи. Алгоритм решения задачи также очень элегантен, поэтому большая часть нашей работы будет потрачена на доказательство того, что алгоритм работает правильно, а время, необходимое для его завершения и получения ответа, лежит в допустимых пределах. Происхождение самой задачи, известной как задача о поиске устойчивых паросочетаний (далее “задача устойчивых паросочетаний”), имеет несколько источников.

Задача

Задача устойчивых паросочетаний была частично сформулирована в 1962 году, когда два экономиста-математика, Дэвид Гейл и Ллойд Шепли, задались вопросом: можно ли спланировать процесс поступления в колледж (или приема на работу), который был бы саморегулируемым (self-enforcing)? Что они имели в виду?

Давайте сначала неформально рассмотрим, какие ситуации могут возникнуть, если группа студентов колледжа начинает подавать заявки в компании на летнюю практику. Ключевым фактором в процессе обработки заявок становится взаимодействие двух разных сторон: компаний (нанимателей) и студентов (кандидатов). Каждый кандидат упорядочивает список компаний в порядке своих предпочтений, а каждая компания — после поступления заявок — формирует свой порядок предпочтений для кандидатов, подавших заявки. На основании этих предпочтений компании обращаются с предложениями к некоторым из своих кандидатов. Кандидаты решают, какое из полученных предложений стоит принять, и студенты отправляются на свою летнюю практику.

Гейл и Шепли рассмотрели всевозможные сбои, которые могут произойти в этом процессе при отсутствии каких-либо механизмов, обеспечивающих должный ход событий. Допустим, к примеру, что ваш друг Радж только что принял предложение от крупной телекоммуникационной компании CluNet. Через несколько дней начинающая компания WebExodus, которая тянула с принятием нескольких окончательных решений, связывается с Раджем и тоже предлагает ему летнюю практику. Вообще-то, с точки зрения Раджа, вариант с WebExodus предпочтительнее CluNet — скажем, из-за непринужденной атмосферы и творческого азарта. Этот поворот заставляет Раджа отказаться от предложения CluNet и пойти в WebExodus. Лишившись практиканта, CluNetпредлагает работу одному из запасных кандидатов, который мгновенно отменяет свое предыдущее согласие на предложение мегакорпорации Babelsoft. Ситуация набирает обороты и постепенно выходит из-под контроля.

С другого направления все выглядит ничуть не лучше, а то и хуже. Допустим, подруге Раджа по имени Челси было назначено отправиться в Babelsoft. Но услышав историю Раджа, она звонит в WebExodus и говорит: “Знаете, я бы предпочла провести это лето в вашей фирме, а не в Babelsoft”. Отдел кадров WebExodus охотно верит; более того, заглянув в заявку Челси, они понимают, что она перспективнее другого студента, у которого уже запланирована летняя практика. И если компания WebExodus не отличается особой деловой принципиальностью, она найдет способ отозвать свое предложение другому студенту и возьмет Челси на его место.

Такие ситуации быстро порождают хаос, и многие участники — как кандидаты, так и наниматели — могут оказаться недовольны как самим процессом, так и его результатом. Что же пошло не так? Одна из основных проблем заключается в том, что процесс не является саморегулируемым; если участникам разрешено произвольно действовать, исходя из их собственных интересов, весь процесс может быть нарушен.

Пожалуй, вы бы предпочли следующую, более устойчивую ситуацию, в которой сами личные интересы участников предотвращают отмену и перенаправление предложений. Допустим, другой студент, который должен был провести лето в CluNet, звонит в WebExodus и сообщает, что он бы предпочел поработать на них. Но на основании уже принятых предложений ему отвечают: “Нет, каждый из принятых нами кандидатов предпочтительнее вас, поэтому мы ничего не сможем сделать”. Или возьмем нанимателя, который преследует лучших кандидатов, распределенных по другим фирмам, но получает от каждого из них ответ: “Спасибо, но мне и здесь хорошо”. В таком случае все результаты устойчивы — никакие дальнейшие “перетасовки” невозможны.

Итак, вот как выглядел вопрос, заданный Гейлом и Шепли: можно ли для имеющегося набора предпочтений по кандидатам и нанимателям распределить кандидатов по нанимателям так, чтобы для каждого нанимателя E и каждого кандидата A, который не был принят на работу к E, выполнялось по крайней мере одно из следующих двух условий?

1. Каждый из кандидатов, принятых E на работу, с его точки зрения, предпочтительнее A; или

2. С точки зрения A, его текущая ситуация предпочтительнее работы на нанимателя E.

Если этот критерий выполняется, то результат устойчив (стабилен): личные интересы сторон предотвратят закулисные дополнительные договоренности между кандидатами и нанимателями.

Гейл и Шепли разработали блестящее алгоритмическое решение для задачи, которым мы сейчас займемся. Но сначала стоит заметить, что это не единственный источник происхождения задачи устойчивых паросочетаний. Оказывается, еще за десять лет до работы Гейла и Шепли очень похожая процедура, основанная на тех же соображениях, использовалась Национальной программой распределения студентов-медиков по больницам. Более того, эта система с относительно незначительными изменениями продолжает применяться и в наши дни.

Формулировка задачи

Чтобы добраться до сути концепции, задачу следует по возможности очистить от всего лишнего. В мире компаний и кандидатов существует асимметрия, которая только отвлекает от главного. Каждый кандидат подбирает одну компанию, но каждая компания подбирает нескольких кандидатов; более того, количество кандидатов может оказаться больше (или, как это бывает, меньше) количества доступных вакансий. Наконец, в реальной жизни каждый кандидат редко подает заявки во все имеющиеся компании.

По крайней мере на начальной стадии будет полезно устранить эти сложности и перейти к “упрощенной” постановке задачи: каждый из n кандидатов подает заявки в каждую из n компаний, а каждая компания хочет принять на работу одного кандидата. Вскоре вы увидите, что при этом сохраняются фундаментальные аспекты задачи; в частности, наше решение упрощенной версии можно будет напрямую расширить для более общего случая.

Вслед за Гейлом и Шепли мы заметим, что этот частный случай можно рассматривать как задачу разработки системы, в которой n мужчин и n женщин могут подыскать себе пару. В нашей задаче существует естественная аналогия для двух “полов” (кандидаты и компании), а в рассматриваемом случае каждый участник подыскивает себе ровно одного участника противоположного пола¹.

Итак, имеется множество M = {m₁, ..., m_n} из n мужчин и множество W = {w₁, ..., w_n} из n женщин. Пусть запись M х W обозначает множество всех возможных упорядоченных пар в форме (m, w), где m ∈ M и w ∈ W. Паросочетание² S представляет собой множество упорядоченных пар, каждая из которых входит в M х W, обладающее тем свойством, что каждый элемент M и каждый элемент W встречается не более чем в одной паре в S. Идеальным паросочетанием S' называется паросочетание, при котором каждый элемент M и каждый элемент W встречается ровно в одной паре из S'.

Мы еще не раз в книге вернемся к концепциям паросочетаний и идеальных паросочетаний; они естественным образом возникают при моделировании широкого диапазона алгоритмических задач. На текущий момент термин “идеальное паросочетание” соответствует способу формирования пар из мужчин и женщин таким способом, чтобы каждый оказался с кем-то в паре и никто не был включен более чем в одну пару — ни одиночество, ни полигамия.

Теперь в эту схему можно добавить понятие предпочтений. Каждый мужчина m ∈ M формирует оценки всех женщин; мы говорим, что m предпочитает w женщине w', если m присваивает wболее высокую оценку, чем w'. Мы будем называть упорядоченную систему оценок m его списком предпочтений. “Ничьи” в оценках запрещены. Аналогичным образом каждая женщина назначает оценки всем мужчинам.

Какие могут возникнуть проблемы с имеющимся идеальным паросочетанием S? В контексте исходной задачи с нанимателями и кандидатами возможна следующая неприятная ситуация: в Sприсутствуют две пары (m, w) и (m', w') (рис. 1.1), обладающие таким свойством, что m предпочитает w' женщине w, а w' предпочитает m мужчине m'. В таком случае ничто не помешает m и w' бросить своих партнеров и создать новую пару; такой набор пар не является саморегулируемым. В нашей терминологии такая пара (m, w') является неустойчивой по отношению к S: пара (m, w') не принадлежит S, но каждый из участников m и w' предпочитает другого своему текущему партнеру в S.

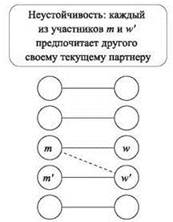
Рис. 1.1. Идеальное паросочетание S с неустойчивостью (m, w')

Итак, нашей целью является создание паросочетания без неустойчивых пар. Паросочетание S называется устойчивым, если оно (1) идеально и (2) не содержит неустойчивости в отношении S. Немедленно возникают два вопроса:

♦ Существует ли устойчивое паросочетание для каждого набора списков предпочтений?

♦ Можно ли эффективно построить устойчивое паросочетание для имеющегося списка предпочтений (если оно существует)?

Примеры

Для демонстрации этих определений будут рассмотрены два очень простых примера задачи устойчивых паросочетаний.

Для начала допустим, что имеется множество из двух мужчин {m, m'} и множество из двух женщин {w, w'}. Списки предпочтений выглядят так:

♦ m предпочитает w женщине w';

♦ m' предпочитает w женщине w';

♦ w предпочитает m мужчине m';

♦ w' предпочитает m мужчине m'.

Если рассматривать этот набор списков предпочтений на интуитивном уровне, он представляет ситуацию полного согласия: мужчины сходятся во мнениях относительно порядка женщин, а женщины — относительно порядка мужчин. В такой ситуации существует уникальное устойчивое паросочетание, состоящее из пар (m, w) и (m', w'). Другое идеальное паросочетание, состоящее из пар (m', w) и (m, w'), не является устойчивым, потому что пара (m, w) образует неустойчивость по отношению к этому паросочетанию. (Как m, так и w предпочли бы бросить своих партнеров и образовать новую пару.)

В следующем примере ситуация немного усложняется. Предположим, действуют следующие предпочтения:

♦ m предпочитает w женщине w';

♦ m' предпочитает w' женщине w;

♦ w предпочитает m' мужчине m;

♦ w' предпочитает m мужчине m'.

Что же происходит на этот раз? Предпочтения двух мужчин противоположны (они ставят на первое место разных женщин); то же самое можно сказать и о предпочтениях двух женщин. Однако предпочтения мужчин полностью противоречат предпочтениям женщин.

Во втором примере существуют два разных устойчивых паросочетания. Сочетание, состоящее из пар (m, w) и (m', w'), является устойчивым — оба мужчины довольны, насколько это возможно, и ни один из них не покинет своего партнера. Однако паросочетание из пар (m', w) и (m, w') тоже устойчиво, так как обе женщины довольны, насколько это возможно. Запомните этот важный момент, прежде чем двигаться дальше, — в заданной ситуации может существовать более одного устойчивого паросочетания.

Проектирование алгоритма

Теперь мы продемонстрируем, что для каждого набора списков предпочтений среди мужчин и женщин существует устойчивое паросочетание. Более того, способ демонстрации заодно ответит на второй вопрос, который был задан выше: мы сформулируем эффективный алгоритм, который получает списки предпочтений и строит по ним устойчивое паросочетание.

Рассмотрим некоторые базовые идеи, заложенные в основу алгоритма.

♦ Изначально ни один из участников не имеет пары. Допустим, неженатый мужчина m выбирает женщину w с наивысшей оценкой в его списке предпочтений и делает ей предложение. Можно ли немедленно объявить, что пара (m, w) войдет в итоговое устойчивое паросочетание? Не обязательно; в какой-то момент в будущем мужчина m’, более предпочтительный с точки зрения женщины w, может сделать ей предложение. С другой стороны, для w будет рискованно немедленно отказывать m; она может не получить ни одного предложения от участника с более высокой оценкой в ее списке предпочтений. Таким образом, возникает естественная идея перевести пару (m, w) в промежуточное состояние помолвки.

♦ Допустим, в текущем состоянии некоторые мужчины и женщины свободны (то есть не помолвлены), а другие участвуют в помолвке. Следующий шаг может выглядеть примерно так: произвольный свободный мужчина m выбирает женщину с наивысшей оценкой w, которой он еще не делал предложение, и обращается к ней с предложением. Если женщина w тоже свободна, то m и w вступают в состояние помолвки. В противном случае w уже помолвлена с другим мужчиной m’; тогда она определяет, кто из m и m’ имеет более высокую оценку в ее списке предпочтений; этот мужчина вступает в помолвку с w, а другой становится свободным.

♦ Наконец, алгоритм в какой-то момент должен определить, что ни одного свободного участника не осталось; тогда все помолвки объявляются окончательными и возвращается полученное идеальное паросочетание.

Ниже приводится конкретное описание алгоритма Гейла-Шепли; его промежуточное состояние изображено на рис. 1.2.

Рис. 1.2. Промежуточное состояние алгоритма Гейла-Шепли: свободный мужчина ш делает предложение женщине w

Хотя формулировка алгоритма Гейла-Шепли выглядит достаточно просто, на первый взгляд не очевидно, что он возвращает устойчивое паросочетание — или хотя бы идеальное паросочетание. Сейчас мы докажем устойчивость результата через серию промежуточных фактов.

Анализ алгоритма

Для начала рассмотрим ситуацию с точки зрения женщины w во время выполнения алгоритма. Какое-то время она не получает предложений и остается свободной. Потом мужчина m может сделать ей предложение, и она становится помолвленной. Со временем она может получить дополнительные предложения и принять те из них, в которых повышается оценка ее партнера. Итак, мы приходим к следующим выводам:

(1.1) Женщина w остается помолвленной с момента получения первого предложения; партнеры, с которыми она вступает в помолвку, становятся все лучше и лучше (в контексте ее списка предпочтении).

С точки зрения мужчины ш, во время выполнения алгоритма все происходит иначе. Он остается свободным до тех пор, пока не сделает предложение женщине с наивысшей оценкой в его списке; в этот момент он может вступить в помолвку — а может и не вступить. С течением времени он может переходить из свободного состояния в состояние помолвки и обратно; однако при этом продолжает действовать следующее утверждение.

(1.2) Последовательность женщин, которым m делает предложение, постоянно ухудшается (в контексте его списка предпочтений).

Теперь мы покажем, что алгоритм завершается, и оценим максимальное количество итераций, необходимых для завершения.

(1.3) Алгоритм Гейла-Шепли завершается после выполнения максимум n² итераций цикла “Пока”.

Доказательство. Полезная стратегия определения верхней границы времени выполнения основана на поиске метрики продвижения, а именно: следует найти какую-то точную формулировку того, насколько каждый шаг, выполняемый алгоритмом, приближает его к завершению.

В рассматриваемом алгоритме каждая итерация состоит из предложения, которое некий мужчина делает (не более одного раза) женщине, к которой он еще не обращался ранее. Итак, если обозначить P(t) множество пар (m, w), в которых мужчина m делал предложение w к моменту завершения итерации t, мы видим, что для всех t размер P(t + 1) строго больше размера P(t). Однако всего существует только n² возможных пар, так что за время выполнения алгоритма значение P(*) может возрасти не более n² раз. Следовательно, выполнение алгоритма может потребовать не более n² итераций. ■

В приведенном утверждении и его доказательстве заслуживают внимания два обстоятельства. Во-первых, некоторые выполнения алгоритма (с некоторыми списками предпочтений) могут потребовать около n² итераций, так что анализ достаточно близок к лучшей возможной оценке. Во-вторых, существует много других метрик, которые не так хорошо подходят для оценки продвижения алгоритма, поскольку они не обязательно строго возрастают при каждой итерации. Например, количество свободных участников (а также количество помолвленных пар) может оставаться постоянным между итерациями. Следовательно, эти величины не могут использоваться непосредственно для определения верхней границы максимально возможного количества итераций, как в предыдущем абзаце.

Теперь докажем, что множество S, возвращаемое при завершении алгоритма, действительно является идеальным паросочетанием. Почему это не очевидно? По сути, нужно показать, что ни один мужчина не остановится в конце своего списка предпочтений; выход из цикла возможен только в том случае, если ни одного свободного мужчины не осталось. В этом случае набор помолвленных пар действительно будет идеальным паросочетанием.

Итак, необходимо доказать следующее:

(1.4) Если мужчина m свободен в какой-то точке выполнения алгоритма, то существует женщина, которой он еще не делал предложение.

Доказательство. Предположим, существует точка, в которой мужчина m свободен, но уже сделал предложение всем женщинам. Тогда из (1.1) следует, что каждая из n женщин на этот момент уже помолвлена. Так как набор помолвленных пар образует паросочетание, при этом также должно быть n помолвленных мужчин. Но мужчин всего n, а согласно исходному предположению, mне помолвлен; возникает противоречие. ■

(1.5) Множество S, возвращаемое при завершении, является идеальным паросочетанием.

Доказательство. Множество помолвленных пар всегда образует паросочетание. Предположим, что алгоритм завершается со свободным мужчиной m. При завершении m должен был уже сделать предложение всем женщинам, в противном случае цикл бы не завершился. Но это противоречит положению (1.4), согласно которому не может быть свободного мужчины, который уже сделал предложение всем женщинам. ■

Наконец, мы доказали главное свойство алгоритма, а именно то, что он приводит к устойчивому паросочетанию.

(1.6) Возьмем выполнение алгоритма Гейла-Шепли, возвращающее множество пар S. Это множество S является устойчивым паросочетанием.

Доказательство. Из (1.5) мы уже знаем, что S является идеальным паросочетанием. Таким образом, чтобы доказать, что S является устойчивым паросочетанием, мы предположим, что существует неустойчивость по отношению к S, и придем к противоречию. Согласно приведенному ранее определению, при такой неустойчивости S будет содержать две пары (m, w) и (m', w'), в которых:

♦ m предпочитает w' женщине w;

♦ w' предпочитает m мужчине m'.

В процессе выполнения алгоритма, приведшего к S, последнее предложение m по определению было обращено к w. Вопрос: делал ли m предложение w' в некоторой предшествующей точке выполнения? Если не делал, то женщина w должна находиться в списке предпочтений m выше, чем w', что противоречит нашему допущению о том, что m предпочитает w' женщине w. Если делал, то w' отказала ему ради другого мужчины m'', которого w' предпочитает m. Однако m' является итоговым партнером w', а это значит, что либо m'' = m', либо, согласно (1.1), w' предпочитает своего итогового партнера m' мужчине m''; в любом случае это противоречит предположению о том, что w' предпочитает m мужчине m'.

Следовательно, S является устойчивым паросочетанием. ■

Расширения

Мы начали с определения устойчивого паросочетания и только что доказали, что алгоритм Гейла-Шепли действительно строит его. Теперь будут рассмотрены некоторые дополнительные вопросы относительно поведения алгоритма Гейла-Шепли и его связи со свойствами различных устойчивых паросочетаний.

Прежде всего вернемся к тому, что было продемонстрировано в одном из предыдущих примеров с несколькими устойчивыми паросочетаниями. Вспомните, что списки предпочтений в этом примере выглядели так:

♦ m предпочитает w женщине w';

♦ m’ предпочитает w' женщине w;

♦ w предпочитает m' мужчине m;

♦ w’ предпочитает m мужчине m'.

Теперь при любом выполнении алгоритма Гейла-Шепли m будет помолвлен с w, m' будет помолвлен с w' (возможно, в обратном порядке), и на этом все остановится. Следовательно, другое устойчивое паросочетание, состоящее из пар (m', w) и (m, w'), недостижимо при выполнении алгоритма Гейла-Шепли, в котором мужчины делают предложение. С другой стороны, оно станет достижимым при выполнении версии алгоритма, в которой предложение делают женщины. А в более крупных примерах, в которых с каждой стороны задействовано более двух участников, может существовать еще большее количество возможных устойчивых паросочетаний, многие из которых не могут быть сгенерированы никаким естественным алгоритмом.

Этот пример демонстрирует некоторую “несправедливость” алгоритма Гейла- Шепли, “подыгрывающего” мужчинам. Если предпочтения мужчин идеально распределены (то есть все они ставят на первое место разных женщин), то при любом выполнении алгоритма Гейла-Шепли каждый мужчина окажется в паре со своей главной кандидатурой независимо от предпочтений женщин. Если же предпочтения женщин полностью расходятся с предпочтениями мужчин (как в приведенном примере), то полученное устойчивое паросочетание будет насколько возможно плохим для женщин. Итак, этот простой набор списков предпочтений компактно описывает мир, в котором кому-то суждено оказаться несчастным: женщины несчастны, если предложения делают мужчины, а мужчины несчастны, если предложения делают женщины.

Давайте проанализируем алгоритм Гейла-Шепли более подробно и попробуем понять, насколько общий характер имеет эта “несправедливость”.

Прежде всего, наш пример подчеркивает то обстоятельство, что формулировка алгоритма Гейла-Шепли не является полностью детерминированной: каждый раз, когда имеется свободный мужчина, можно выбрать любого свободного мужчину, который сделает следующее предложение. Различные варианты выбора приводят к разным путям выполнения алгоритма; вот почему в формулировке (1.6) используется осторожное “Возьмем выполнение алгоритма Гейла-Шепли, возвращающее множество пар S”, а не “Возьмем множество пар S, возвращаемое алгоритмом Гейла-Шепли”.

Возникает другой, тоже очень естественный вопрос: приводят ли все выполнения алгоритма Гейла-Шепли к одному паросочетанию? Вопросы такого рода возникают во многих областях теории обработки данных: имеется алгоритм, который работает асинхронно, с множеством независимых компонентов, которые выполняют операции с возможностью сложных взаимодействий. Требуется определить, какую изменчивость вносит такая асинхронность в окончательный результат. Или совершенно другой пример: независимыми компонентами могут быть не мужчины и женщины, а электронные устройства, активизирующие части крыла самолета; последствия асинхронности в их поведении могут быть очень серьезными.

В текущем контексте ответ на этот вопрос оказывается на удивление простым: все выполнения алгоритма Гейла-Шепли приводят к одному паросочетанию. Докажем это утверждение.

Все выполнения приводят к одному паросочетанию

Существует много разных способов доказательства подобных утверждений, нередко требующих довольно сложной аргументации. Как выясняется, самый простой и наиболее содержательный метод заключается в том, чтобы уникальным образом охарактеризовать полученное паросочетание, а потом показать, что все выполнения приводят к паросочетанию, обладающему такой характеристикой.

Что же это за характеристика? Мы покажем, что каждый мужчина в конечном итоге оказывается “лучшим из возможных партнеров” в конкретном смысле. (Вспомните, что это утверждение истинно, если все мужчины предпочитают разных женщин.) Для начала мы будем считать, что женщина w является действительным партнером мужчины m, если существует устойчивое паросочетание, содержащее пару (m, w). Женщина w будет называться лучшим действительным партнером т, если w является действительным партнером т и никакая женщина, которой т назначает более высокую оценку, чем w, не является его действительным партнером. Для обозначения лучшего действительного партнера т будет использоваться запись best(m).

Пусть S* обозначает множество пар {(m, best(m)):m ∈ M}. Докажем следующий факт:

(1.7) Каждое выполнение алгоритма Гейла-Шепли приводит к множеству S*.

Это утверждение выглядит удивительно сразу на нескольких уровнях. Прежде всего, в его текущей формулировке не существует причины полагать, что S* вообще является паросочетанием, не говоря уже об устойчивости. В конце концов, почему у двух мужчин не может быть единого лучшего действительного партнера? Во-вторых, оно фактически заявляет, что алгоритм Гейла-Шепли обеспечивает лучший возможный результат для каждого мужчины одновременно; не существует устойчивого паросочетания, в котором кто-нибудь из мужчин мог бы рассчитывать на более высокий результат. И наконец, оно отвечает на приведенный выше вопрос, показывая, что порядок предложений в алгоритме Гейла-Шепли абсолютно не влияет на конечный результат.

Но, несмотря на все, доказать его не так уж сложно.

Доказательство. Пойдем от обратного: предположим, что некоторое выполнение E алгоритма Гейла-Шепли порождает паросочетание S, в котором некий мужчина находится в одной паре с женщиной, не являющейся его лучшим действительным партнером. Так как мужчины делают предложение в порядке убывания предпочтений, это означает, что он был отвергнут действительным партнером в ходе выполнения E алгоритма. Возьмем первый момент в ходе выполнения E, когда некоторый мужчина (скажем, m) отвергается действительным партнером w. Поскольку мужчины делают предложение по убыванию предпочтений, а предложение отклоняется впервые, неизбежно следует, что женщина w является лучшим действительным партнером m, то есть best(m).

Отказ w мог произойти либо из-за того, что предложение m было отклонено в пользу существующей помолвки w, либо потому, что женщина w разорвала помолвку с m в пользу улучшенного предложения. Но в любом случае в этот момент w образует или продолжает помолвку с мужчиной m', которого она предпочитает m.

Поскольку w является действительным партнером т, должно существовать устойчивое паросочетание S', содержащее пару (m, w). Теперь зададимся вопросом: кто является партнером m' в этом паросочетании? Допустим, это женщина w' ≠ w.

Так как отказ w от предложения т был первым отказом, полученным мужчиной от действительного партнера при выполнении E, из этого следует, что m' не был отвергнут никаким действительным партнером на момент выполнения S, в котором он был помолвлен с w. Поскольку предложения делаются в порядке убывания предпочтений, а w' очевидно является действительным партнером m', из этого следует, что m' предпочитает w женщине w'. Но нам уже известно, что w предпочитает m' мужчине m, поскольку в ходе выполнения E она отвергла m в пользу m'. Так как (m', w) ∉ S’, можно сделать вывод, что пара (m', w) является неустойчивой по отношению к S'.

Но это противоречит требованию об устойчивости S', а следовательно, исходное предположение было неверным. ■

Итак, для мужчин алгоритм Гейла-Шепли идеален. К сожалению, о женщинах того же сказать нельзя. Для женщины w мужчина m является действительным партнером, если существует устойчивое паросочетание, содержащее пару (m, w). Мужчина m будет называться худшим действительным партнером для w, если m является действительным партнером w и ни один мужчина с оценкой ниже, чем m, в списке предпочтений w не является ее действительным партнером.

(1.8) В устойчивом паросочетании S* каждая женщина оказывается в паре со своим худшим действительным партнером.

Доказательство. Предположим, в S* существует пара (m, w), в которой m не является худшим действительным партнером w. Тогда должно существовать устойчивое паросочетание S', в котором w находится в паре с мужчиной m', имеющим более низкую оценку, чем m. В S' мужчина m находится в паре с женщиной w' ≠ w; поскольку w является лучшим действительным партнером m и w' является действительным партнером m, мы видим, что m предпочитает w женщине w'.

Но из сказанного следует, что пара (m, w) является неустойчивой по отношению к S', а это противоречит требованию об устойчивости S', а следовательно, исходное предположение было неверным. ■

Итак, рассмотренный пример, в котором предпочтения мужчин вступали в противоречие с предпочтениями женщин, дает представление о чрезвычайно общем явлении: для любых входных данных сторона, которая делает предложение в алгоритме Гейла-Шепли, оказывается в паре с лучшим из возможных устойчивых партнеров (с ее точки зрения), тогда как сторона, которая не делает предложение, соответственно оказывается с худшим из возможных устойчивых партнеров.