Свертки и быстрое преобразование Фурье - Разделяй и властвуй

В последнем примере этой главы мы покажем, как базовое рекуррентное отношение из (5.1) применяется при разработке алгоритма быстрого преобразования Фурье — алгоритма с широким диапазоном практических применений.

Задача

Даны два вектора a = (a₀, a₁, ..., a_n-1) и b = (b₀, b₁, ..., b_n-1). Существует много стандартных способов их объединения: например, вычисление суммы с получением вектора a + b = (a₀ + b₀, a₁+ b₁, ..., a_n-1 + b_n-1) или вычисление скалярного произведения в форме вещественного числа a ∙ b = a₀b₀ + a₁b₁ + ... + a_n-1b_n-1. (По причинам, которые вскоре станут ясны, векторы в этом разделе удобнее записывать с координатами, которые индексируются с 0, а не с 1.)

Один из способов объединения векторов, находящий очень важные практические применения (хотя и не всегда упоминаемый во вводном курсе линейной алгебры), — свертка a * b. Свертка двух векторов длины n (таких, как a и b) представляет собой вектор с 2n - 1 координатами, в котором координата k равна

Другими словами,

Когда это определение видишь впервые, понять его смысл нелегко. Представьте себе матрицу n х n, в которой элемент (i, j) равен ab:

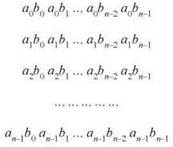
Координаты вектора свертки вычисляются суммированием по диагоналям. Стоит отметить, что, в отличие от векторной суммы и скалярного произведения, свертка легко обобщается на векторы разной длины а = (а₀, а_р ..., a_m-1) и b = (b₀, b₁ ..., b_n-1). В этом более общем случае a * b определяется как вектор с m + n - 1 координатами, в котором координата k равна

И снова можно представить происходящее с помощью матрицы произведений a_ib_j; матрица стала прямоугольной, но координаты по-прежнему могут вычисляться суммированием по диагоналям. (В дальнейшем условие i < m, j < n в сверточном суммировании явно упоминаться не будут, поскольку из контекста понятно, что сумма может вычисляться только по определенным элементам.)

Определение свертки понятно не сразу, но это не все: также не очень понятно, для чего нужна такая операция. В каких обстоятельствах может потребоваться вычисление свертки двух векторов? Однако свертка встречается в множестве самых разнообразных контекстов. Приведем хотя бы несколько примеров.

♦ Первый пример (который также доказывает, что свертка уже встречалась нам в старших классах школы, хотя и неявно) — умножение многочленов. Любой многочлен A(x) = a₀ + a₁x + a₂x² + ... a_m-1x^m-1 может быть естественно представлен в виде вектора коэффициентов a = (a₀, a₁, ..., a_m-1). Теперь для двух многочленов A(x) = a₀ + a₁x + a₂x² + ... a_m-1x^m-1 и B(x) = b₀ + b₁х + b₂х²+ ... b_n-1х^n-1 рассмотрим многочлен C(x) = A(x)B(x), равный их произведению. В многочлене C(x) коэффициент при члене x^k равен

Иначе говоря, вектор коэффициентов C(x) вычисляется как свертка векторов коэффициентов A(x) и B(x).

♦ Пожалуй, самое важное практическое применение сверток лежит в области обработки сигналов. Эта тема сама по себе заслуживает отдельного учебного курса, поэтому мы ограничимся простым примером, который дает общее представление о том, где возникают свертки.

Допустим, имеется вектор a = (a₀, a₁, ..., a_m-1), который представляет серию измерений (температура, данные биржевых котировок и т. д.), зафиксированных в m последовательных временных точках. Такие серии часто содержат высокий уровень шума из-за ошибок измерения или случайных отклонений, поэтому к ним часто применяется операция “сглаживания”: каждое значение a_tусредняется со взвешенной суммой соседей на k позиций слева и справа в последовательности; весовые коэффициенты быстро убывают при увеличении расстояния от a_i. Например, при гауссовом сглаживании a_i заменяется на

с некоторым параметром “ширины” к и значением Z, выбранным просто для нормализации суммы весов в среднем до 1. Существуют некоторые проблемы с граничными условиями (например, что делать, если i - k < 0 или i + k > m?), но они могут решаться игнорированием первых и последних к элементов из сглаженного сигнала или масштабированием по другой схеме, компенсирующей недостающие элементы.

Чтобы понять, как это связано с операцией свертки, можно рассматривать операцию сглаживания следующим образом. Сначала определяется “маска”

состоящая из весов, которые должны использоваться при усреднении каждой точки. (Например, для случая гауссова сглаживания). Затем маска последовательно позиционируется так, чтобы она была совмещена по центру с каждой возможной точкой в серии a; для каждого варианта позиционирования вычисляется взвешенное среднее. Иначе говоря, а_i заменяется на

Последнее выражение фактически является сверткой; чтобы это стало очевидно, нужно лишь немного изменить запись. Определим b = (b₀, b₁, ..., b_2k), где Нетрудно убедиться в том, что с этим определением сглаженное значение вычисляется в виде

Другими словами, сглаженная серия представляет собой результат свертки исходного сигнала и обращенной маски (с некоторыми несуществующими координатами в начале и в конце).

♦ Последний пример — задача объединения гистограмм. Предположим, по результатам социологического опроса были получены две гистограммы: с информацией о ежегодном доходе всех мужчин и женщин в выборке. Нужно построить новую гистограмму, где для каждого k будет отображаться количество пар (M, W), для которых у мужчины M и женщины W суммарный доход составляет k. Задача представляет собой свертку. Первую гистограмму можно записать в виде вектора a = (а₀, ..., a_m-1), который показывает, что существуют а. мужчин с ежегодным доходом, равным i. Аналогичным образом вторая гистограмма записывается в виде вектора b = (b₀, ..., b_n-1). Введем обозначение с_k для количества пар (m, w) с суммарным доходом k; это количество способов, которыми можно выбрать мужчину с доходом а_i и женщину с доходом b_j для любой пары (i, j) с i + j = k. Другими словами,

так что объединенная гистограмма с = (с₀, ..., c_m+n-2) представляет собой простую свертку a и b. (С использованием вероятностной терминологии, которая будет раскрыта в главе 13, этот пример может рассматриваться как применение свертки в качестве способа вычисления распределения суммы двух независимых случайных переменных.)

Вычисление свертки

Разобравшись с тем, для чего нужна свертка, перейдем к задаче ее эффективного вычисления. Для простоты будем рассматривать случай векторов равной длины (то есть m = n), хотя все сказанное может быть напрямую применено к случаю векторов разной длины.

Вычисление свертки — тема более тонкая, чем кажется на первый взгляд. В конце концов, из определения свертки следует абсолютно законный способ ее вычисления: для каждого к вычисляется сумма

а результат используется как значение координаты k. Проблема в том, что при таком прямолинейном способе вычисления свертки приходится вычислять произведение a_ib_j для каждой пары (i, j), а это означает Ө(n²) арифметических операций. Время выполнения O(n²) для вычисления свертки выглядит естественно, так как в определении задействованы O(n²) умножений a_ib_j. Однако неочевидно, что вычисление свертки обязательно должно выполняться за квадратичное время, поскольку и ввод и вывод имеют только размер O(n).

Возможно ли разработать алгоритм, который обходит квадратичный размер определения свертки и вычисляет его другим, более умным способом?

Как ни удивительно, это возможно. Ниже описан метод, который вычисляет свертку двух векторов с использованием только O(n log n) арифметических операций. В его основу заложен эффективный прием, называемый быстрым преобразованием Фурье(Fast Fourier Transform).

Быстрое преобразование Фурье широко применяется для анализа последовательностей числовых значений; быстрое вычисление свертки, которым мы будем заниматься здесь, — всего лишь одно из таких применений.

Разработка и анализ алгоритма

Чтобы преодолеть ограничение квадратичного времени для свертки, мы воспользуемся связью между сверткой и умножением двух многочленов, как в первом из рассмотренных выше примеров. Но вместо того, чтобы использовать свертку как примитив при умножении многочленов, мы будем использовать эту связь в обратном направлении.

Предположим, даны векторы a = (a₀, a₁, ..., a_n-1) и b = (b₀, b₁, ..., b_n-1). Будем рассматривать их как многочлены A(x) = a₀ + a₁x + a₂x² + ... a_n-1x^n-1 и B(x) = b₀ + b₁x + b₂x² + ... b_n-1x^n-1 и посмотрим, как вычислить их произведение C(x) = A(x)B(x) за время O(n log n). Если c = (c₀, c₁, ..., c_2n-2) — вектор коэффициентов C, то, как было сказано выше, c в точности представляет собой свертку a * b, поэтому нужный ответ можно напрямую получить из коэффициентов C(x).

Вместо того чтобы перемножать A и B в алгебраическом виде, мы можем рассматривать их как функции переменной x и перемножим так, как описано ниже.

(i) Сначала выбираем 2n значений x₁, x₂, ..., x_2n и вычисляем A(x_j) и B(x_j) для каждого j = 1, 2, ..., 2n.

(ii) Теперь C(x_j) легко вычисляется для каждого j как произведение двух чисел A(x_j) и B(x_j).

(iii) Остается восстановить C по значениям x₁, x₂, ..., x_2n. Для этого мы воспользуемся одним фундаментальным свойством многочленов: любой многочлен степени d может быть восстановлен по своим значениям для произвольного набора из d + 1 и более точек. Этот механизм, называемый полиномиальной интерполяцией, более подробно рассматривается ниже. А пока заметим, что для многочленов A и B, степень которых не превышает n - 1, степень произведения C не превышает 2n - 2, что позволяет реконструировать многочлен по значениям C(x₁), C(x₂), ..., C(x_2n), вычисленным на шаге (ii).

Этот метод умножения многочленов имеет как положительные аспекты, так и недостатки. Сначала о хорошем: шаг (ii) требует только O(n) арифметических операций, поскольку в нем задействовано умножение O(n) чисел. Но на шагах (i) и (iii) ситуация выглядит уже не столь радужно. В частности, вычисление многочленов A и B для одного значения требует Ω(n) операций, а наш план требует выполнения 2n таких вычислений. Казалось бы, мы снова возвращаемся к квадратичному времени.

Чтобы эта идея заработала, необходимо найти множество из 2n значений x₁, x₂, ..., x_2n, которые связаны определенным образом — например, для которых работа по вычислению A и B может быть повторно использована в разных вычислениях. Множеством, для которого этот способ отлично работает, является множество комплексных корней из единицы.

Комплексные корни из единицы

На этой стадии необходимо вспомнить несколько фактов, касающихся комплексных чисел и их роли в решениях полиномиальных уравнений.

Нам известно, что комплексные числа могут рассматриваться как точки “комплексной плоскости”, оси которой соответствуют действительной и мнимой части числа. Комплексное число записывается в полярных координатах по отношению к этой плоскости в виде re^θi, где е^ωi = -1 (и е^2ωi = 1). Для положительного целого числа k полиномиальное уравнение x^k = 1 имеет к разных комплексных корней, которые легко определяются. Каждое из комплексных чисел ω_j,k = е^2ωji/k (для j = 0, 1, 2, ..., k - 1) удовлетворяет этому уравнению, поскольку

А так как все эти числа различны, то и корни тоже различны. Эти числа называются корнями k-й степени из единицы. Их можно представить как множество из k точек, разделенных одинаковыми расстояниями на единичном круге комплексной

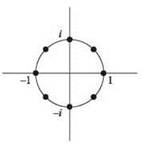
Рис. 5.9. Корни 8-й степени из единицы на комплексной плоскости

Для наших чисел x₁, ..., x_2n, для которых должны вычисляться A и B, мы выберем корни (2n)-Й степени из единицы. Стоит запомнить (хотя это и не обязательно для понимания алгоритма), что использование комплексных корней из единицы лежит в основе самого названия быстрого преобразования Фурье: представление многочлена P степени d его значениями для корней (d + 1)-й степени без единицы иногда называется дискретным преобразованием Фурье для P; “сердцем” нашей процедуры является метод ускорения этих вычислений.

Рекурсивная процедура вычисления многочлена

Мы хотим создать алгоритм рекурсивного вычисления A для каждого из корней (2n)-й степени из единицы, чтобы воспользоваться знакомым рекуррентным отношением из (5.1), а именно T(n) ≤ 2T(n/2) + O(n), где T(n) в данном случае обозначает количество операций, необходимых для вычисления многочлена степени n - 1 для всех корней (2N)-Й степени из единицы. Для простоты при описании алгоритма будем считать, что n является степенью 2.

Как разбить вычисление многочлена на две подзадачи равного размера? Воспользуемся полезным приемом: определим два многочлена A_even(x) и A_odd(x), состоящих из четных и нечетных коэффициентов A соответственно. То есть

и

Простые алгебраические выкладки показывают, что

Итак, в нашем распоряжении появился способ вычисления A(x) с постоянным количеством операций через вычисление двух многочленов, степень каждого из которых равна половине степени A.

Теперь предположим, что каждый из многочленов A_even и A_odd вычисляется для корней n-й степени из единицы. Эта задача в точности соответствует той, с которой мы сталкиваемся для A и корней (2n)-Й степени из единицы, за исключением того, что входные данные уменьшились вдвое: степень равна (n - 2)/2 вместо n - 1, а вместо 2n используются n корней. Следовательно, эти вычисления могут выполняться за время T(n/2) для каждого из многочленов A_even и A_odd, с суммарным временем 2T(n/2).

Мы очень близко подошли к созданию рекурсивного алгоритма, который удовлетворяет условию (5.1) и обеспечивает желаемое время выполнения; остается лишь произвести вычисления A для корней (2n)-Й степени из единицы с использованием O(n) дополнительных операций. Но с учетом результатов рекурсивных вызовов для A_even и A_odd это несложно. Рассмотрим один из этих корней из единицы Величина ω_j,2n² равна а следовательно, ω_j,2n² является корнем n-й степени из единицы. Таким образом, когда мы переходим к вычислениям

выясняется, что оба вычисления в правой части были выполнены на шаге рекурсии и A(ω_j,2n) можно определить с постоянным количеством операций. Таким образом, выполнение этих операций для всех 2n корней из единицы означает O(n) дополнительных операций после двух рекурсивных вызовов, а следовательно, граница T(n) количества операций в самом деле удовлетворяет отношению T(n) ≤ 2T(n/2) + O(n). Та же процедура применяется для вычисления многочлена B для корней (2n)-Й степени из единицы, и это дает желаемую границу O(n log n) для шага (i) нашей структуры алгоритма.

Полиномиальная интерполяция

Мы уже видели, как вычислить A и B для множества всех корней (2n)-Й степени из единицы с использованием O(n log n) операций; и как объясняется выше, произведения вычисляются за O(n) дополнительных операций. Таким образом, для завершения алгоритма умножения A и B необходимо выполнить шаг (iii) приведенной выше схемы с использованием O(n logп) операций для реконструкции C из значений корней (2п)-й степени из единицы.

В описании этой части алгоритма следует иметь в виду один важный момент: как выясняется, задача реконструкции C решается простым определением соответствующего многочлена (см. ниже D) и его вычислением для корней (2n)-й степени из единицы. Только что было показано, как это делается с использованием O(n log n) операций, поэтому мы делаем это снова, выполняя дополнительные O(n log n) операций; это приводит к завершению алгоритма.

Рассмотрим многочлен который нужно реконструировать по значениям C(ω_s,2n) в корнях (2n)-й степени из единицы. Определим новый многочлен где d_s = C(ω_s,2n). Теперь рассмотрим значения D(x) для корней (2n)-й степени из единицы.

по определению. Теперь вспомните, что Используя этот факт и расширяя запись до даже когда s ≥ 2n, мы получаем:

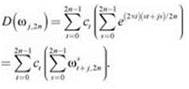
Чтобы проанализировать последнюю строку, мы воспользуемся тем фактом, что для каждого корня (2n)-й степени из единицы ω ≠ 1, имеем Это следует из того, что ω по определению является корнем х²ⁿ - 1= 0; так как и ω ≠ 1, из этого следует, что ш также является корнем

Следовательно, единственная составляющая внешней суммы последней строки, отличная от 0, относится к c_t, для которого ω_t+j,2n = 1; а это происходит, если t + j кратно 2n, то есть если t = 2n - j. Для этого значения Отсюда следует, что Таким образом, вычисление многочлена D(x) в корнях (2n)-й степени из единицы дает коэффициенты многочлена C(x) в обратном порядке (и умноженные на 2n). Подведем итог:

(5.14) Для любого многочлена и соответствующего многочлена выполняется условие

Все вычисления значений D(ω_2n-s,2n) выполняются за O(n log n) операций с использованием метода “разделяй и властвуй”, разработанного для шага (i).

На этом работа подходит к концу: мы реконструировали многочлен C по его значениям для корней (2n)-й степени из единицы, и коэффициенты C определяют координаты искомого вектора свертки c = a * b.

Итак, мы успешно продемонстрировали следующее:

(5.15) Использование быстрого преобразования Фурье для определения произведения многочленов C(x) позволяет вычислить свертку исходных векторов a и b за время O(n log n).