Сегментированные наименьшие квадраты: многовариантный выбор - Динамическое программирование

Перейдем к другой категории задач, которая демонстрирует чуть более сложную разновидность динамического программирования. В предыдущем разделе рекуррентное отношение было разработанно на основе выбора, который был, по сути, бинарным: интервал n либо принадлежал оптимальному решению, либо не принадлежал ему. В задаче, рассматриваемой ниже, в рекуррентности будет задействовано то, что можно назвать “многовариантным выбором”: на каждом шаге существует полиномиальное количество вариантов, которые могут рассматриваться как кандидаты для структуры оптимального решения. Как вы увидите, метод динамического программирования очень естественно адаптируется к этой более общей ситуации.

Отдельно стоит сказать о том, что задача этого раздела также хорошо показывает, как четкое алгоритмическое определение может формализовать понятие, изначально казавшееся слишком нечетким и нелогичным для математического представления.

Задача

При работе с научными и статистическими данными, нанесенными на плоскость, аналитики часто пытаются найти “линию наилучшего соответствия” для этих данных (рис. 6.6).

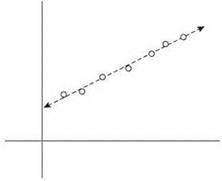
Рис. 6.6. Линия наилучшего соответствия

Эта основополагающая задача из области статистики и вычислительной математики формулируется следующим образом. Допустим, данные представляют собой множество P из n точек на плоскости, обозначаемых (x₁,y₁), (x₂,y₂), ..., (x_n,y_n); предполагается, что x₁ < x₂ < ... < x_n. Для линии L, определяемой уравнением y = ax + b, погрешностью L относительно P называется сумма возведенных в квадрат “расстояний” от точек до P:

Естественной целью в такой ситуации будет нахождение линии с минимальной погрешностью. Оказывается, у этой задачи существует компактное решение, которое легко вычисляется методами математического анализа. Опуская промежуточные выкладки, приведем результат: линия минимальной погрешности определяется формулой y = ax + b, где

Но существует проблема, для которой эти формулы не подойдут. Часто набор данных выглядит примерно так, как показано на рис. 6.7. В таком случае нам хотелось бы сделать утверждение вида “Точки лежат приблизительно на серии из двух линий”. Как формализовать такое понятие?

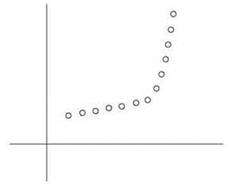
Рис. 6.7. Набор точек, расположенных приблизительно вдоль двух линий

Для любой одиночной линии погрешность у точек на рисунке будет запредельной; но если использовать две линии, ошибка может быть относительно невелика. Итак, новую задачу можно попытаться сформулировать следующим образом: вместо того, чтобы искать одну линию наилучшего соответствия, мы ищем набор линий, обеспечивающий минимальную погрешность. Но такая формулировка задачи никуда не годится, потому что у нее имеется тривиальное решение: при сколь угодно большом наборе линий можно добиться идеального соответствия, соединив линиями каждую пару последовательных точек в P.

С противоположной стороны можно жестко “запрограммировать” число 2 в задаче — искать лучшее соответствие не более чем с двумя линиями. Но и такая формулировка противоречит здравому смыслу: изначально не было никакой априорной информации о том, что точки лежат приблизительно на двух линиях; мы пришли к такому выводу, взглянув на иллюстрацию. Вероятно, большинство людей также скажет, что точки на рис. 6.8 лежат приблизительно на трех линиях.

Рис. 6.8. Набор точек, расположенных приблизительно вдоль трех линий

На интуитивном уровне формулировка задачи должна обеспечивать хорошее прилегание точек с минимально возможным количеством линий. А теперь сформулируем сегментированную задачу наименьших квадратов, которая достаточно четко отражает эти представления. Эта задача является конкретным воплощением более общей проблемы из области анализа данных и статистики, называемой обнаружением изменений: в заданной последовательности точек данных требуется найти несколько точек, в которых происходят дискретные изменения (в нашем случае — переход к другой линейной аппроксимации).

Формулировка задачи

Как и в приведенном выше описании, имеется множество точек P = {(x₁, y₁, (x₂, y₂), ..., (x_n, y_n)}, в котором x₁ < x₂ < ... < x_n. Точка (x, y) будет обозначатьсяp. Сначала необходимо разбить Pна некоторое количество сегментов. Каждый сегмент является подмножеством P, представляющим непрерывный набор координат x; другими словами, это подмножество вида {p_i, p_i+1, ..., p_j-1, p_j} для некоторых индексов i ≤ j. Затем для каждого сегмента S в разбиении P вычисляется линия, минимизирующая погрешность в отношении точек S для приведенных выше формул.

Штраф разбиения определяется как сумма следующих слагаемых:

(i) Количество сегментов, на которые разбивается P, умноженное на фиксированный множитель C > 0.

(ii) Для каждого сегмента — значение погрешности для оптимальной линии через этот сегмент.

Нашей целью в сегментированной задаче наименьших квадратов является нахождение разбиения с минимальным штрафом. Минимизация этой характеристики отражает компромиссы, упоминавшиеся ранее. При поиске решения могут рассматриваться разбиения на любое количество сегментов; с увеличением количества сегментов уменьшаются слагаемые штрафа из части (ii) определения, но увеличивается слагаемое в части (i). (Множитель C предоставляется со входными данными; настраивая C, можно увеличить или уменьшить штраф за использование дополнительных линий.)

Количество возможных разбиений в P растет по экспоненте, и изначально непонятно, возможен ли эффективный поиск оптимального разбиения. Сейчас мы покажем, как использовать динамическое программирование для нахождения минимального штрафа за время, полиномиальное по n.

Разработка алгоритма

Для начала вспомним, какие ингредиенты необходимы для алгоритма динамического программирования (см. в конце раздела 6.2). Это полиномиальное количество подзадач, решения которых должны дать решение исходной задачи; и решения этих подзадач должны строиться с использованием рекуррентного отношения. Как и в случае задачи взвешенного интервального планирования, полезно поразмыслить над некоторыми простыми свойствами оптимального решения. Однако учтите, что прямой аналогии с задачей взвешенного интервального планирования здесь нет: в той задаче мы искали подмножество из n объектов, а здесь ищется способ разбиения n объектов.

Для сегментированной задачи наименьших квадратов очень полезно следующее наблюдение: последняя точка p_n принадлежит одному сегменту оптимального разбиения, и этот сегмент начинается в некоторой более ранней точке р_i. Подобные наблюдения могут подсказать правильное множество подзадач: зная последний сегмент р_i, ..., р_п (рис. 6.9), мы можем исключить эти точки из рассмотрения и рекурсивно решить задачу для оставшихся точек р₁, ..., р_i-1.

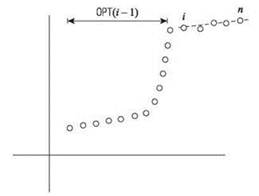
Рис. 6.9. Возможное решение: подбираем один сегмент для точек р_i, р_i+1, ..., р_n, после чего переходим к поиску оптимального решения для оставшихся точек р₁, р₂, ..., р_i-1

Предположим, OPT(z') обозначает оптимальное решение для точек р₁, ..., р_i, а e_i,j — минимальную погрешность для любой линии в отношении р_i, р_i+1, ..., р_j. (Запись OPT(0) = 0 используется как граничный случай.) Тогда приведенное выше наблюдение означает следующее:

(6.6) Если последний сегмент оптимального решения состоит из точек _рi, ..., р_n, то значение оптимального решения равно OPT(n) = e_i,n + C + OPT(i - 1).

Используя то же наблюдение для подзадачи, состоящей из точек р₁, ..., р_j, мы видим, что для получения OPT(j) необходимо найти лучший способ получения завершающего сегмента р_i, ..., р_j — с оплатой погрешности и слагаемого C для этого сегмента — в сочетании с оптимальным решением OPT(i - 1) для остальных точек. Другими словами, мы обосновали следующее рекуррентное отношение:

(6.7) Для подзадачи с точками р₁, ..., р_j

а сегмент р_i, ..., р_j используется в оптимальном решении подзадачи в том и только в том случае, если минимум достигается при использовании индекса i.

Самая сложная часть разработки алгоритма осталась позади. Далее можно просто строить решения OPT(i) в порядке возрастания i.

По аналогии с рассуждениями для взвешенного интервального планирования правильность этого алгоритма напрямую доказывается посредством индукции ((6.7) предоставляет шаг индукции).

Как и в алгоритме взвешенного интервального планирования, оптимальное разбиение вычисляется обратным отслеживанием по M.

Анализ алгоритма

Осталось проанализировать время выполнения Segmented-Least-Squares. Сначала необходимо вычислить значения всех погрешностей наименьших квадратов e_i,j. Чтобы учесть время выполнения, расходуемое на эти вычисления, заметим, что существуют O(n²) пар (i, j), для которых эти вычисления необходимы; для каждой пары (i, j) можно использовать формулу, приведенную в начале этого раздела, для вычисления e за время O(n). Следовательно, общее время выполнения для вычисления всех значений e_i,j равно O(n³).

Алгоритм состоит из n итераций для значений j = 1, ..., n. Для каждого значения j необходимо определить минимум в рекуррентном отношении (6.7) для заполнения элемента массива M[j]; это занимает время O(n) для каждого j, что в сумме дает O(n²). Итак, после определения всех значений e_i,j время выполнения равно O(n²)¹.