Вторичная структура РНК: динамическое программирование по интервалам - Динамическое программирование

В задаче о рюкзаке нам удалось сформулировать алгоритм динамического программирования при добавлении новой переменной. Существует и другой очень распространенный сценарий, в котором в динамическую программу добавляется переменная. Мы начинаем с рассмотрения множества подзадач {1, 2, ..., j} для всех возможных j, но найти естественное рекуррентное отношение не удается. Тогда мы рассматриваем большее множество подзадач из {i, i + 1, ..., j} для всех возможных i и j (где i ≤ j) и находим естественное рекуррентное отношение для этих подзадач. Таким образом, в задачу добавляется вторая переменная i; в результате рассматривается подзадача для каждого непрерывного интервала в {1, 2, ..., n}.

Существует ряд канонических задач, соответствующих этому описанию; читатели, изучавшие алгоритмы разбора для контекстно-независимых грамматик, вероятно, видели хотя бы один алгоритм динамического программирования в этом стиле. А здесь мы сосредоточимся на задаче предсказания вторичной структуры РНК, одной из фундаментальных проблем в области вычислительной биологии.

Задача

Как известно из начального курса биологии, Уотсон и Крик установили, что двухцепочечная ДНК “связывается” комплементарным спариванием оснований. Каждая цепь ДНК может рассматриваться как цепочка оснований, каждое из которых выбирается из множества {A, C, G, T}². Пары образуются как основаниями A и T, так и основаниями C и G; именно связи A-T и C-Gудерживают две цепочки вместе.

Одноцепочечные молекулы РНК являются ключевыми компонентами многих процессов, происходящих в клетках, и строятся по более или менее одинаковым структурным принципам. Однако в отличие от двухцепочечной ДНК, у РНК не существует “второй цепи” для связывания, поэтому РНК обычно образует пары оснований сама с собой; это приводит к образованию интересных форм наподобие изображенной на рис. 6.13. Совокупности пар (и полученная форма), образованные молекулой РНК в этом процессе, называются вторичной структурой; понимание вторичной структуры необходимо для понимания поведения молекулы.

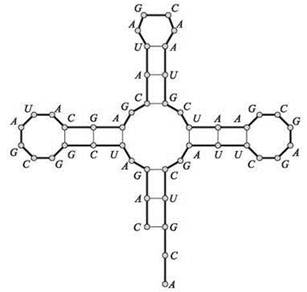
Рис. 6.13. Вторичная структура РНК. Жирными линиями обозначаются смежные элементы последовательности, а тонкими — элементы, образующие пары

Для наших целей одноцепочечная молекула РНК может рассматриваться как последовательность из n символов (оснований) алфавита {A, C, G, U}³. Пусть B = b₁b₂... b_n — одноцепочечная молекула РНК, в которой все b_i ∈ {A, C, G, U}. В первом приближении вторичная структура может моделироваться следующим образом. Как обычно, основание A образует пары с U, а основание C образует пары с G; также требуется, чтобы каждое основание могло образовать пару с не более чем одним другим основанием, иначе говоря, множество пар оснований образует паросочетание. Также вторичные структуры (снова в первом приближении) не образуют узлов, что ниже формально определяется как своего рода условие отсутствия пересечений.

А если более конкретно, вторичная структура B представляет собой множество пар S = {(i, j)}, где i, j ∈ {1, 2, ..., n}, удовлетворяющих следующим условиям:

(i) (Отсутствие крутых поворотов) Концы каждой пары в S разделяются минимум четырьмя промежуточными основаниями; иначе говоря, если (i, j) ∈ S, то i < j - 4.

(ii) Любая пара в S состоит из элементов {A, U} или {C, G} (в произвольном порядке).

(iii) S является паросочетанием; никакое основание не входит более чем в одну пару.

(iv) (Отсутствие пересечений) Если (i, j) и (k, l) — две пары в S, то невозможна ситуация i < к < j < l (рис. 6.14).

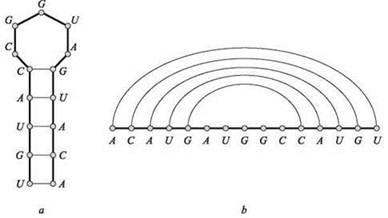
Рис. 6.14. Два представления вторичной структуры РНК. Во втором представлении (b) цепочка “вытянута в длину”, а отрезки, соединяющие пары, выглядят как непересекающиеся “купола” над цепочкой

Вторичная структура РНК на рис. 6.13 удовлетворяет свойствам (i)-(iv). Со структурной точки зрения условие (i) выполняется просто из-за того, что молекула РНК не может слишком резко изгибаться, а условия (ii) и (iii) определяются фундаментальными правилами сочетания оснований Уотсона-Крика. С условием (iv) дело обстоит сложнее: непонятно, почему оно должно выполняться в природе. Но хотя в реальных молекулах встречаются отдельные исключения (так называемые псевдоузлы), как выясняется, это ограничение хорошо аппроксимирует пространственные ограничения реальных вторичных структур РНК.

Итак, из всего множества вторичных структур, возможных для одной молекулы РНК, какие конфигурации могут возникнуть в физиологических условиях? Обычно предполагается, что одноцепочечная молекула РНК образует вторичную структуру с оптимальной общей свободной энергией. На тему правильной модели свободной энергии вторичной структуры идут ожесточенные споры; но мы будем в первом приближении считать, что свободная энергия вторичной структуры пропорциональна количеству содержащихся в ней пар оснований.

После всего сказанного базовая задача предсказания вторичной структуры РНК формулируется очень просто: требуется найти эффективный алгоритм, который получает одноцепочечную молекулу РНК B = b₁b₂... b_n и определяет вторичную структуру S с максимально возможным количеством пар оснований.

Разработка и анализ алгоритма

Динамическое программирование: первая попытка

Вероятно, первая естественная попытка применения динамического программирования будет основана на следующих подзадачах: мы говорим, что OPT(j) — максимальное количество пар оснований во вторичной структуре b₁, b₂, ..., b_j. Согласно приведенному выше запрету на резкие повороты, мы знаем, что OPT(j) = 0 для j ≤ 5; также известно, что OPT(n) — искомое решение.

Проблемы начинаются тогда, когда мы пытаемся записать рекуррентное отношение, выражающее OPT(j) в контексте решений меньших подзадач. Здесь можно пройти часть пути: в оптимальной вторичной структуре b₁, b₂, ..., b_j возможно одно из двух:

♦ j не участвует в паре; или

♦ j участвует в паре с t для некоторого t < j - 4.

В первом случае необходимо обратиться к решению для OPT(j - 1). Второй случай изображен на рис. 6.15, а; из-за запрета на пересечения мы знаем, что не может существовать пары, один конец которой находится между 1 и t - 1, а другой — между t + 1 и j - 1. Таким образом, мы фактически выделили две новые подзадачи: для оснований b₁b₂ ... b_t-1 и для оснований b_t+1 ... b_j-1. Первая решается как OPT(t - 1), а вторая в наш список подзадач не входит, потому что она не начинается с b₁.

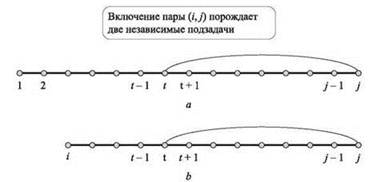
Рис. 6.15. Схематическое представление рекуррентности динамического программирования с использованием (а) одной переменной, (b) двух переменных

Это соображение наводит на мысль о том, что в задачу следует добавить переменную. Нужно иметь возможность работать с подзадачами, не начинающимися с b₁; другими словами, необходимо иметь возможность рассматривать подзадачи для b_ib_i+1 ... b_j при любых i ≤ j.

Динамическое программирование по интервалам

После принятия этого решения приведенные выше рассуждения ведут прямо к успешной рекурсии. Пусть OPT(i, j) — максимальное количество пар оснований во вторичной структуре b_ib_i+1 ... b_j. Запрет на резкие повороты позволяет инициализировать OPT(i, j) = 0 для всех i ≥ j - 4.

(Для удобства записи мы также разрешим ссылки OPT(i, j) даже при i > j; в этом случае значение равно 0).

Теперь в оптимальной вторичной структуре b_ib_i+1 ... b_j существуют те же альтернативы, что и прежде:

♦ j не участвует в паре; или

♦ j находится в паре с t для некоторого t < j - 4.

В первом случае имеем OPT(i, j) = OPT(i, j - 1). Во втором случае, изображенном на рис. 6.15, b, порождаются две подзадачи OPT(i, t - 1) и OPT(t + 1, j - 1); как было показано выше, эти две задачи изолируются друг от друга условием отсутствия пересечений.

Следовательно, мы только что обосновали следующее рекуррентное отношение:

(6.13) OPT(i, j) = max(OPT(i, j - 1), max(1 + OPT(i, t - 1) + OPT(t + 1, j - 1))), где max определяется по t, для которых b_t и b_j образуют допустимую пару оснований (с учетом условий (i) и (ii) из определения вторичной структуры).

Теперь нужно убедиться в правильном понимании порядка построения решений подзадач. Из (6.13) видно, что решения подзадач всегда вызываются для более коротких интервалов: тех, для которых k = j - i меньше. Следовательно, схема будет работать без каких-либо проблем, если решения строятся в порядке возрастания длин интервалов.

Рассмотрим пример выполнения этого алгоритма для входных данных ACCGGUAGU (рис. 6.14). Как и в задаче о рюкзаке, для представления массива M понадобятся два массива: для левой и для правой конечных точек рассматриваемого интервала. На рисунке представлены только элементы, соответствующие парам [i, j] с i < j - 4, потому что только они могут быть отличны от нуля.

Рис. 6.16. Итерации алгоритма для конкретного экземпляра задачи предсказания вторичной структуры РНК

Найти границу для времени выполнения несложно: существуют O(n²) подзадач, которые необходимо решить, а вычисление рекуррентного отношения в (6.13) занимает время O(n) для каждой задачи. Следовательно, время выполнения будет равно O(n³).

Как обычно, саму вторичную структуру (а не только ее значение) можно восстановить сохранением информации о достижении минимума в (6.13) и обратного отслеживания по вычислениям.