Алгоритмы - Разработка и применение - 2016 год
Упражнения с решениями - Урок 6 - Динамическое программирование
Упражнение с решением 1
Вы управляете строительством рекламных щитов на дороге с интенсивным движением, идущей с запада на восток на протяжении M миль. Возможные точки для установки рекламных щитов определяются числами x1, x2, ..., xn, каждое из которых принадлежит интервалу [0, M] (эти числа определяют позицию в милях от западного конца дороги). Разместив рекламный щит в точке х, вы получите прибыль ri > 0.
По правилам дорожной службы округа два рекламных щита не могут находиться на расстоянии 5 миль и менее. Требуется разместить рекламные щиты на подмножестве точек так, чтобы обеспечить максимальную прибыль с учетом ограничения.
Пример. Предположим, M = 20, n = 4, {x1, x2, x3, x4} = {6, 7, 12, 14}, и {r1, r2, r3, r4} = = {5, 6, 5, 1}. В оптимальном решении рекламные щиты размещаются в точках x1 и x3, с суммарной прибылью 10.
Предложите алгоритм, который получает экземпляр этой задачи и возвращает максимальную суммарную прибыль, которая может быть получена для любого действительного подмножества точек. Время выполнения алгоритма должно быть полиномиальным по n.
Решение
Следующие рассуждения позволяют естественным образом применить к этой задаче принцип динамического программирования. Рассмотрим оптимальное решение для заданного входного экземпляра задачи; в этом решении рекламный щит либо размещается в точке xn, либо не размещается. Если щит не размещается, то оптимальное решение для точек x1, ..., xn совпадает с оптимальным решением для точек x1, ..., xn-1; если же щит размещается, следует исключить xn и все остальные точки на расстоянии до 5 миль включительно и найти оптимальное решение для полученного множества. Аналогичные рассуждения применимы при рассмотрении задачи, определяемой только первыми j сайтами x1, ..., xj: точка xj либо включается в оптимальное решение, либо не включается с теми же последствиями.
Определим вспомогательные обозначения, которые помогут выразить эту идею. Для точки xj величина e(j) обозначает крайнюю точку на восточном направлении, которая удалена от xj не более чем на 5 миль. Так как точки нумеруются с запада на восток, это означает, что допустимыми вариантами после решения о размещении рекламного щита в точке хj остаются точки x1, x2, ..., xe(j), но не точки xe(j)+1, ..., xj-1.
Теперь из приведенных выше рассуждений вытекает следующее рекуррентное отношение. Если обозначить OPT(j) доход от оптимального подмножества точек из x1, ..., xj, имеем
![]()
Итак, мы собрали основные ингредиенты, необходимых для работы алгоритма динамического программирования. Во-первых, это множество из n подзадач, состоящее из первых j точек для j = 0, 1, 2, ..., n. Во-вторых, имеется рекуррентное отношение ![]() которое позволяет строить решения подзадач.
которое позволяет строить решения подзадач.
Чтобы преобразовать все это в алгоритм, достаточно определить массив M, в котором будут храниться значения OPT, и сформировать на основе рекуррентного отношения цикл, который строит значения M[j] в порядке возрастания j.
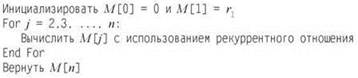
Как и во всех алгоритмах динамического программирования, представленных в этой главе, оптимальное множество рекламных щитов строится обратным отслеживанием по значениям массива M.
При заданных значениях e(j) для всех j время выполнения алгоритма составляет O(n), потому что каждая итерация цикла выполняется за постоянное время. Мы также можем вычислить все значения e(j) за время O(n): для каждой точки xt определяется x'i = xi - 5. Затем отсортированный список x1, ..., xn объединяется с отсортированным списком x'1, ..., x'n за линейное время, как было показано в главе 2. Теперь мы перебираем элементы объединенного списка; добравшись до элемента x'j, мы знаем, что все последующие элементы до xj не могут быть выбраны вместе с xj(потому что находятся на расстоянии менее 5 миль), поэтому мы просто определяем e(j) как наибольшее значение i, для которого мы обнаружили xi при переборе.
И последнее замечание по поводу этой задачи. Очевидно, решение очень похоже на решение задачи взвешенного интервального планирования, и для этого существует веская причина. Дело в том, что задача размещения рекламных щитов может быть напрямую сформулирована как экземпляр задачи взвешенного интервального планирования. Предположим, для каждой точки x. определяется интервал с конечными точками [xi - 5, xi] и вес ri. Затем для любого неперекрывающегося множества интервалов соответствующее множество точек обладает тем свойством, что никакие две точки не могут находиться на расстоянии менее 5 миль. Соответственно, для любого такого множества точек (никакие две на расстоянии менее 5 миль) интервалы, связанные с ними, не будут перекрываться. Следовательно, группы неперекрывающихся интервалов точно соответствуют множеству действительных размещений рекламных щитов, а подстановка только что определенного нами множества интервалов (с их весами) в алгоритм взвешенного интервального планирования даст желаемое решение.
Упражнение с решением 2
Вас приглашают для проведения консультаций в компанию Clones ‘R' Us (CRU), специализирующуюся на передовых исследованиях в области биотехнологий. Поначалу вы не уверены в том, что ваш опыт решения алгоритмических задач пригодится в такой области, но вскоре вы общаетесь с двумя подозрительно похожими инженерами, ломающими голову над нетривиальной задачей.
Эта задача основана на конкатенации последовательностей генетических материалов. Если X и Y — строки с фиксированным алфавитом S, то запись XY обозначает строку, полученную в результате их конкатенации: содержимое X, за которым следует содержимое Y. Ученые выявили целевую последовательность A генетического материала, состоящую из m символов, и они хотят построить последовательность, как можно более близкую к A. Для этого была сформирована библиотека С, состоящая из k (более коротких) последовательностей, длина каждой из которых не превышает n. Ученые могут легко воспроизвести любую последовательность, состоящую из сцепленных копий строк из С (с возможными повторениями).
Конкатенацией по L называется любая последовательность в форме B1B2... Bl, в которой каждый элемент Bi принадлежит множеству L. (Еще раз: повторения разрешены, так что Bi и Bj могут соответствовать одной строке в С для разных значений i и j). Требуется найти конкатенацию по {Bi}, для которой стоимость выравнивания последовательностей будет минимальной. (Для вычисления стоимости выравнивания последовательностей можно считать, что вам даны стоимости разрыва δ и несоответствия αpq для каждой пары p, q ∈ S.)
Предложите алгоритм с полиномиальным временем для этой задачи.
Решение
Эта задача отдаленно напоминает сегментированную задачу наименьших квадратов: имеется длинная последовательность “данных” (строка A), которую требуется “аппроксимировать” более короткими сегментами (строки из L).
Если бы мы хотели развить эту аналогию, решение можно было бы искать следующим образом. Пусть B = B1B2... Bl — конкатенация по L, которая как можно лучше совмещается с заданной строкой A. (Иначе говоря, B является оптимальным решением для входного экземпляра.) Рассмотрим оптимальное выравнивание M строки A с B; t — первая позиция в A, сопоставленная с некоторым символом в Bl, а Al — подстрока A от позиции t до конца. (Иллюстрация для l = 3 приведена на рис. 6.27.) В этом оптимальном выравнивании M подстрока Al оптимально выравнивается с Bl; действительно, если бы существовал лучший способ выравнивания Al с Bl, мы могли бы подставить его в ту часть M, в которой Al выравнивается с Bl, и улучшить общее выравнивание A с B.

Рис. 6.27. В оптимальной конкатенации строк для выравнивания с A существует завершающая строка (B3 на схеме), выравниваемая с подстрокой A (A3 на схеме), которая проходит от позиции t до конца
Отсюда можно сделать вывод, что поиск оптимального решения может вестись следующим образом. Существует некий завершающий фрагмент Al, выровненный с одной из строк в С, и для этого фрагмента мы просто находим строку в L, которая выравнивается с ним настолько хорошо, насколько это возможно. После обнаружения оптимального выравнивания для Al этот фрагмент можно отделить и продолжить поиск оптимального решения для остатка A.
Такой подход к решению задачи ничего не говорит о том, как именно следует продолжать: мы не знаем, какую длину должен иметь фрагмент Al или с какой строкой из L он должен совмещаться. Тем не менее такие характеристики определяются алгоритмами динамического программирования. Фактически ситуация выглядит так же, как в сегментированной задаче наименьших квадратов: тогда мы знали, что должны прерваться где-то в последовательности входных точек, как можно лучше аппроксимировать их одной линией, а затем продолжить с остальными входными точками.
Итак, подготовим все необходимое для того, чтобы сделать возможным поиск Al. Пусть A[x : у] — подстрока A, состоящая из символов от позиции x до позиции у включительно, а c(x, у) — стоимость оптимального выравнивания A[x : у] с любой строкой из L (иначе говоря, мы перебираем все строки из L и находим ту, которая лучше всего выравнивается с A[x : у]). Пусть OPT(j) обозначает стоимость выравнивания оптимального решения для строки A[1 : j].
Из приведенных выше рассуждений следует, что оптимальное решение для A[1 : j] складывается из выявления итоговой “границы сегмента” t < j, нахождения оптимального выравнивания A[t: j] с одной строкой в L и итеративного выполнения для A[1 : t - 1]. Стоимость этого выравнивания для A[t : j] равна c(t, j), а стоимость выравнивания с остатком — OPT(t - 1). Это наводит на мысль о том, что подзадачи хорошо сочетаются друг с другом, и обосновывает следующее рекуррентное отношение.
(6.37) OPT(j) = mint < jc(t, j) + OPT(t - 1) для j ≥ 1, и OPT(0) = 0.
Полный алгоритм состоит из вычисления величин c(t, j) для t < j и последующего построения значений OPT(j) в порядке возрастания j. Эти значения хранятся в массиве M.

Как обычно, мы можем получить конкатенацию, достигающую этой цели, обратным отслеживанием по массиву значений OPT.
Рассмотрим время выполнения алгоритма. Во-первых, всего требуется вычислить O(m2) значений c(t, j). Для каждого из них нужно проверить каждую из к строк B ∈ L и вычислить оптимальное выравнивание B с A[t : j] за время O(n(j - t)) = O(mn). Следовательно, общее время вычисления всех значений c(t, j) составляет O(km3n).
Этот фактор доминирует над временем вычисления всех значений OPT: вычисление OPT(j) использует рекуррентное отношение в (6.37), а это требует времени O(m) для вычисления минимума. Суммируя по всем вариантам j = 1, 2, ..., m, мы получаем время O(m2) для этой части алгоритма.
Упражнения
1. Имеется ненаправленный граф с n узлами G = (V, E). Напомним, что подмножество узлов называется независимым множеством, если никакие два узла не соединяются ребром. В общем виде задача нахождения большого независимого множества сложна, но при достаточно “простом” графе она имеет эффективное решение.
Назовем граф G = (V, E) путевым графом, если его узлы могут быть записаны в виде v1, v2, ..., vn, причем vi и vj соединяются ребром в том и только в том случае, если i и j различаются ровно на 1. С каждым узлом vi связывается положительный целый вес wi.
Для примера рассмотрим путевой граф из пяти узлов на рис. 6.28. Веса обозначены числами внутри узлов.
![]()
Рис. 6.28. Путевой граф с весами, обозначенными на узлах. Максимальный вес независимого множества равен 14
Целью этого упражнения является решение следующей задачи:
Найдите в путевом графе G независимое множество с максимальным общим весом.
(a) Приведите пример, показывающий, что следующий алгоритм не всегда находит независимое множество с максимальным общим весом.

(b) Приведите пример, показывающий что следующий алгоритм тоже не всегда находит независимое множество с максимальным общим весом.

(c) Предложите алгоритм, который получает путевой граф G из n узлов с весами и возвращает независимое множество с максимальным общим весом. Время выполнения должно быть полиномиальным по n независимо от значений весов.
2. Предположим, вы руководите рабочей группой, состоящей из опытных хакеров, и каждую неделю выбираете для них задание. Задания делятся на некритичные (например, создание сайта для класса в местной начальной школе) и критичные (защита важнейших национальных секретов или помощь группе студентов Корнельского университета в разработке компилятора). Каждую неделю приходится принимать решение: какое задание взять, критичное или некритичное?
При выборе некритичного задания в неделю i вы получаете доход li > 0 долларов; при выборе критичного задания доход составит hi > 0 долларов. Проблема в том, что группа может взять критичное задание в неделю i только в том случае, если в неделю i - 1 она не выполняла вообще никакого задания (критичного или некритичного); для такой ответственной работы необходима целая неделя подготовки. С другой стороны, если группа выполняла задание (любого типа) в неделю i - 1, ничто не помешает ей выполнить некритичное задание в неделю i. Итак, для заданной последовательности из n недель план задается выбором “некритичное задание”, “критичное задание” или “нет задания” для каждой из n недель с тем свойством, что при выборе “критичное задание” для недели i > 1 в неделе i - 1 должно быть выбрано задание i - 1. (Допускается выбор критичного задания в неделю 1.) Значение плана определяется следующим образом: для каждого i значение увеличивается на /, если в неделю i было выбрано “некритичное задание”, и значение увеличивается на h, если в неделю i было выбрано “критичное задание”. (Если в неделю i не было выбрано никакое задание, значение увеличивается на 0.)
Задача. Для заданных множеств значений l1, l2, ..., ln и h1, h2, ..., hn найти план с максимальным значением (такой план будет называться оптимальным).
Пример. Допустим, n = 4, а значения li и hi задаются следующей таблицей. В этом случае план с максимальным значением достигается выбором “нет задания” в неделю 1, выбором критичного задания в неделю 2 и выбором некритичного задания в недели 3 и 4. Значение такого плана составит 0 + 50 + 10 + 10 = 70.
|
Неделя 1 |
Неделя 2 |
Неделя 3 |
Неделя 4 |
|
|
l |
10 |
1 |
10 |
10 |
|
h |
5 |
50 |
5 |
1 |
(а) Покажите, что следующий алгоритм не дает правильного решения этой задачи; для этого предложите экземпляр задачи, для которого алгоритм возвращает неправильный ответ.


Чтобы избежать проблем с выходом за границу массива, определим hi = li = 0 при i > n.
Также приведите правильный алгоритм и укажите, какой результат находит приведенный алгоритм.
(b) Предложите эффективный алгоритм, который получает значения l1, l2, ..., ln и h1, h2, ..., hn и возвращает значение оптимального плана.
3. Имеется направленный граф G = (V, E) с узлами v1, ..., vn. Граф G называется упорядоченным, если он обладает следующими свойствами:
(i) каждое ребро идет от узла с меньшим индексом к узлу с большим индексом. Иначе говоря, каждое направленное ребро имеет форму (vi, vj) c i < j;
(ii) из каждого узла, кроме vn, выходит минимум одно ребро, то есть для каждого узла vi с i = 1, 2, ..., n - 1 существует минимум одно ребро в форме (vi, vj).
Длина пути определяется количеством ребер, входящих в этот путь. В этом упражнении решается следующая задача (пример представлен на рис. 6.29):
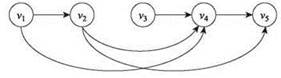
Рис. 6.29. Правильный ответ для этого упорядоченного графа равен 3: самый длинный путь из v1 в vn состоит из трех ребер (v1,v2),(v2,v4) и (v4,v5)
Для заданного графа G найдите длину самого длинного пути, который начинается в v1 и заканчивается в vn.
(a) Покажите, что следующий алгоритм не дает правильного решения этой задачи; для этого приведите пример упорядоченного графа, для которого алгоритм возвращает неправильный ответ.

В своем примере укажите правильный ответ и объясните, какой результат находит приведенный алгоритм.
(b) Предложите эффективный алгоритм, который получает упорядоченный граф G и возвращает длину самого длинного пути, который начинается в v1 и заканчивается в vn. (Еще раз: под длиной понимается количество ребер в пути.)
4. Вы руководите небольшой фирмой — вы, двое сотрудников и арендованная техника. Ваши клиенты распределены между Восточным и Западным побережьем. В каждом месяце вы можете вести дела из офиса в Нью-Йорке (NY) или из офиса в Сан-Франциско (SF). В месяце i текущие издержки составляют N, если дела ведутся из Нью-Йорка, или S, если дела ведутся из Сан-Франциско (величина зависит от потребностей клиентов в этом месяце).
Но если в месяце i вы ведете дела из одного города, а в месяце i + 1 — из другого города, затраты на перемещение составляют фиксированную величину M.
Для заданной последовательности из n месяцев план представляет собой серию из n вариантов местонахождения (NY или SF); i-й элемент последовательности обозначает город, в котором вы будете вести дела в i-м месяце. Стоимость плана определяется как сумма текущих издержек для каждого из n месяцев и затрат M для каждого перемещения между городами. План может начинаться с любого города.
Задача. Для заданной стоимости перемещения M и последовательностей текущих издержек N1, ..., Nn и S1, ..., Sn найдите план с минимальной стоимостью (назовем такой план оптимальным).
Пример. Допустим, n = 4, M = 10, а текущие издержки задаются следующей таблицей.
|
Месяц 1 |
Месяц 2 |
Месяц 3 |
Месяц 4 |
|
|
NY |
1 |
3 |
20 |
30 |
|
SF |
50 |
20 |
2 |
4 |
В этом случае план с минимальной стоимостью будет представлять собой последовательность [NY, NY, SF, SF] с общей стоимостью 1 + 3 + 2 + 4 + 10 = 20 (последнее слагаемое 10 появляется из-за однократного перемещения).
(а) Покажите, что следующий алгоритм не дает правильного решения этой задачи; для этого приведите пример экземпляра задачи, для которого алгоритм возвращает неправильный ответ.

В своем примере укажите правильный ответ и объясните, какой результат находит приведенный алгоритм.
(b) Приведите пример, в котором каждый оптимальный план требует не менее трех перемещений между городами.
Кратко объясните, почему ваш пример обладает таким свойством.
(c) Предложите эффективный алгоритм, который получает значения n, M и последовательности текущих издержек N1, ..., Nn и S1, ..., Sn и возвращает стоимость оптимального плана.
5. Как вам, вероятно, известно, в некоторых языках (включая китайский и японский) слова не разделяются пробелами. По этой причине программы, работающие с текстом, написанным на этих языках, должны решать проблему сегментации слов, то есть вычисления вероятных границ между смежными словами в тексте. Представьте, что английский текст записывается без пробелов; вы получаете строку вида “meetateight” и решаете, что лучшим разбиением будет “meet at eight” (а не “me et at eight”, “meet ateight” или какой-нибудь менее вероятный вариант). Как автоматизировать этот процесс?
Простой, но достаточно эффективный метод основан на поиске сегментации, которая максимизирует накапливаемое “качество” отдельных составляющих слов. Допустим, у вас есть “черный ящик”, который для любой цепочки букв x = x1x2 ... xk возвращает число quality(x). Это число может быть, как положительным, так и отрицательным; большие числа соответствуют более вероятным английским словам. (Значение quality("me") будет положительным, тогда как значение quality("ght") будет отрицательным).
Для длинной цепочки букв y = y1y2... yn сегментация у представляет собой вариант разбиения последовательности на непрерывные блоки букв; каждый блок соответствует одному слову в сегментации. Общее качество сегментации вычисляется суммированием качества каждого блока. (Таким образом, правильный ответ для приводившейся выше строки будет получен при условии, что сумма quality("meet")+quality("at")+quality("eight") больше суммы любой другой сегментации строки.)
Предложите эффективный алгоритм, который получает строку y и вычисляет сегментацию с максимальным общим качеством. (Одно обращение к “черному ящику” для вычисления quality(x) считается одним вычислительным шагом.) (Последнее замечание, не обязательное для решения задачи: для повышения быстродействия программы сегментации на практике используют более сложную формулировку задачи: например, предполагается, что решение не только должно быть разумным на уровне слов, но и образовывать связные обороты и предложения. Например, строку “theyouthevent” можно как минимум тремя способами разбить на обычные английские слова, но один из вариантов дает намного более осмысленную фразу, чем два других. Если рассматривать происходящее в терминологии формальных языков, расширенная задача напоминает поиск сегментации, которая также хорошо разбирается в соответствии с грамматикой используемого языка. Но даже с этими дополнительными критериями и ограничениями в основе многих эффективных систем сегментации лежат методы динамического программирования.)
6. При форматировании текста часто встречается стандартная задача: взять текст с “рваным” правым краем:

и преобразовать его в текст, правый край которого “сглажен”, насколько это возможно:

Чтобы формализовать эту задачу и начать размышлять над реализацией, сначала нужно определить, что же понимать под “сглаженным” правым краем. Допустим, текст состоит из последовательности слов W = {w1, w2, ..., wn}, а слово w состоит из с. символов. Максимальная длина строки равна L. Будем считать, что при выводе используется моноширинный шрифт, а знаки препинания и переносы не учитываются.
Форматирование W состоит из разбиения слов W на строки. В словах, назначенных одной строке, после каждого слова, кроме последнего, должен следовать пробел; соответственно если слова wj, wj+1, ..., wk назначены в одну строку, должно выполняться условие
![]()
Назовем назначение слов по строкам действительным, если оно удовлетворяет этому неравенству. Разность между левой и правой частью будет называться допуском строки (она равна количеству пробелов у правого края).
Предложите эффективный алгоритм для разбиения множества слов W на действительные строки, чтобы сумма квадратов допусков всех строк (включая последнюю) была минимальной.
7. В одном из упражнений с решениями главы 5 представлен алгоритм с временем выполнения O(n log n) для следующей задачи. Рассматриваются цены акций за n последовательных дней, пронумерованных i = 1, 2, ..., n. Для каждого дня i известна биржевая котировка этих акций p(i) в этот день. (Для простоты будем считать, что в течение дня котировка не изменяется.) Вопрос: как выбрать день i для покупки акций и последующий день j для их продажи, чтобы получить максимальную прибыль p(j)-p(i)? (Если за эти n дней перепродажа с прибылью невозможна, алгоритм должен сообщить об этом.)
В приведенном решении показано, как найти оптимальную пару дней i и j за время O(n log n). Однако на самом деле можно найти еще более эффективный алгоритм. Покажите, как найти оптимальные числа i и j за время O(n).
8. Обитатели подземного города Зиона для защиты от нападающих машин применяют кунг-фу, тяжелую артиллерию и эффективные алгоритмы. Недавно они заинтересовались автоматизированными средствами отражения атак.
Вот как проходит типичная атака:
• Рой машин прибывает в течение n секунд; на i-й секунде появляются xt роботов. Благодаря системе раннего оповещения последовательность x1, x2, ..., xn известна заранее.
• В вашем распоряжении имеется электромагнитная пушка (ЭМП), которая может уничтожить часть роботов при появлении; мощность выстрела зависит от того, сколько времени заряжалась пушка. Или в более точной формулировке: имеется такая функция f(∙), что по прошествии j секунд с момента последнего выстрела ЭМП может уничтожить до f(j) роботов.
• Итак, если пушка использовалась на к-й секунде и с момента последнего выстрела прошло j секунд, она может уничтожить min(xk,f(j)) роботов. (После использования пушка полностью разряжается).
• Также будем считать, что в исходном состоянии ЭМП полностью разряжена, поэтому если она впервые используется на j-й секунде, она может уничтожить до f(j) роботов.
Задача. Для заданной последовательности прибытия роботов x1, x2, ..., xn, и функции перезарядки f(∙) выберите моменты времени, в которые следует активировать ЭМП для уничтожения максимального количества роботов.
Пример. Допустим, n = 4, а значения xi и f(i) задаются следующей таблицей.
|
i |
1 |
2 |
3 |
4 |
|
xi |
1 |
10 |
10 |
1 |
|
f(i) |
1 |
2 |
4 |
8 |
В оптимальном решении ЭМП активируется на 3 и 4 секундах. На 3 секунде ЭМП прошла 3-секундную зарядку и поэтому уничтожает min(10,4) = 4 роботов; на 4 секунде с момента последнего выстрела прошла всего 1 секунда, поэтому уничтожается min(1,1) = 1 робот. В сумме получается 5.
(а) Покажите, что следующий алгоритм не дает правильного решения этой задачи; для этого приведите пример экземпляра задачи, для которого алгоритм возвращает неправильный ответ.

В своем примере укажите правильный ответ и объясните, какой результат находит приведенный алгоритм.
(b) Предложите эффективный алгоритм, который получает план прибытия роботов x1, x2, ..., xn и функцию перезарядки f(∙) и возвращает максимальное количество роботов, которые могут быть уничтожены серией активаций ЭМП.
9. Вы участвуете в администрировании высокопроизводительной компьютерной системы, способной обрабатывать несколько терабайт данных в день. В каждый из n дней поступает различный объем данных; в день i вы получаете xi терабайт. За каждый обработанный терабайт ваша фирма получает фиксированную оплату, но все необработанные данные становятся недоступными в конце дня (то есть их обработку нельзя продолжить на следующий день).
Ежедневно обрабатывать все данные не удается из-за возможностей компьютерной системы, способной обрабатывать определенное количество терабайт в день. В системе работает уникальная программа — очень сложная, но не стопроцентно надежная, поэтому максимальный объем обрабатываемых данных убывает с каждым днем, прошедшим с момента последней перезагрузки. В первый день после перезагрузки система может обработать s1 терабайт, во второй день — s2 терабайта и т. д. вплоть до sn; предполагается, что s1 > s2 > s3 > ... > sn > 0. (Конечно, в день iсистема может обработать не более xi терабайт независимо от быстродействия вашей системы.) Чтобы вернуть систему к максимальной производительности, можно перезагрузить ее; однако в любой день, в который система будет перезагружаться, никакие данные вообще не обрабатываются.
Задача. Для заданных объемов данных x1, x2, ..., xn на следующие n дней и профиля системы, описанного серией s1, s2, ..., sn (начиная с только что перезагруженной системы в день 1), выберите дни для проведения перезагрузки, чтобы максимизировать общий объем обрабатываемых данных.
Пример. Допустим, n = 4, а значения xi и si задаются следующей таблицей.
|
День 1 |
День 2 |
День 3 |
День 4 |
|
|
x |
10 |
1 |
7 |
7 |
|
s |
8 |
4 |
2 |
1 |
В оптимальном решении перезагрузка выполняется только в день 2; в этом случае в день 1 обрабатываются 8 терабайт, затем 0 терабайт в день 2, 7 терабайт в день 3 и 4 терабайта в день 4, итого 19. (Обратите внимание: без перезагрузки было бы обработано только 8 + 1 + 2 + 1 = 12 терабайт, а с другими стратегиями перезагрузки также получается менее 19 терабайт.)
(a) Приведите пример, обладающий следующими свойствами:
• Объем поставляемых данных превышает возможности обработки, то есть xi > si для каждого i.
• В оптимальном решении система перезагружается минимум дважды. Кроме примера, приведите оптимальное решение. Предоставлять доказательства его оптимальности не обязательно.
(b) Предложите эффективный алгоритм, который получает значения x1, x2, ..., xn и s1, s2, ..., sn и возвращает общее количество терабайт, обрабатываемых оптимальным решением.
10. Вы пытаетесь провести крупномасштабное моделирование физической системы, вычислительная модель которого должна содержать как можно больше дискретных шагов. В вашей лаборатории установлены два суперкомпьютера (назовем их A и B), способных выполнить эту работу. Тем не менее вы не являетесь привилегированным пользователем ни на одном из этих компьютеров и можете использовать только выделенные вам вычислительные ресурсы.
При этом вы сталкиваетесь с проблемой: в любую минуту задание может работать только на одной из этих машин. Для каждой из ближайших n минут доступен “профиль”, который описывает свободные вычислительные мощности на каждой машине. В минуту i можно провести аi > 0 шагов моделирования, если задание выполняется на машине A, или bi > 0 шагов, если задание выполняется на машине B. У вас также есть возможность передать задание с одной машины на другую, но передача занимает минуту времени, в течение которой задание не обрабатывается.
Итак, для заданной последовательности из n минут план определяется выбором действия (A, B или переход) с тем свойством, что варианты A и B не могут следовать непосредственно друг за другом. Например, если в минуту i задание выполняется на машине A и вы хотите переключиться на машину B, то в минуту i + 1 должно быть выбрано действие перехода и только в минуту i + 2 можно будет выбрать B. Значение плана вычисляется как общее количество шагов моделирования, выполненных за n минут; таким образом, оно представляет собой сумму аi по всем минутам, в течение которых задание выполняется на машине A, вместе с суммой bi по всем минутам, в течение которых задание выполняется на машине B.
Задача. Для заданных значений а1, а2, ..., an и b1, b2, ..., bn найдите план с максимальным значением. (Такая стратегия будет называться оптимальной.) План может начинаться с любой из машин A и B в минуту 1.
Пример. Допустим, n = 4, а значения а1, а2, ..., an и b1, b2, ..., bn задаются следующей таблицей.
|
Минута 1 |
Минута 2 |
Минута 3 |
Минута 4 |
|
|
A |
10 |
1 |
1 |
10 |
|
B |
5 |
1 |
20 |
20 |
В плане с максимальным значением в минуту 1 задание выполняется на машине A, затем в минуту 2 происходит переход, а в минуты 3 и 4 задание выполняется на машине B. Значение этого плана составит 10 + 0 + 20 + 20 = 50.
(a) Покажите, что следующий алгоритм не дает правильного решения этой задачи; для этого приведите пример экземпляра задачи, для которого алгоритм возвращает неправильный ответ.

В своем примере укажите правильный ответ и объясните, какой результат находит приведенный алгоритм.
(b) Предложите эффективный алгоритм, который получает значения а1, а2, ..., аn и b1, b2, ..., bn, и возвращает значение оптимального плана.
11. Вы работаете на компанию, которая производит компьютерное оборудование и рассылает его фирмам-дистрибьюторам по всей стране. Для каждой из следующих п недель установлен запланированный объем поставки si (в килограммах) оборудования, которое пересылается грузовым авиаперевозчиком.
• Грузы каждой недели могут перевозиться одной из двух фирм-перевозчиков, A или B. Компания A взимает фиксированную плату r за килограмм (так что стоимость еженедельной поставки составляет r ∙ si).
• Компания B заключает контракты на фиксированную сумму c независимо от веса. При этом контракты с компанией B должны заключаться сразу на четыре недели подряд.
Назовем графиком выбор авиаперевозчика (A или B) для каждой из n недель — с тем ограничением, что компания B, когда она выбирается, должна выбираться на четыре недели подряд. Стоимость графика вычисляется как общая сумма, выплаченная компаниям A и B в соответствии с приведенным выше описанием. Предложите алгоритм с полиномиальным временем, который получает последовательность объемов поставок s1, s2, ..., sn и возвращает график с минимальной стоимостью.
Пример. Допустим, r = 1, с = 10, а серия поставок имеет вид
11, 9, 9, 12, 12, 12, 12, 9, 9, 11.
В этом случае в оптимальном графике компания A выбирается на первые три недели, затем компания B на четыре следующие недели и снова компания A на три последние недели.
12. Допустим, вы хотите реплицировать файл в группе из n серверов, обозначенных S1, S2, ..., Sn. За размещение копии файла на сервере S. вносится целочисленная оплата сi > 0.
Если пользователь запрашивает файл с сервера Si, а копия файла на этом сервере отсутствует, система по порядку проверяет серверы Si+1, Si+2, Si+3, ..., пока не найдет копию файла — например, на сервере Sj, где j > i. Передача файла с другого сервера требует оплаты в размере j - i. (Обратите внимание: серверы с меньшими индексами Si-1, Si-2, ... в поиск не включаются). Стоимость передачи равна 0, если копия файла доступна на сервере Si. Копия файла обязательно размещается на сервере Sn, так что все операции поиска гарантированно завершатся на Sn.
Требуется разместить копии файлов на серверах так, чтобы сумма оплаты за размещение и передачу файлов была минимальной. Формально конфигурацией называется решение о том, должна ли размещаться копия файла на каждом сервере Si для i = 1, 2, ..., n - 1. (Еще раз напомним, что копия всегда размещается на сервере Si.) Общая стоимость конфигурации вычисляется как сумма всех оплат за размещение на серверах с копией файла и сумма всех оплат за передачу файлов, связанных с n серверами.
Предложите алгоритм с полиномиальным временем для поиска конфигурации с минимальной общей стоимостью.
13. Задача поиска циклов в графах естественным образом встречается в системах электронной торговли. Допустим, фирма выполняет операции с акциями n разных компаний. Для каждой пары i ≠ j поддерживается обменный курс rij, который означает, что одна акция i обменивается на rij акций j. Курс может быть дробным: иначе говоря, rij = 2/3 означает, что вы можете отдать три акции i для получения двух акций j.
Обменный цикл для серии акций i1, i2, ..., ik состоит из последовательного обмена акций компании i1 на акции компании i2, затем акций компании i2 на акции компании i3, и т. д.; в конечном итоге акции ik обмениваются на акции i1. После такой серии обменов фирма получает акции той же компании с которой все начиналось. Циклические операции обычно нежелательны, поскольку, как правило, в результате у вас остается меньше акций, чем было в самом начале. Но время от времени на короткий промежуток времени открывается возможность увеличить количество акций. Цикл, операции по которому приводят к увеличению количества исходных акций, будем называть благоприятным циклом. Такая возможность открывается в точности тогда, когда произведение всех дробей в цикле превышает 1. Фирма анализирует состояние рынка и хочет знать, существуют ли на нем благоприятные циклы.
Предложите алгоритм с полиномиальным временем для поиска благоприятного цикла (если он существует).
14. Большая группа мобильных устройств может образовать естественную сеть, в которой устройства являются узлами, а два устройства x и у соединяются ребром, если они могут напрямую взаимодействовать друг с другом (например, по каналу радиосвязи ближнего действия). Такие сети беспроводных устройств чрезвычайно динамичны: ребра появляются и исчезают при перемещении устройства. Например, ребро (x, у) может исчезнуть, когда x и у отдалятся друг от друга и потеряют возможность взаимодействовать напрямую.
В сети, изменяющейся со временем, естественно возникает задача поиска эффективных способов поддержания путей между заданными узлами. При поддержании такого пути приходится учитывать два противоположных фактора: пути должны быть короткими, но при этом путь не должен часто изменяться при изменении структуры сети. (Другими словами, нам хотелось бы, чтобы один путь продолжал работать даже при добавлении и исчезновении ребер, если это возможно.) Ниже описан возможный способ моделирования этой задачи.
Предположим, имеется множество мобильных узлов V, в какой-то момент времени существует множество Е0 ребер между этими узлами. При перемещении узлов множество ребер преобразуется из Е0 в Е1, затем в Е2, затем в Е3 и т. д., вплоть до множества ребер Еb. Для i = 0, 1, 2, ..., b граф (V, Е) обозначается Gi. Итак, если рассматривать структуру сети на базе узлов V “по кадрам”, она будет представлять собой последовательность графов G0, G1, G2, ..., Gb-1, Gb. Предполагается, что все эти графы G являются связными.
Теперь рассмотрим два конкретных узла s, t ∈ V. Для пути s-t P в одном из графов Gi длина P определяется как количество ребер в P; обозначим ее l(P). Наша цель — построить такую последовательность путей P0, P1, ..., Pb, чтобы для каждого i существовал путь s-t Pi в Gi. Пути должны быть относительно короткими. Кроме того, нежелательно слишком большое количество изменений — точек, в которых изменяется структура пути. Формально определим changes(P0, P1, ..., Pb) как количество индексов i (0 ≤ i ≤ b - 1), для которых Pi ≠ Pi+1.
Возьмем фиксированную константу K > 0. Стоимость последовательности путей P0, P1, ..., Pb определяется по формуле
![]()
(a) Предположим, можно выбрать один путь P, который является путем s-t в каждом из графов G0, G1, ..., Gb. Предложите алгоритм с полиномиальным временем для нахождения кратчайшего из таких путей.
(b) Предложите алгоритм с полиномиальным временем для нахождения последовательности путей Р0, P1, ..., Рb с минимальной стоимостью, где Рi является путем s-t в Gi для i = 0, 1, ..., b.
15. В ясные дни ваши друзья с астрономического факультета собираются и договариваются о том, какие астрономические события они будут наблюдать этой ночью. Об этих событиях известно следующее.
• Всего существуют n событий; для простоты мы будем считать, что они происходят последовательно с интервалом ровно в одну минуту. Таким образом, событиеj происходит в минуту j; если астрономы не наблюдают за ним ровно в минуту j, то они пропустят это событие.
• Небесный свод размечен в одномерной координатной системе (в градусах от некоторой центральной базовой линии); событие j происходит в точке с координатой dj для некоторого целого dj. В минуту 0 телескоп направлен в координату 0.
• Последнее событие n намного важнее других; наблюдать за ним обязательно.
У астрономического факультета имеется большой телескоп, в который можно наблюдать все эти события. Телескоп устроен очень сложно и может поворачиваться только на один градус в минуту. Астрономы не надеются пронаблюдать за всеми n событиями; они хотят всего лишь увидеть как можно больше с учетом ограничений телескопа и требования об обязательном наблюдении последнего события.
Назовем подмножество S событий наблюдаемым, если возможно наблюдать каждое событие j ∈ S в назначенное время j и у телескопа хватает времени (с поворотом максимум на один градус в минуту) на перемещение между последовательными событиями S.
Задача. По координатам каждого из n событий найдите наблюдаемое подмножество максимального размера с учетом требования, что оно должно содержать событие n. Назовем такое решение оптимальным.
Пример. Одномерные координаты событий приведены в следующей таблице.
|
События |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Координаты |
1 |
-4 |
-1 |
4 |
5 |
-4 |
6 |
7 |
-2 |
В этом случае в оптимальном решении наблюдаются события 1, 3, 6 и 9. Обратите внимание: у телескопа хватает времени на перемещение от одного события к другому, хотя он и поворачивается всего на один градус в минуту.
(а) Покажите, что следующий алгоритм не дает правильного решения этой задачи; для этого приведите пример экземпляра задачи, для которого алгоритм возвращает неправильный ответ.
![]()

В своем примере укажите правильный ответ и объясните, какой результат находит приведенный алгоритм.
(b) Предложите эффективный алгоритм, который получает координаты d1, d2, ..., d1, d2, ..., dn событий и возвращает размер оптимального решения.
16. В Итаке (штат Нью-Йорк) много солнечных дней; но в этом году весенний пикник фирмы, в которой работают ваши друзья, пришелся на ненастье. Директор фирмы решает отменить пикник, но для этого нужно оповестить всех участников по телефону. Вот как он решает это сделать.
У каждого работника фирмы, кроме директора, есть начальник. Таким образом, иерархия может быть описана деревом T, корнем которого является директор, а у любого другого узла v имеется родительский узел и, представляющий его начальника. Соответственно, мы будем называть v прямым подчиненным по отношению к и. На рис. 6.30 узел A обозначает директора, узлы B и D — прямых подчиненных A, а узел C — прямого подчиненного B.
Чтобы оповестить всех об отмене пикника, директор сначала поочередно звонит каждому из своих прямых подчиненных. Сразу же после звонка подчиненный должен оповестить каждого из своих прямых подчиненных (тоже поочередно). Процесс продолжается до тех пор, пока не будут оповещены все сотрудники. Обратите внимание: каждый участник процесса звонит только своим прямым подчиненным: например, на рис. 6.30 директор A не будет звонить C.
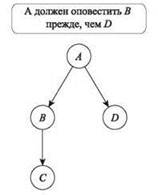
Рис. 6.30. Иерархия с четырьмя участниками. В самой быстрой схеме оповещения A звонит B в первом раунде. Во втором раундеA звонит D, а B звонит C. Если бы A начал со звонка D, то C не узнал бы о новостях до третьего шага
Можно рассматривать процесс распространения информации как разделенный на раунды. В одном раунде каждый работник, уже знающий об отмене, звонит одному из своих прямых подчиненных по телефону. Количество раундов, необходимое для оповещения всех участников, зависит от последовательности, в которой каждый участник звонит своим прямым подчиненным. Например, на рис. 6.30 оповещение будет состоять из двух раундов, если A сначала позвонит B, но займет целых три раунда, если A начнет со звонка D.
Предложите эффективный алгоритм для определения минимального количества раундов, необходимого для оповещения всех участников. Алгоритм должен выводить последовательность телефонных звонков, при которой достигается этот минимум.
17. Ваши друзья занимаются анализом динамики цен на акции технологических фирм. Они определили закономерность, которая была названа возрастающим трендом; формальное описание этой закономерности приводится ниже. Известна последовательность цен на некие акции P[1], P[2], ..., P[n], зафиксированных на момент закрытия биржи для n последовательных дней. Возрастающим трендом в этой серии называется такая подпоследовательность P[i1], P[i2], ..., P[ik] для дней i1 < i2 < ... < ik, у которой:
• i1 = 1;
• P[ij] < P[jj+1] для всех j = 1, 2, ..., k - 1.
Таким образом, возрастающий тренд представляет собой подпоследовательность дней (начинающуюся с первого дня и не обязательно непрерывную), в которой цена строго возрастает.
Требуется найти самый длинный возрастающий тренд для заданной последовательности цен.
Пример. Допустим, n = 7, а последовательность цен выглядит так:
10, 1, 2, 11, 3, 4, 12.
В этом случае самый длинный возрастающий тренд образуется в дни 1, 4 и 7. Обратите внимание: дни 2, 3, 5 и 6 тоже образуют серию возрастающих цен, но так как эта подпоследовательность не начинается с дня 1, она не соответствует определению возрастающего тренда.
(а) Покажите, что следующий алгоритм не всегда возвращает длину самого длинного возрастающего тренда; для этого приведите пример экземпляра задачи, для которого алгоритм возвращает неправильный ответ.

В своем примере приведите длину самого длинного возрастающего тренда и укажите, какой результат находит приведенный алгоритм.
(b) Предложите эффективный алгоритм, который получает последовательность цен P[1], P[2], ..., P[n] и возвращает длину самого длинного возрастающего тренда.
18. Рассмотрим задачу выравнивания последовательностей для алфавита из четырех букв {z1, z2, z3, z4} с заданными стоимостями разрыва и несовпадения. Предположим, каждый из этих параметров является положительным целым числом. Имеются две строки A = a1a2...am и B = b1b2...bn с предложенным выравниванием между ними. Предложите алгоритм O(mn), который решит, является ли выравнивание уникальным выравниванием минимальной стоимости между A и B.
19. Вы консультируете группу специалистов (лучше обойтись без подробностей), занимающихся отслеживанием и анализом электронных сигналов от кораблей в прибрежных водах Атлантики. Они хотят получить быстрый алгоритм для базовой операции, который встречается достаточно часто: “распутывание” суперпозиции двух известных сигналов. А именно, ваши работодатели представляют ситуацию, в которой два корабля снова и снова передают короткую последовательность из 0 и 1; нужно убедиться в том, что полученный сигнал представляет собой результат простого чередования этих двух передач и в него не добавлено ничего лишнего.
Немного уточним формулировку задачи. Для заданной строки х, состоящей из 0 и 1, xk обозначает результат конкатенации к копий строки х. Мы будем называть строку х' повторением х, если она является префиксом хk для некоторого числа k. Таким образом, х' = 10110110110 является повторением х = 101.
Строка s называется чередованием х и у, если ее символы можно разбить на две (необязательно смежные) последовательности s' и s'', так что s' является повторением х, а s'' является повторением у. (При этом каждый символ s принадлежит либо s', либо s''). Например, если х = 101 и у = 00, строка s = 100010101 является чередованием х и у, поскольку символы 1, 2, 5, 7, 8, 9 образуют серию 101101 (повторение х), а оставшиеся символы 3, 4 и 6 образуют серию 000 — повторение у.
В контексте нашего приложения х и у являются повторяющимися последовательностями, полученными от двух кораблей, а s — прослушиваемый сигнал: нужно убедиться в том, что s“разворачивается” в простые повторения х и у. Предложите эффективный алгоритм, который получает строки s, х и у и решает, является ли s чередованием х и у.
20. Семестр близится к завершению, и вам предстоит выполнить курсовые проекты по п учебным курсам. За каждый проект будет выставлена оценка — целое число в диапазоне от 1 до g > 1; более высокие числа означают лучшие оценки. Разумеется, вы стремитесь к максимизации средней оценки по n проектам.
Вы располагаете временем H > n часов для работы над проектами (с перерывами); нужно решить, как распределить это время. Для простоты будем считать, что H — положительное целое число и на каждый проект расходуется целое количество часов. Чтобы определить, как лучше распределить время, вы определяете множество функций {fi: i = 1, 2, n} (конечно, оценки весьма приблизительные) для каждого из n проектов: потратив h ≤ H часов на проект по курсу i, вы получите оценку fi(h). (Функции fi не убывают: если h < h', то fi(h) ≤ fi(h').)
Задача. Для заданный функций {fi} решите, сколько часов следует потратить на каждый проект (только в целых числах), чтобы средняя оценка, вычисленная в соответствии с fi, была как можно больше. Для повышения эффективности время выполнения алгоритма должно быть полиномиальным по n, g и H: ни одна из этих величин не должна входить в экспоненциальную зависимость времени выполнения.
21. Совсем недавно вы помогали своим друзьям, которые занимались обменом акций, а они пришли к вам с новой задачей. Имеются данные по курсу некоторых акций за n дней подряд (в какое-то время в прошлом). Дни пронумерованы i = 1, 2, ..., n; для каждого дня i известна цена акции p(i) за этот день.
Для некоторых (возможно, больших) значений k требуется проанализировать так называемые k-операционные стратегии — множества из m пар за дни (b1, s1), ..., (bm, sm), где 0 ≤ m ≤ k и
![]()
Они рассматриваются как множество из к неперекрывающихся интервалов, во время каждого из которых инвесторы покупают 1000 акций на бирже (в день bi), а затем продают их (в день si). Доход от k-операционной стратегии определяется как прибыль, полученная в результате m операций купли-продажи, а именно
![]()
Инвесторы хотят оценить значение k-операционных стратегий по результатам моделирования своих n-дневных данных котировок. Ваша цель — спроектировать эффективный алгоритм, который определяет для заданной серии цен k-операционную стратегию с максимально возможным доходом. Так как значение k в этих моделях может быть достаточно большим, время выполнения должно быть полиномиальным по n и k (значение к не должно присутствовать в экспоненте).
22. Чтобы оценить, насколько “надежно связаны” два узла в направленном графе, можно рассмотреть не только длину кратчайшего пути между ними, но и количество кратчайших путей.
Как выясняется, эта задача имеет эффективное решение при некоторых ограничениях на стоимости ребер. Допустим, имеется направленный граф G = (V, E) со стоимостями ребер; стоимости могут быть как положительными, так и отрицательными, но каждый цикл в графе имеет строго положительную стоимость. Также даны два узла v, w ∈ V. Предложите эффективный алгоритм для вычисления количества кратчайших путей v-w в G. (Алгоритм не должен выводить все пути; достаточно только одного количества.)
23. Имеется направленный граф G = (V, E) со стоимостями ребер ce для e ∈ E и стоком t (стоимости могут быть отрицательными). Также предполагается наличие конечных значений d(v) для v ∈V. Утверждается, что для каждого узла v ∈ V величина d(v) определяет стоимость пути с минимальной стоимостью от узла v к стоку t.
(a) Предложите алгоритм с линейным временем (время O(m), если граф содержит m ребер), который проверяет правильность этого утверждения.
(b) Предположите, что расстояния верны, а d(v) конечны для всех v ∈ V. Теперь требуется вычислить расстояния до другого стока t'. Предложите алгоритм O(m log n) для вычисления расстояний d'(v) от всех узлов v ∈ V к стоку t'. (Подсказка: будет полезно рассмотреть новую функции стоимости, которая определяется следующим образом: для ребра e = (v, w) пусть c'e = ce- d(v) + d(w). Связаны ли между собой стоимости путей для двух разных с и c'?)
24. Перекраиванием называется практика тщательно продуманного изменения избирательных округов, при котором результат оказывается угодным конкретной политической партии. В ходе разбирательств по недавним судебным искам было показано, что тщательное перекраивание приводит к фактическому (и намеренному) лишению избирательного права больших групп избирателей. Как выясняется, при описании этой темы в новостях “источником зла” называют компьютеры: благодаря мощным программам перекраивание превратилось из занятия группы людей с картами, карандашами и блокнотами в высокотехнологичный процесс. Почему перекраивание стало вычислительной задачей? Базы данных позволяют отследить демографию избирателей до уровня отдельных улиц и домов, а группировка избирателей по округам создает некоторые проблемы чисто алгоритмического плана.
Допустим, имеется множество из n участков P1, P2, ..., Pn, каждый из которых содержит m зарегистрированных избирателей. Требуется разделить эти участки на два округа, каждый из которых состоит из n/2 участков. Для каждого участка доступна информация о том, сколько избирателей поддерживают каждую из двух политических партий. (Для простоты будем считать, что каждый избиратель поддерживает одну из двух партий.) Множество участков будет подвержено перекраиванию, если возможно выполнить разбиение на два округа таким образом, что одна партия будет иметь большинство в обоих округах.
Предложите алгоритм для определения того, подвержено ли заданное множество участков перекраиванию; время выполнения алгоритма должно быть полиномиальным по n и m.
Пример. Допустим, имеется n = 4 участков и доступна следующая информация о зарегистрированных избирателях.
|
Участок |
1 |
2 |
3 |
4 |
|
Количество зарегистрированных сторонников партии A |
55 |
43 |
60 |
47 |
|
Количество зарегистрированных сторонников партии B |
45 |
57 |
40 |
53 |
Это множество участков создает опасность перекраивания: если сгруппировать участки 1 и 4 в один округ, а участки 2 и 3 — в другой, партия A получит большинство в обоих округах (предполагается, что группировку выполняют члены партии A). Этот пример наглядно демонстрирует изначальную несправедливость перекраивания: хотя партия A имеет небольшое преимущество в общем населении (205 к 195), она получает преимущество не в одном, а в обоих округах.
25. Биржевой брокер пытается продать большое количество акций, цена которых неуклонно снижается. Всегда трудно спрогнозировать идеальный момент для продажи акций, но держатели большого количества акций одной компании сталкиваются с дополнительной проблемой: сам факт продажи большого количества акций в один день отрицательно влияет на цену.
Будущие рыночные цены и эффект от продажи большого количества акций очень трудно спрогнозировать, брокерские фирмы используют модели рынка для принятия решений. В этой задаче рассматривается очень простая модель: допустим, нужно продать x акций определенного вида и имеется достаточно точная модель рынка: она предсказывает, что цена акций будет принимать значения p1, p2, ..., pn в ближайшие n дней. Кроме того, имеется функция f(∙), прогнозирующая эффект масштабных продаж: если продать у акций в один день, цена с этого дня стабильно снижается на f(у). Итак, при продаже у1 акций в день 1 цена акций снижается до p1 - f(у1) с суммарным доходом y1 ∙ (p1 - f(у1)). После продажи у1 акций в день 1 можно продать у2 акций в день 2 по цене p2 - f(у1) — f(у2); при этом будет получен дополнительный доход в размере у2 ∙ (p2 - f(у1) - f(у2)). Процесс продолжается все n дней. (Обратите внимание: как и вычислениях для дня 2, уменьшение цены за предыдущие дни включается в цену на все последующие дни).
Разработайте эффективный алгоритм, который получает цены p1, ..., pn и функцию f(∙) (записанную в виде списка значений f(1), f(2), ..., f(x)), и определяет лучший вариант продажи x акций ко дню n. Иначе говоря, найдите такие натуральные числа у1, у2, ..., Уn, что x = у1 + ... + уn и продажа у. акций в день i для i = 1, 2, ..., n максимизирует суммарный доход. Стоимость акций piмонотонно убывает, а f(∙) монотонно возрастает; иначе говоря, продажа большего количества акций приводит к более значительному снижению цены. Время выполнения алгоритма может находиться в полиномиальной зависимости от n (количество дней), x (количество акций) и p1 (пиковая цена акций).
Пример. Допустим, n = 3; цены за три дня были равны 90, 80, 40; f(у) = 1 для у < 40 000 и f(у) = 20 для у > 40 000. Предположим, вы начинаете с x = 100 000 акций. При продаже всех акций в день 1 цена составит 70 за акцию, а общий доход — 7 000 000. Если же продать 40 000 акций в день 1 по цене 89 за акцию, а затем продать остальные 60 000 акций в день 2 по цене 59 за акцию, общий доход составит 7 100 000.
26. Вы руководите компанией, которая продает некий крупный товар (допустим, грузовики). Аналитики предоставляют вам прогнозы с предполагаемым объемом продаж за следующие nмесяцев. Обозначим d предполагаемый объем продаж в месяце i. Будем считать, что все продажи происходят в начале месяца, а непроданные грузовики хранятся на складе до начала следующего месяца. На складе помещается максимум S грузовиков, а затраты на хранение одного грузовика в течение месяца равны C. Чтобы получить партию грузовиков с завода, вы размещаете заказ. За каждое размещение заказа (независимо от количества заказанных грузовиков) взимается фиксированная плата K. Изначально на складах нет ни одного грузовика. Требуется разработать алгоритм, который решает, как разместить заказы для выполнения всех требований {di} с минимальными издержками. Вкратце:
• расходы складываются из двух составляющих: 1) хранение — за каждый грузовик на складе, который не продан в этом месяце, приходится платить C; 2) размещение заказа — за каждый заказ приходится платить K;
• в каждом месяце необходимо иметь достаточно грузовиков, чтобы удовлетворить спрос di, но количество оставшихся после этого грузовиков не должно превысить емкость склада S.
Предложите алгоритм, решающий эту задачу за время, полиномиальное по n и S.
27. Владелец бензоколонки столкнулся со следующей проблемой: имеется большой подземный бак, в котором хранится бензин; емкость бака составляет L галлонов. Заказы обходятся дорого, поэтому они оформляются относительно редко. Для каждого заказа владелец должен заплатить фиксированную цену P (кроме стоимости заказанного бензина). Однако хранение галлона в течение дня требует затрат с, поэтому слишком большие запасы увеличивают расходы на хранение. Владелец бензоколонки собирается закрыть ее на неделю зимой. К моменту закрытия бак должен быть пустым. К счастью, на основании многолетнего опыта он может точно предсказать, сколько бензина будет расходоваться ежедневно до заданного момента. Допустим, что до закрытия осталось n дней и в день i (i = 1, ..., n) будет расходоваться gi галлонов. Предполагается, что в конце дня 0 бак пуст. Предложите алгоритм, который решает, в какие дни следует размещать заказы и сколько бензина нужно заказывать для минимизации общих затрат.
28. Вспомните задачу планирования из раздела 4.2, в которой мы стремились к минимизации максимальной задержки. Существуют n заданий, каждое задание имеет предельное время di и необходимое время обработки ti; все задания доступны для планирования, начиная с времени s. Чтобы задание i было выполнено, ему необходимо выделить период времени от si ≥ s до fi = si + ti, причем разным заданиям должны назначаться неперекрывающиеся интервалы. Такое распределение времени называется расписанием.
В этой задаче рассматривается аналогичная ситуация, но оптимизируется другая цель. А именно, мы рассмотрим случай, при котором каждое задание должно быть либо выполнено к предельному времени, либо не выполнено вообще. Подмножество J называется планируемым, если для заданий в J существует расписание, при котором каждое задание будет завершено к предельному времени. Требуется выбрать планируемое подмножество максимального возможного размера и найти для этого подмножества расписание, позволяющее завершить каждое задание к предельному времени.
• (a) Докажите, что существует оптимальное решение J (то есть планируемое множество максимального размера), в котором задания J планируются по возрастанию предельного времени.
• (b) Предположим, все значения предельного времени di и необходимого времени ti являются целыми числами. Предложите алгоритм для поиска оптимального решения. Алгоритм должен выполняться за время, полиномиальное по количеству заданий n и максимальному предельному времени D = maxidi.
29. Граф G = (V, E) состоит из n узлов, каждая пара узлов соединена ребром. Каждому ребру (i, j) присвоен положительный вес wij; предполагается, что веса удовлетворяют неравенству треугольникаwik ≤ wij + wjk. Для подмножества V' ⊆ V запись G[V] обозначает подграф (с весами ребер), построенный для узлов из V'.
Дано множество X ⊆ V из k терминальных узлов, которые должны быть соединены ребрами. Деревом Штейнера для X называется такое множество Z, что X ⊆ Z ⊆ V в сочетании с остовным поддеревом T подграфа G[Z]. Весом дерева Штейнера называется вес дерева T.
Покажите, что существует f(∙) и полиномиальная функция p(∙), для которых задача нахождения дерева Штейнера с минимальным весом для X может быть решена за время O(f(k)∙p(n)).
Примечания и дополнительная литература
Первопроходцем в области систематического изучения динамического программирования был Ричард Беллман (Bellman, 1957); алгоритм сегментированной задачи наименьших квадратов, приведенный в этой главе, основан на одной из ранних работ Беллмана (Bellman, 1961). С тех пор динамическое программирование поднялось до уровня метода, широко используемого в компьютерной науке, исследовании операций, теории управления и ряде других областей. Значительная часть последних разработок по теме относится к стохастическому динамическому программированию: если в нашей формулировке задачи неявно предполагалось, что все входные данные известны с самого начала, многие задачи в области планирования, производства и складского учета и в других областях включают неопределенность, а алгоритмы динамического программирования для этих задач формулируют эту неопределенность по вероятностной формуле. Введение в стохастическое динамическое программирование приведено в книге Росса (Ross, 1983).
В области комбинаторной оптимизации изучались многие расширения и вариации на тему задачи о рюкзаке. Как упоминалось в этой главе, псевдополиномиальная граница, встречающаяся в области динамического программирования, может стать неприемлемой при большом размере входных данных; в таких случаях динамическое программирование часто объединяется с другими эвристиками для практического решения больших экземпляров задачи о рюкзаке. Книга Мартелло и Тота (Martello, Toth, 1990) посвящена вычислительным методам решения разных вариантов задачи о рюкзаке.
Динамическое программирование заняло место среди базовых методов вычислительной биологии в начале 1970-х годов в результате интенсивного изучения задачи сравнения последовательностей. Санкофф (Sankoff, 2000) приводит интересные исторические данные о ранних работах этого периода. В книгах Уотермена (Waterman, 1995) и Гасфилда (Gusfield, 1997) приводится подробное описание алгоритмов выравнивания последовательностей (а также многих сопутствующих алгоритмов в вычислительной биологии); Мэтьюз и Цукер (Mathews, Zukor, 2004) обсуждают будущее методов решения задачи предсказания вторичной структуры РНК. Алгоритм выравнивания последовательностей, эффективных по затратам памяти, был предложен Хиршбергом (Hirschberg, 1975).
Алгоритм для задачи нахождения кратчайшего пути, описанный в этой главе, основан на исходной работе Беллмана (Bellman, 1958) и Форда (Ford, 1956). Этот базовый метод поиска кратчайших путей был дополнен множеством оптимизаций, обусловленных как теоретическими, так и экспериментальными соображениями; на сайте Эндрю Голдберга приведена новейшая версия кода, написанного им для решения этой задачи (а также ряда других) по материалам работы Черкасски, Голдберга и Радзика (Cherkassky, Goldberg, Radzik, 1994). Практическое применение методов нахождения кратчайших путей для маршрутизации в Интернете, а также достоинства и недостатки разных алгоритмов сетевых приложений описаны в книгах Бертсекаса и Галлагера (Bertekas, Gallager, 1992), Кешава (Keshav, 1997) и Стюарта (Stewart, 1998).
Примечания к упражнениям
Упражнение 5 было создано по мотивам обсуждения с Лилиан Ли; упражнение 6 основано на результатах Дональда Кнута; упражнение 25 основано на результатах Димитриса Бертсимаса и Эндрю Ло; упражнение 29 основано на результатах С. Дрейфуса и Р. Вагнера.
1 В этом анализе во времени выполнения доминирует фактор O(n3), необходимый для вычисления всех значений ei,j. Но на самом деле все эти значения можно вычислить за время O(n2), что сокращает время выполнения всего алгоритма до O(n2). Идея, подробности которой остаются читателю для самостоятельной работы, заключается в том, чтобы сначала вычислить ei,j для всех пар (ij), для которых j - i = 1, затем для всех пар с j - i = 2, затем для j - i = 3 и т. д. Таким образом, добравшись до конкретного значения ei,j, мы можем использовать ингредиенты вычисления ei,j - 1 для определения ei,j за постоянное время.
2 Аденин, гуанин, цитозин и тимин — четыре основные структурные единицы ДНК.
3 Заметьте, что символ T из алфавита ДНК заменяется символом U, но для нас это сейчас несущественно.