Сегментация изображений - Нахождение потока в сети

Центральное место в компьютерной обработке изображений занимает сегментация изображения. Например, на изображении могут быть представлены три человека на сложном фоне. Естественная, но непростая задача заключается в идентификации каждого из трех людей как отдельного объекта.

Задача

Одна из основных задач этого направления — отделение переднего плана от фона: каждый пиксел изображения помечается как принадлежащий либо к переднему плану, либо к фону. Как выясняется, чрезвычайно естественная модель такого разбиения приводит к задаче, эффективно решаемой посредством вычисления минимального разреза.

Обозначим V множество пикселов анализируемого изображения. Некоторые пары пикселов объявляются соседями; пусть E — множество всех пар соседних пикселов. Таким образом будет получен ненаправленный граф G = (V, E). Здесь мы намеренно не даем четкого определения того, что подразумевается под “пикселом” или “соседским” отношением. Для любого графа Gбудет получено эффективное решение задачи, поэтому мы можем определять эти концепции так, как считаем нужным. Конечно, пикселы естественно представлять, как точки, образующие сетку; при этом соседями считаются пикселы, занимающие смежные позиции в этой сетке, как показано на рис. 7.18, а.

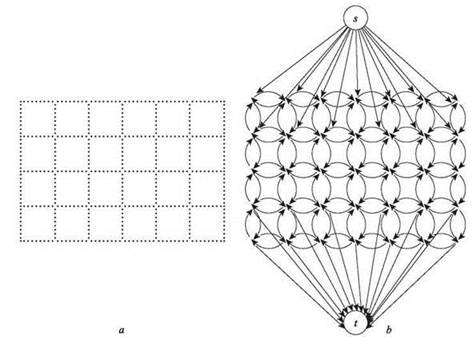
Рис. 7.18. а — матрица пикселов; b — схема соответствующего потокового графа; на схеме изображены не все ребра от источника к стоку

Для каждого пиксела i имеется степень правдоподобия а_i того, что он принадлежит переднему плану, и степень правдоподобия b_i того, что он принадлежит фону. Условно будем считать, что величины правдоподобия представляют собой произвольные неотрицательные числа, содержащиеся в постановке задачи, и они указывают, насколько желательно, чтобы пиксел i считался относящимся к переднему плану или фону. В остальном не так важно, какие физические свойства изображения оценивают эти характеристики и как они вычисляются.

Каждой отдельный пиксел i было бы разумно отнести к переднему плану, если а_i > b_i, или к фону в противном случае. Однако решение относительно i зависит от решений, принимаемых относительно соседей i. Например, если многие соседи i помечены как относящиеся к фону, то у нас появляется больше оснований отнести к фону i; это приводит к “сглаживанию” границ между фоном и передним планом, и снижению длины границы. Для каждой пары соседних пикселов (i, j) вводится штраф за разделениеp_ij ≥ 0, применяемый в том случае, если один пиксел пары относится к переднему плану, а другой к фону.

А теперь мы можем точно определить задачу сегментации в контексте параметров правдоподобия и штрафа за разделение. Требуется найти разбиение множества пикселов на подмножества A и B (передний план и фон соответственно), максимизирующее

Таким образом, высокие значения правдоподобия награждаются, а соседние пары (i, j), в которых один пиксел принадлежит A, а другой принадлежит B, штрафуются. Задача заключается в вычислении оптимальной разметки — разбиения (A, B), максимизирующей q(A, B).

Разработка и анализ алгоритма

Нетрудно заметить сходство между задачей о минимальном разрезе и задачей нахождения оптимальной разметки. Тем не менее между этими задачами также существует ряд важных различий. Во-первых, целевая функция максимизируется, а не минимизируется. Во-вторых, в задаче разметки нет источника и стока; кроме того, нам приходится иметь дело со значениями а_i и b_i узлов. В-третьих, граф G является ненаправленным, тогда как в задаче о минимальном разрезе используется направленный граф. Все эти проблемы кратко рассмотрены ниже.

Первая проблема — тот факт, что задача сегментации направлена на максимизацию — решается следующим наблюдением. Пусть Сумма не отличается от суммы что позволяет записать

Таким образом, мы видим, что задача максимизации q(A, B) эквивалентна задаче максимизации величины

Что касается отсутствия источника и стока, мы поступим так же, как в других предшествующих построениях: создадим новый “суперисточник” s, представляющий передний план, и новый “суперсток”, представляющий фон. Заодно это позволит разобраться со значениями а_i и b_i, находящимися в узлах (тогда как минимальные разрезы ограничиваются числами, связанными с ребрами). А именно, каждый из узлов s и t соединяется с каждым пикселом, а а_i и b_i используются для определения соответствующих пропускных способностей ребер между пикселом i и источником и стоком соответственно.

Наконец, чтобы разобраться с направленностью ребер, мы смоделируем каждую из соседних пар (i, j) двумя направленными ребрами (i, j) и (j, i), как было сделано в ненаправленной задаче о непересекающихся путях. Этот прием очень хорошо работает в данном случае, так как в любом разрезе s-t не более одного из двух противоположно направленных ребер может переходить со стороны s на сторону t разреза (потому что другое ребро в этом случае должно переходить со стороны t на сторону s).

Конкретнее, мы определяем следующую потоковую сеть G' = (V', E'), изображенную на рис. 7.18, b. Множество узлов V' состоит из множества пикселов V с двумя дополнительными узлами s и t. Для каждой соседней пары пикселов i и j добавляются направленные ребра (i, j) и (j, i), каждое из которых обладает пропускной способностью p_ij. Для каждого пиксела i добавляются ребро (s, i) с пропускной способностью а_i, и ребро (i, t) с пропускной способностью b_i.

Теперь разрез s-t (A, B) соответствует разбиению пикселов на множества A и B. Рассмотрим, как пропускная способность разреза c(A, B) связана с величиной q'(A, B), которую мы пытаемся минимизировать Ребра, пересекающие разрез (A, B), делятся на три естественные категории.

♦ Ребра (s, j), для которых j ∈ B; такое ребро вносит вклад а_j в пропускную способность разреза.

♦ Ребра (i, t), для которых i ∈ A; такое ребро вносит вклад b_i в пропускную способность разреза.

♦ Ребра (i, j), для которых i ∈ A и j ∈ B; такое ребро вносит вклад p_ij в пропускную способность разреза.

На рис. 7.19 на примере с четырьмя пикселами показано, как выглядит каждый из трех видов ребер относительно разреза.

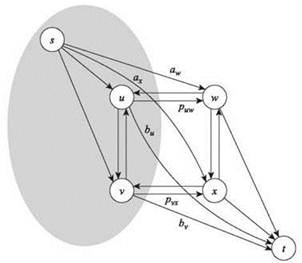
Рис. 7.19. Разрез s-t на графе, построенном для четырех пикселов. Обратите внимание на то, как в разрезе отражены три типа слагаемых в выражении q'(A, B)

Суммируя вклады этих трех типов ребер, получаем

Итак, все идеально складывается. Потоковая сеть устроена так, что пропускная способность разреза (A, B) в точности соответствует величине q'(A, B): три типа ребер, пересекающих разрез (A, B), которые мы определили (ребра от источника, ребра к стоку и ребра, не связанные ни с источником, ни со стоком), соответствуют трем типам слагаемых в выражении q'(A, B).

Следовательно, если мы хотим минимизировать q'(A, B) (что, как было показано ранее, эквивалентно максимизации q(A, B)), достаточно найти разрез с минимальной пропускной способностью — а мы уже знаем, как эффективно решить эту задачу.

Таким образом, решение задачи о минимальном разрезе дает оптимальный алгоритм для решения задачи об отделении фона от переднего плана.

(7.55) Решение задачи сегментации может быть получено при помощи алгоритма нахождения минимального разреза в графе G', построенного ранее. Для минимального разреза (A', B') разбиение (A, B), полученное удалением s* и t*, максимизирует метрику сегментации q(A, B).