Сведение с применением регуляторов: задача выполнимости - NP-полнота и вычислительная неразрешимость

Сейчас мы займемся более абстрактными задачами, которые формулируются в булевой записи. Эти задачи применяются для моделирования широкого спектра задач, в которых требуется присваивать значения условных переменных для выполнения заданного набора ограничений: например, подобные формальные конструкции часто встречаются в области искусственного интеллекта. После знакомства с этими задачами мы свяжем их посредством сведения с задачами графов и множеств, рассматривавшимися ранее.

Задачи SAT и 3-SAT

Допустим, имеется множество X из n булевых переменных x₁, ..., x_n; каждая переменная может принимать значение 0 или 1 (эквиваленты false и true). Литералом по X называется одна из переменных х. или ее отрицание . Наконец, условием называется обычная дизъюнкция литералов

t₁ V t₂ V ... V t_i.

(Еще раз: все ). Мы говорим, что условие имеет длину l, если оно содержит l литералов.

А теперь дадим формальное определение присваиванию значений, удовлетворяющих набору условий. Логическим присваиванием для X называется присваивание значения 0 или 1 каждому х_i; другими словами, это функция v: Х → {0,1}. Присваивание v неявно задает значение истинности, противоположное х_i. Присваивание выполняет условие C, если после него C дает результат 1 по условиям булевой логики; это эквивалентно требованию о том, чтобы по крайней мере один из литералов в C имел значение 1. Присваивание выполняет совокупность условий C₁, ..., C_k, если в результате его все C_i дают результат 1; иначе говоря, если в результате его конъюнкция

C₁ Λ C₂ Λ ... Λ C_k

дает результат 1. В этом случае v называется выполняющим присваиванием в отношении C₁, ..., C_k, а набор условий C₁, ..., C_k называется выполнимым.

Рассмотрим простой пример. Допустим, имеются три условия:

Логическое присваивание v, которое задает всем трем переменным значение 1, не является выполняющим, потому что с ним не выполняется второе из перечисленных условий; с другой стороны, присваивание v', которое задает всем переменным значение 0, является выполняющим.

Теперь можно привести формулировку задачи выполнимости, также обозначаемой SAT:

Для заданного множества условий C₁, ..., C_k по множеству переменных X = {х₁, ..., x_n} существует ли выполняющее логическое присваивание?

Существует частный случай SAT, обладающий эквивалентной сложностью, но при этом более понятный; в нем все условия содержат ровно три литерала (соответствующих разным переменным). Назовем эту задачу задачей 3-выполнимости, или 3-SAT:

Для заданного множества условий C₁, ..., C_k, каждое из которых имеет длину 3, по множеству переменных X = {x₁, ..., х_n}, существует ли выполняющее логическое присваивание?

Задачи выполнимости и 3-выполнимости являются фундаментальными задачами комбинаторного поиска; они содержат основные составляющие сложной вычислительной задаче и в предельно упрощенном виде. Требуется принять п независимых решений (присваивания всем х_i) так, чтобы выполнить набор ограничений. Существуют разные способы выполнения каждого ограничения по отдельности, но решения придется скомбинировать так, чтобы все ограничения выполнялись одновременно.

Сведение задачи 3-SAT к задаче о независимом множестве

А теперь свяжем вычислительную сложность, воплощенную в задачах SAT и 3-SAT, с другой (на первый взгляд) сложностью, представленной поиском независимых множеств и вершинных покрытий в графах, а именно: мы покажем, что 3-SAT ≤_р Независимое множество. Основная трудность в подобных доказательствах очевидна: в задаче 3-SAT речь идет о присваивании значений булевым переменным с учетом ограничений, тогда как задача о независимом множестве направлена на выбор вершин в графе. Чтобы решить экземпляр задачи 3-SAT с использованием “черного ящика” для задачи о независимом множестве, необходимо как-то закодировать все эти булевы ограничения в узлах и ребрах графа, чтобы критерий выполнимости соответствовал существованию большого независимого множества.

Этот прием демонстрирует общий принцип проектирования сложных сведений Y≤_рX: построение “регуляторов” из компонентов в задаче X для представления того, что происходит в задаче Y.

(8.8) 3-SAT ≤_р Независимое множество.

Доказательство. Имеется “черный ящик” для задачи о независимом множестве; мы хотим решить экземпляр задачи 3-SAT, состоящий из переменных X = {х₁, ..., х_n} и условий C₁, ..., C_k.

Чтобы правильно взглянуть на проблему сведения, следует понять, что существуют две концептуально различающиеся точки зрения на экземпляр 3-SAT.

♦ Первый способ представления экземпляра 3-SAT был предложен ранее: для каждой из n переменных принимается независимое решение 0/1, а успех достигается при достижении одного из трех способов выполнения каждого условия.

♦ Тот же экземпляр 3-SAT можно представить иначе: нужно выбрать один литерал из каждого условия, а затем найти логическое присваивание, в результате которого все эти литералы дают результат 1 с выполнением всех условий. Итак, успех достигается в том случае, если вы сможете выбрать литерал из каждого условия так, чтобы никакие два выбранных литерала не “конфликтовали”; мы говорим, что конфликт двух литералов возникает тогда, когда один равен переменной х_i, а другой ее отрицанию . Если удастся избежать конфликтов, мы сможем найти логическое присваивание, в результате которого выбранные литералы из каждого условия дают результат 1.

Следующее сведение базируется на втором представлении экземпляра 3-SAT; мы закодируем его с использованием независимых множеств в графе. Сначала построим граф G = (V,E), состоящий из 3k узлов, сгруппированных в k треугольников, как показано на рис. 8.3. Таким образом, для i = 1, 2, ..., k строятся три вершины v_i1, v_i2, v_i3, соединенные друг с другом ребрами. Каждой вершине присваивается метка; v_ij помечается j-м литералом из условия C_i экземпляра 3-SAT.

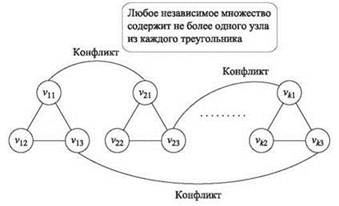
Рис. 8.3. Сведение задачи 3-SAT к задаче о независимом множестве

Прежде чем продолжать, рассмотрим, как выглядят независимые множества с размером k на этом графе: так как две вершины не могут быть выбраны из одного треугольника, они состоят из всех способов выбора одной вершины из каждого треугольника. Так реализуется наша цель по выбору литерала в каждом условии, который дает результат 1; но пока мы не сделали ничего, чтобы предотвратить конфликт между двумя литералами.

Конфликты будут кодироваться добавлением новых ребер в граф: каждую пару вершин, метки которых соответствуют конфликтующим литералам, мы соединяем ребром. Приведет ли это к уничтожению всех независимых множеств размера k или такое множество существует? Это зависит от того, можно ли выбрать один узел из каждого треугольника, чтобы при этом не были выбраны конфликтующие пары узлов. Но ведь именно то, что требуется в экземпляре 3-SAT!

Утверждается, что исходный экземпляр задачи 3-SAT выполним в том и только в том случае, если построенный граф G имеет независимое множество с размером не менее k. Во-первых, если экземпляр 3-SAT выполним, то каждый треугольник в графе содержит как минимум один узел, метка которого дает результат 1. Пусть S — множество, состоящее из одного такого узла в каждом треугольнике. Множество S является независимым; если бы между двумя узлами u, v ∈ S существовало ребро, то метки u и v должны были бы конфликтовать; но это невозможно, так как обе они дают результат 1.

И наоборот, предположим, что граф G содержит независимое множество S с размером не менее k. Тогда прежде всего размер Sравен точно k, и оно должно содержать один узел из каждого треугольника. Далее утверждается, что существует логическое присваивание v для переменных в экземпляре 3-SAT, обладающее тем свойством, что метки всех узлов S дают результат 1. Как же построить такое присваивание v? Для каждой переменной х_i, если ни х_i, ни не используется как метка узла в S, мы присваиваем v(x_i) = 1. В противном случае либо х_i, либо является меткой узла в S; потому что если бы один узел в S был помечен х_i, а другой , то эти два узла были бы соединены ребром, что противоречило бы нашему предположению о том, что S является независимым множеством. Если x_i является меткой узла в S, мы присваиваем v(x_i) = 1; в противном случае выполняется присваивание v(x_i) = 0. При таком построении v все метки узлов в Sдают результат 1.

Так как G содержит независимое множество с размером не менее k в том, и только в том случае, если исходный экземпляр 3-SAT был выполнимым, сведение завершено. ■

Транзитивность сведения

Мы рассмотрели несколько разных сложных задач, относящихся к разным классам, и выяснили, что они тесно связаны друг с другом. Мы можем вычислить несколько дополнительных отношений, используя факт транзитивности ≤_P.

(8.9) Если Z≤_PY и Y≤_PX, то Z≤_PX.

Доказательство. Располагая “черным ящиком” для решения X, мы покажем, как решить экземпляр задачи Z; по сути, мы просто выполняем композицию двух алгоритмов, подразумеваемых Z≤_PY и Y≤_PX. Алгоритм для Z выполняется с использованием “черного ящика” для Y; но каждое обращение к “черному ящику” для Y моделируется полиномиальным количеством шагов, использующих алгоритм, решающий экземпляры Y с использованием “черного ящика” для X. ■ Свойство транзитивности весьма полезно. Например, так как мы доказали, что 3-SAT ≤_PНезависимое множество ≤_P Вершинное покрытие ≤_P Покрытие множества, можно сделать вывод, что 3-SAT ≤_P Покрытие множества.