NР-полные задачи - NP-полнота и вычислительная неразрешимость

Не достигнув прогресса в разрешении вопроса P = NP, ученые обратились к сопутствующему, но более доступному вопросу: какие задачи в NP обладают наибольшей сложностью? Сведение к полиномиальному времени позволяет нам рассмотреть этот вопрос и получить представление о структуре NP.

Возможно, самый естественный способ определения “наиболее сложной” задачи X основан на следующих двух свойствах: (i) X ∈ NP и (ii) для всех Y ∈ NP Y≤_PX. Другими словами, мы требуем, чтобы каждая задача в NP сводилась к X. Такая задача X будет называться NP-полной задачей.

Следующий факт подкрепляет нашу трактовку термина “наиболее сложная”.

(8.12) Допустим, X является NP-полной задачей. Тогда X решается за полиномиальное время в том, и только в том случае, если P = NP.

Доказательство. Очевидно, если P = NP, то задача X решается за полиномиальное время, так как она принадлежит NP. И наоборот, предположим, что X решается за полиномиальное время. Если Y — любая другая задача в NP, то Y≤_PX, а следовательно, из (8.1) задача Y может быть решена за полиномиальное время. Отсюда NP ⊆ P; в сочетании с (8.10) приходим к искомому заключению. ■

Из (8.12) вытекает одно важное следствие: если в NP существует любая задача, которая не решается за полиномиальное время, то никакая NP-полная задача не может быть решена за полиномиальное время.

Выполнимость булевой схемы: первая NР-полная задача

Наше определение NP-полноты имеет очень полезные свойства. Но прежде чем погружаться в увлекательные размышления по этому поводу, стоит остановиться и обратить внимание на один факт: сам факт существования NP-полных задач не так уж очевиден. Почему не могут существовать две несовместимые задачи X' и X", для которых не существует X ∈ NP с тем свойством, что X'≤_PX и X"≤_PX? Почему в NP не может существовать бесконечная последовательность задач X₁, X₂, X₃, ..., каждая из которых строго сложнее предыдущей? Чтобы доказать NP-полноту задачи, необходимо показать, как она может использоваться для кодирования любой задачи из NP. Эта проблема намного сложнее тех, с которыми мы сталкивались в разделах 8.1 и 8.2, когда искали способы кодирования конкретных задач в контексте других.

В 1971 году Кук и Левин независимо показали, как это делается для очень естественных задач в NP. Возможно, самым естественным выбором для первой NP-полной задачи была задача выполнимости булевой схемы(circuit satisfiability), описанная ниже.

Чтобы дать определение задачи, необходимо четко сформулировать, что имеется в виду под “булевой схемой”. Рассмотрим стандартные булевы операторы, которые используются при определении задачи выполнимости: Λ (И), V (ИЛИ) и ¬ (НЕ). Наше определение строится по образцу физической схемы, собранной из логических элементов, реализующих эти операторы. Затем булева схема K определяется как помеченный, направленный ациклический граф наподобие изображенного на рис. 8.4.

Рис. 8.4. Схема с тремя входами, двумя дополнительным источниками, которым присвоены логические значения, и одним выходом

♦ Источники в K (узлы, не имеющие входящих ребер) помечаются одной из констант — 0 или 1 либо именем конкретной переменной. Узлы последнего типа в дальнейшем называются входамисхемы.

♦ Все остальные узлы помечаются одним из булевых операторов Λ, V или ¬; узлы с меткой Λ или V имеют два входящих ребра, а узлы с меткой ¬ — одно входящее ребро.

♦ Также существует один узел, который не имеет выходящих ребер и представляет выход — результат, вычисляемый схемой.

Схема вычисляет функцию своих входов следующим естественным способом. Ребра представляются как “провода”, передающие сигнал 0/1 от узла, из которого они выходят. Любой узел v, кроме источников, получает значения из входящих ребер (или ребра) и применяет к нему оператор, которым он помечен. Результат операции Λ, V или ¬ передается по ребрам (или ребру), выходящим из v. Итоговое значение, производимое схемой, вычисляется в выходном узле.

Для примера рассмотрим схему на рис. 8.4. Двум левым источникам присвоены значения 1 и 0, а следующие три источника соответствуют входам. Если подать на входы значения 1, 0, 1 (слева направо), то в логических элементах второй строки будут получены значения 0, 1, 1, в логических элементах третьей строки — значения 1, 1, и на выходе — значение 1.

Задача выполнимости булевой схемы формулируется следующим образом. Для заданной схемы нужно решить, существует ли распределение значений по входам, для которого на выходе будет получено значение 1. (Если оно существует, схема называется выполнимой, а выполнимым распределением называется распределение, приводящее к значению 1 на выходе). Как только что было показано, наш пример на рис. 8.4 является выполнимым (со значениями 1, 0, 1 на входах). Теорему Кука и Левина можно рассматривать как эквивалентную следующему утверждению.

(8.13) Задача выполнимости булевой схемы является NP-полной.

Как упоминалось выше, чтобы доказать (8.13), следует рассмотреть произвольную задачу X в NP и показать, что X≤_р Выполнимость булевой схемы. Мы не будем описывать доказательство (8.13) во всех подробностях, но понять основную идею, заложенную в его основу, не так уж трудно. Мы используем тот факт, что любой алгоритм, который получает фиксированное количество n битов на входе и выдает ответ “да/нет”, может быть представлен схемой только что определенного типа: такая схема эквивалентна алгоритму в том смысле, что ее результат равен 1 точно для тех входных значений, для которых алгоритм выдает ответ “да”. Более того, если алгоритм выполняется за серию шагов, полиномиальных по n, то схема имеет полиномиальный размер. Этот переход от алгоритма к схеме является частью доказательства (8.13), в которое мы углубляться не будем, хотя оно вполне естественно с учетом того факта, что реализация алгоритмов на физических компьютерах может быть сведена к операциям с используемым множеством логических элементов Λ, V и ¬. (Обратите внимание на важность изменения количества входных битов, в котором отражается основное различие между алгоритмами и схемами: алгоритм обычно без труда справляется с разными вариантами ввода с разной длиной, а в структуре схемы размер входных данных жестко фиксируется.)

Как использовать это отношение между алгоритмами и схемами? Мы пытаемся показать, что X≤_р Выполнимость булевой схемы, — то есть для заданных входных данных s решить, выполняется ли s ∈ X, с использованием “черного ящика” для решения экземпляров задачи выполнимости булевой схемы. Сейчас мы знаем о задаче X лишь то, что у нее имеется эффективный сертифицирующий алгоритм B(∙,∙). Итак, чтобы проверить s ∈ X для конкретных входных данных s длины n, необходимо ответить на следующий вопрос: существует ли t длины p(n), для которого B(s, t) = да?

Мы ответим на этот вопрос при помощи “черного ящика” для задачи выполнимости булевой схемы. Так как нас интересует только ответ для конкретных входных данных s, B(∙,∙) будет рассматриваться как алгоритм для n + p(n) битов (входные данные s и сертификат t), который мы преобразуем в схему K полиномиального размера с n + p(n) источниками. Первые nисточников жестко кодируются значениями битов s, а остальные p(n) источников помечаются переменными, представляющими биты t; последние источники станут входами для K.

Остается заметить, что s ∈ X в том, и только в том случае, если существует такой способ назначить входные биты K, чтобы схема выдавала на выходе 1, — иначе говоря, в том, и только в том случае, если схема K выполнима. Тем самым устанавливается X≤_р Выполнимость булевой схемы и завершается доказательство (8.13). ■

Пример

Чтобы лучше понять суть того, что происходит в доказательстве (8.13), мы рассмотрим простой и конкретный пример. Допустим, имеется следующая задача.

Содержит ли заданный граф G независимое множество из двух узлов?

Обратите внимание: эта задача принадлежит к категории NP. Посмотрим, как решить экземпляр этой задачи построением эквивалентного экземпляра задачи выполнимости булевой схемы.

Следуя структуре приведенного выше доказательства, мы сначала рассмотрим эффективный сертифицирующий алгоритм для этой задачи. Входные данные s представляют граф из n узлов, который будет задаваться битами: для каждой пары узлов будет присутствовать бит, указывающий, соединены ли эти два узла ребром. Сертификат t может задаваться n битами: для каждого узла включается бит, указывающий, принадлежит ли этот узел предлагаемому независимому множеству. Эффективный сертифицирующий алгоритм должен проверить два факта: что по крайней мере два бита в t равны 1 и что никакие два бита в t не равны 1, если они представляют два конца ребра (что определяется соответствующим битом в s).

Теперь для конкретной длины n, соответствующей интересующим нас входным данным s, строится эквивалентная схема K. Предположим, к примеру, что мы хотим получить ответ на задачу для графа G с тремя узлами u, v, w, в котором узел v соединен с u и w. Это означает, что мы имеем дело с вводом длины n = 3. На рис. 8.5 изображена схема, эквивалентная эффективному сертифицирующему алгоритму для нашей задачи с произвольным графом из трех узлов. (Фактически правая часть схемы проверяет, что были выбраны как минимум два узла, а левая — что не были выбраны оба конца любого ребра). Ребра G кодируются константами в первых трех источниках, а остальные три источника (представляющие узлы, включаемые в независимое множество) остаются переменными. Заметим, что выполнимость этого экземпляра задачи выполнимости схемы проверяется передачей 1, 0, 1 на вход. Это соответствует выбору узлов u и w, которые действительно образуют независимое множество из двух узлов в трехузловом графе G.

Доказательство NР-полноты других задач

Утверждение (8.13) открывает путь к более полному пониманию сложных задач в NP: получив первую NP-полную задачу, мы можем обнаружить много больше таких задач при помощи простого наблюдения.

(8.14) Если Y — NP-полная задача, а X — задача в NP, обладающая свойством Y≤_PX, то задача X является NP-полной.

Доказательство. Так как X ∈ NP, необходимо проверить только свойство (ii) определения. Пусть Z — любая задача в NP. Имеем Z≤_PY вследствие NP-полноты Y и Y≤_PX по определению. Из (8.9) следует, что Z≤_PX. ■

Итак, хотя доказательство (8.13) потребовало тяжелой работы по рассмотрению всех возможных задач в NP, доказательство NP-полноты других задач потребовало только сведения от одной, заведомо NP-полной задачи, — благодаря (8.14).

Ранее мы рассмотрели примеры сведения для некоторых базовых вычислительно сложных задач. Чтобы установить их NP-полноту, необходимо связать задачу выполнимости булевой схемы с этим набором задач. Проще всего это было сделать для задачи, с которой у нее больше всего общего: задачей 3-SAT.

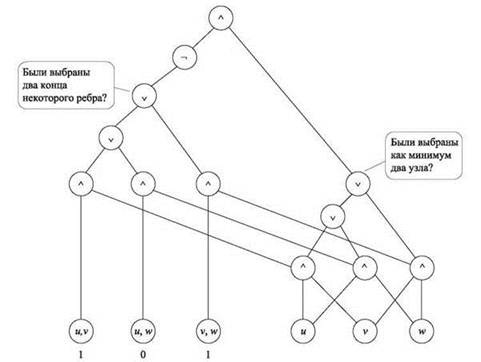
Рис. 8.5. Схема для проверки наличия 2-узлового независимого множества в 3-узловом графе

(8.15) Задача 3-SAT является NP-полной.

Доказательство. Очевидно, задача 3-SAT принадлежит NP, так как мы можем проверить за полиномиальное время, что предложенный вариант присваивания удовлетворяет заданному набору условий. Для доказательства ее NP-полноты будет использоваться сведение SAT≤_Р3-SAT.

Для заданного экземпляра задачи выполнимости булевой схемы мы сначала построим эквивалентный экземпляр SAT, в котором каждое условие содержит не более трех переменных. Затем этот экземпляр SAT будет преобразован в эквивалентный, в котором каждое условие содержит ровно три переменные. Таким образом, последний набор условий будет экземпляром 3-SAT, а следовательно, завершает сведение.

Итак, рассмотрим произвольную булеву схему K. Переменная x_v связывается с каждым узлом v схемы для кодирования логического значения, содержащегося в этом узле схемы. Далее мы определим условия задачи SAT. Сначала нужно закодировать требование о том, что схема правильно вычисляет значение в каждом логическом элементе по входным значениям. Возможны три случая в зависимости от трех типов элементов.

♦ Если узел v помечен операцией ¬ и его единственное входящее ребро выходят из узла u, то должно выполняться Чтобы гарантировать это, мы добавляем два условия:

♦ Если узел v помечен операцией V и два его входящих ребра выходят из узлов u и w, то должно выполняться x_v = x_u V x_w. Чтобы гарантировать это, мы добавляем следующие условия:

♦ Если узел v помечен операцией Λ и два его входящих ребра выходят из узлов u и w, то должно выполняться x_v = x_u Λ x_w. Чтобы гарантировать это, мы добавляем следующие условия:

Наконец, необходимо гарантировать, что константы в источниках имеют указанные значения, а на выходе выдается результат 1. Соответственно для источника v, помеченного константным значением, добавляется условие с одной переменной х_v или под воздействием которого х_v принимает заданное значение. Для выходного узла о добавляется условие с одной переменной х₀, которое требует, чтобы значение о было равно 1. На этом построение завершается.

Не так сложно показать, что только что построенный экземпляр SAT эквивалентен заданному экземпляру задачи выполнимости булевой схемы. Чтобы продемонстрировать эквивалентность, необходимо привести два обоснования. Во-первых, предположим, что заданная схема K выполнима. Выполняющее присваивание входам схемы расширяется для создания значений во всех узлах K (как было сделано в примере на рис. 8.4). Это множество значений очевидным образом обеспечивает выполнимость построенного экземпляра SAT.

Чтобы провести рассуждения в другом направлении, мы предположим, что построенный экземпляр SAT является выполнимым. Рассмотрим выполняющее присваивание в этом экземпляре и значения переменных, соответствующие входам схемы K. Утверждается, что эти значения образуют выполняющее присваивание для схемы K. Чтобы убедиться в этом, достаточно заметить, что условия SAT гарантируют, что значения, присвоенные всем узлам K, совпадают с теми, которые вычисляются схемой для этих узлов. В частности, выходу будет присвоено значение 1, поэтому присваивание значений входам обеспечивает выполнимость K.

Итак, мы показали, как создать экземпляр SAT, эквивалентный задаче выполнимости булевой схемы. Но работа еще не завершена, так как нашей целью является создание экземпляра 3-SAT, который требует, чтобы длина всех условий была равна в точности 3, — а в созданном нами экземпляре некоторые условия имеют длину 1 или 2. Итак, для завершения доказательства необходимо преобразовать этот экземпляр SAT в эквивалентный экземпляр, в котором каждое условие состоит ровно из трех переменных.

Для этого мы введем четыре новые переменные: z₁, z₂, z₃, z₄. Идея заключается в том, чтобы гарантировать, что для каждого выполняющего присваивания z₁ = z₂ = 0; для этого добавляются условия и для i = 1 и i = 2. Обратите внимание: выполнение всех этих условий возможно только в том случае, если z₁ = z₂ = 0.

Теперь рассмотрим условие в построенном экземпляре SAT, которое содержит один литерал t (которым может быть переменная или отрицание переменной). Каждый такой литерал заменяется условием (t V z₁ V z₂). Аналогичным образом каждое условие, содержащее два литерала (допустим, t V t'), заменяется условием (t V t' V z₁). Полученная формула 3-SAT очевидно эквивалентна формуле SAT, содержащей не более трех переменных в каждом условии, что завершает доказательство. ■

Используя этот результат и последовательность сведений

3-SAT ≤_р Независимое множество ≤_р Вершинное покрытие ≤_р Покрытие множества,

мы через (8.14) приходим к следующему выводу:

(8.16) Все следующие задачи являются NР-полными: задача о независимом множестве, задача упаковки множества, задача о вершинном покрытии и задача покрытия множества.

Доказательство. Каждая из этих задач обладает тем свойством, что она принадлежит NP, и задача 3-SAT (а следовательно, и задача SAT) может быть сведена к ней. ■

Общая стратегия доказательства NР-полноты новых задач

В оставшейся части этой главы мы в основном будем заниматься изучением других NP-полных задач. В частности, мы обсудим другие разновидности сложных вычислительных задач и докажем, что некоторые представители этих категорий являются NP-полными. Как упоминалось в начале главы, для этого есть чисто практическая причина: так как широко распространено мнение о том, что Р ≠ NP, идентификация NP-полноты задачи может стать веским признаком того, что задача не может быть решена за полиномиальное время.

Основная стратегия доказательства NP-полноты новой задачи X выглядит примерно так:

1. Доказать, что X ∈ NP.

2. Выбрать задачу Y, которая заведомо является NP-полной.

3. Доказать, что Y≤_рХ.

Ранее было замечено, что многие сведения Y≤_рX состоят из преобразования заданного экземпляра Y в экземпляр X с тем же ответом. Для решения X используется одно обращение к “черному ящику”. При использовании подобных сведений приведенная выше стратегия превращается в следующий план доказательства NP-полноты.

1. Доказать, что X ∈ NP.

2. Выбрать задачу Y, которая заведомо является NP-полной.

3. Рассмотреть произвольный экземпляр s_Y задачи Y и показать, как построить за полиномиальное время экземпляр s_X задачи X, обладающий следующими свойствами.

(a) Если s_Y является экземпляром Y, на который дается ответ “да”, то и s_X является экземпляром X, на который дается ответ “да”.

(b) Если s_X является экземпляром X, на который дается ответ “да”, то и s_y является экземпляром Y, на который дается ответ “да”.

Другими словами, тем самым устанавливается, что s_Y и s_X имеют одинаковый ответ.

Проводились исследования, направленные на изучение различий между сведениями с полиномиальным временем для специальной структуры (обращение к “черному ящику” с одним вопросом и буквальное использование полученного ответа) и более общей концепцией сведения с полиномиальным временем, при которых обращения к “черному ящику” могут производиться многократно. (Более ограниченный вариант сведения называется сведением по Карпу, тогда как более общий вариант называется сведением по Куку или сведением по Тьюрингу с полиномиальным временем.) Здесь эти различия рассматриваться не будут.