Декомпозиция графа в дерево - Расширение пределов разрешимости

В предыдущих двух разделах мы видели, как конкретные NР-сложные задачи (а именно задачи о независимом множестве с максимальным весом и раскраске графа) могут решаться при ограниченной структуре входных данных. Когда вы оказываетесь в такой ситуации — возможности решения NР-полной задачи в более или менее естественном частном случае, — стоит спросить себя, почему этот метод не работает в общем случае. Как упоминалось в разделах 10.2 и 10.3, наши алгоритмы в обоих случаях использовали особенности конкретной разновидности структуры: тот факт, что входные данные можно было разбить на подзадачи с очень ограниченным взаимодействием.

Например, чтобы решить задачу о независимом множестве с максимальным весом для дерева, мы используем специальное свойство (корневых) деревьев: после принятия решения о том, должен ли узел и включаться в независимое множество или нет, подзадачи в каждом поддереве становятся полностью изолированными; мы можем решать каждую из них так, словно остальных не существует. В обобщенных графах, где может не быть узла, “разрывающего связь” между подзадачами в других частях графа, такая удобная возможность отсутствует. В задаче о независимом множестве для обобщенного графа решения, принятые в одном месте, приводят к сложным вторичным эффектам по всему графу.

Итак, мы можем задать себе “ослабленную” версию нашего вопроса: насколько общим должен быть класс графов, чтобы для него можно было использовать концепцию “ограниченного взаимодействия” — рекурсивной фрагментации входных данных с использованием малых множеств узлов — для проектирования эффективных алгоритмов для таких задач, как задача о независимом множестве с максимальным весом?

Как выясняется, существует естественный и обладающий широкими возможностями класс графов, поддерживающих алгоритмы такого типа; фактически такие графы представляют собой “обобщенные деревья”, и по причинам, которые вскоре станут ясны, мы будем называть их графами с ограниченной древовидной шириной. Как и для многих деревьев, многие NР-полные задачи разрешимы для графов с ограниченной древовидной шириной; при этом класс графов с ограниченной древовидной шириной имеет существенное практическое значение, потому что к нему относятся многие реальные сети, в которых возникают NР-полные задачи графов. Итак, в каком-то смысле этот тип графов служит примером нахождения “правильного” частного случая задачи, который одновременно позволяет построить эффективный алгоритм и включает графы, встречающиеся на практике.

В этом разделе мы определим понятие древовидной ширины, а также предоставим общий подход к решению задач на графах с ограниченной древовидной шириной. В следующем разделе речь пойдет о том, как определить, имеет ли заданный граф ограниченную древовидную ширину.

Определение древовидной ширины

Дадим точное определение класса графов, предназначенного для обобщенного представления деревьев. В основу определения заложены два соображения. Во-первых, нам нужны графы, которые можно разложить на несвязанные части удалением небольшого количества узлов; это позволит реализовать динамические алгоритмы того типа, о котором говорилось ранее. Во-вторых, мы хотим формализовать интуитивное представление о “древовидных” изображениях графов наподобие изображенного на рис. 10.5, b.

Нам хотелось бы утверждать, что граф G, изображенный на рисунке, может быть разложен в древовидный формат по упомянутым выше соображениям. Если взглянуть на граф G в том виде, в каком он изображен на рис. 10.5, вероятно, не будет очевидно, что это возможно. Но из рис. 10.5, b видно, что G на самом деле состоит из десяти переплетенных треугольников; и семь из десяти треугольников обладают тем свойством, что при их удалении остаток G распадется на несвязанные части, рекурсивно обладающие той же структурой из сцепленных треугольников. Еще три треугольника прикреплены в крайних точках, и их удаление можно сравнить с удалением листовых узлов из дерева.

Итак, граф G древовиден, если рассматривать его не как состоящий из двенадцати узлов, как обычно, а как состоящий из десяти треугольников. И хотя G очевидным образом содержит много циклов, при рассмотрении на уровне этих десяти треугольников циклов словно бы и нет; на этом основании граф наследует многие полезные декомпозиционные свойства дерева.

Древовидная структура из треугольников должна представляться так, чтобы каждый треугольник соответствовал узлу дерева, как показано на рис. 10.5, с. Интуитивно понятно, что дерево на рисунке соответствует графу (каждый узел дерева представляет один из треугольников). Однако обратите внимание на то, что одни узлы графа присутствуют в разных треугольниках — даже в треугольниках, не являющихся смежными в структуре дерева, и некоторые ребра соединяют узлы треугольников, находящихся очень далеко в древовидной структуре, — например, центральный треугольник соединяется ребрами с узлами всех остальных треугольников. Как точно сформулировать соответствие между деревом и графом? Для этого мы введем понятие древовидной декомпозиции графа G, которая называется так потому, что мы хотим провести декомпозицию G по древовидной схеме.

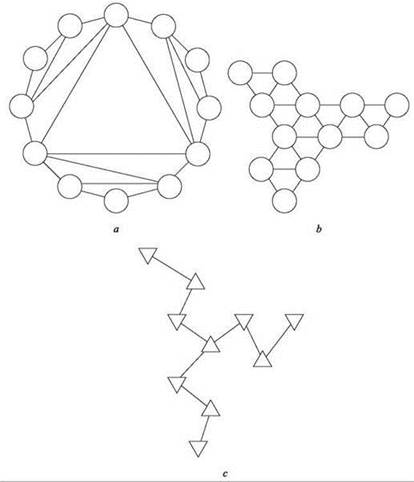
Рис. 10.5. На рисунке а и b изображен один граф в разных представлениях. Рисунок b подчеркивает, что граф состоит из десяти сплетенных треугольников. На рисунке c схематично показано, как эти треугольники “сцепляются” друг с другом

Формально декомпозиция G = (V, E) состоит из дерева T (множество узлов которого отличается от G) и подмножества V_t ⊆ V, связанного с каждым узлом t дерева T (мы будем называть эти подмножества V_t “фрагментами” декомпозиции). Иногда мы будем записывать ее в виде упорядоченной пары (T,{V_t: t ∈ T}). Дерево T и множество фрагментов {V_t: t ∈ T} должны удовлетворять следующим трем условиям:

♦ (покрытие узлов): каждый узел G принадлежит минимум одному фрагменту V_t;

♦ (покрытие ребер): для каждого ребра е графа G, существует фрагмент V_t, содержащий оба конца е;

♦ (согласованность): пусть t₁, t₂ и t₃ — такие три узла Т, что t₂ лежит на пути из t₁ в t₃. Если узел v графа G принадлежит как так и то он также принадлежит

Следует заметить, что дерево на рис. 10.5, c является древовидной декомпозицией графа, которая использует десять треугольников в качестве фрагментов.

Теперь рассмотрим случай, при котором граф G является деревом. Древовидная декомпозиция строится следующим образом: декомпозиционное дерево T содержит узел t_v для каждого узла vграфа G и узел t_e для каждого ребра e графа G. Дерево T содержит ребро (t_v, t_e), где v — конец e. Наконец, если v является узлом, мы определяем фрагмент а если е = (u, v) — ребро, то определяется фрагмент Теперь мы можем убедиться в том, что три свойства определения древовидной декомпозиции выполнены.

Свойства декомпозиции

Присмотревшись к определению, мы видим, что свойства покрытия узлов и ребер просто гарантируют минимальное соответствие между набором фрагментов и графом G. Важнейшим аспектом определения является свойство согласованности. Хотя из его формулировки не очевидно, что согласованность приводит к свойствам древовидного разбиения, на самом деле это происходит вполне естественным образом. Деревья обладают двумя полезными и очень часто используемыми свойствами разбиения, которые тесно связаны друг с другом. Одно свойство утверждает, что при удалении ребра e дерево распадается ровно на две компоненты связности. Другое свойство утверждает, что при удалении узла t из дерева с последующим удалением всех инцидентных ему ребер дерево распадается на компоненты, число которых равно степени t. Свойство согласованности гарантирует, что разбиения T обоего типа имеют естественное соответствие среди разбиений G.

Если T' — подграф T, мы будем использовать обозначение G_T, для подграфа G, определяемого всеми узлами всех фрагментов, связанных с узлами T', то есть множества U_t∈TV_t.

Для начала рассмотрим удаление узла t из T.

(10.13) Предположим, T - t содержит компоненты T₁, ..., T_d. В этом случае подграфы

не имеют общих узлов и не соединяются ребрами.

Доказательство. На рис. 10.6 показано, как примерно выглядит разбиение. Сначала мы докажем, что подграфы не имеют общих узлов. В самом деле, любой такой узел v должен принадлежать как так и для некоторого i ≠ j, поэтому такой узел v принадлежит некоторому фрагменту V_x для x ∈ T_i, и некоторому фрагменту V_y для y ∈ T_j. Так как t лежит на пути x-y в T, из свойства согласованности следует, что v лежит в V_t, а следовательно, не принадлежит ни ни

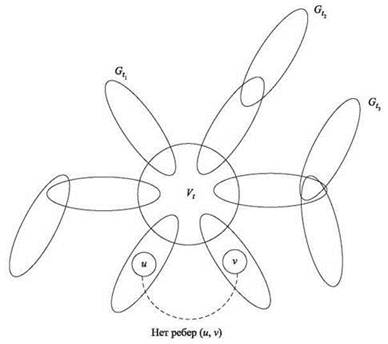
Рис. 10.6. Разбиения дерева T преобразуются в разбиения графа G

Затем мы должны показать, что в G нет ребра е = (u, v), один конец которого u принадлежит подграфу а другой конец v принадлежит подграфу для некоторого j ≠ i. Если бы такое ребро существовало, то по свойству покрытия ребер должен был существовать фрагмент V_x, соединяющий u и v. Узел х не может входить одновременно в подграфы Т_i и Т_j. Допустим, с учетом симметрии X ∈ Т_i. Узел u принадлежит подграфу поэтому узел u должен принадлежать множеству V_y для некоторого y в T_i. Тогда узел u принадлежит как V_x, так и V_y, а поскольку t лежит на пути х-у в Т, из этого следует, что u также принадлежит V_t, поэтому он не лежит в как и требовалось. ■

Свойство разбиения по ребрам доказывается аналогично. Если удалить ребро (x, у) из T, то T разбивается на две компоненты: X (содержит х) и Y (содержит Y). Установим соответствующий способ разбиения G этой операцией.

(10.14) Пусть X и Y — две компоненты T после удаления ребра (х, у). Тогда удаление множества V_x ∩ V_y из V разбивает G на два подграфа G_X - (V_x ∩ V_y) и G_Y - (V_x ∩ V_y). А точнее, эти два подграфа не имеют общих узлов и не существует ребра, один конец которого принадлежал бы каждому из них.

Доказательство. Общая схема разбиения изображена на рис. 10.7. Доказательство этого свойства аналогично доказательству (10.13). Сначала мы доказываем, что два подграфа G_X - (V_x ∩ V_y) и G_Y - (V_x ∩ V_y) не имеют общих узлов, показывая, что узел v, который принадлежит как G_X, так и G_Y, должен принадлежать как V_x, так и V_y, а следовательно, он не входит ни в G_Y - (V_x ∩ V_y), ни в G_X - (V_x ∩ V_y).

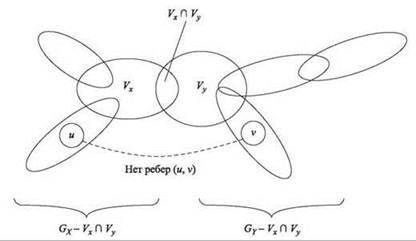
Рис. 10.7. Удаление ребра дерева T преобразуется в разбиение графа G

Теперь нужно показать, что в G не существует ребра e = (u, v), один конец которого и принадлежит G_X - (V_x ∩ V_y), а другой конец v принадлежит G_Y - (V_x ∩ V_y). Если бы такое ребро существовало, то по свойству покрытия ребер должен существовать фрагмент V_z, содержащий u и v. Допустим, с учетом симметрии z ∈ X. Узел v также принадлежит некоторому фрагменту V_wдля w ∈ Y. Поскольку x и у лежат на пути w-z в T, из этого следует, что V принадлежит V_x и V_y. Следовательно, v ∈ V_x ∩ V_y не принадлежит G_Y - (V_x ∩ V_y), как и требуется. ■

Итак, древовидные декомпозиции полезны тем, что свойства разбиения T переносятся на G. Возможно, кому-то покажется, что дальше нужно найти ответ на ключевой вопрос: какие графы имеют древовидные декомпозиции? Но в действительности это не так, потому что если подумать, станет ясно, что у любого графа существует древовидная декомпозиция. Для любого графа Gможно выбрать в качестве T дерево, состоящее из одного узла t, а единственным фрагментом V_t назначить все множество узлов G. Такое определение легко выполняет три свойства, требуемых в определении; тем не менее пользы от такой декомпозиции ничуть не больше, чем от исходного графа.

Следовательно, важно найти древовидную декомпозицию, в которой все фрагменты малы. Именно это свойство мы пытаемся перенести с деревьев, требуя, чтобы удаление очень малых множеств узлов разбивало граф на несвязные подграфы. Соответственно мы определяем ширину древовидной декомпозиции (T, {V_t}) на 1 менее максимального размера любого фрагмента V_t:

Древовидная ширина G определяется как минимальная ширина любой древовидной декомпозиции G. Из-за свойства покрытия ребер все древовидные декомпозиции должны содержать фрагменты не менее чем с двумя узлами, а следовательно, иметь древовидную ширину не менее 1. Вспомните, что наша древовидная декомпозиция для дерева G имеет ширину 1, так как каждое из множеств V_t содержит либо один, либо два узла. Несколько странное “-1” в этом определении нужно для того, чтобы деревья имели ширину 1 вместо 2. Кроме того, все графы с нетривиальной декомпозицией, обладающие древовидной шириной w, имеют разделители с размером w, потому что если (x, у) — ребро дерева, согласно (10.14), удаление V_x ∩ V_y разбивает Gна две компоненты.

Итак, мы можем говорить о множестве всех графов с древовидной шириной 1, множестве всех графов с древовидной шириной 2 и т. д. Следующий факт устанавливает, что из всех графов только деревья имеют древовидную ширину 1, а следовательно, наши определения действительно обобщают концепцию дерева. Доказательство также предоставляет хорошую возможность для проявления некоторых базовых свойств декомпозиций. Также заметим, что граф на рис. 10.5 в соответствии с определением древовидной ширины относится ко второму по “простоте” классу графов после деревьев: это граф с древовидной шириной 2.

(10.15) Древовидная ширина связного графа G равна 1 в том, и только в том случае, если он является деревом.

Доказательство. Ранее уже было показано, что если граф G является деревом, то для него можно построить декомпозицию с древовидной шириной 1.

Чтобы доказать обратное, сначала заметим один полезный факт: если H — подграф G, то древовидная ширина H не превышает древовидной ширины G. Это доказывается хотя бы тем, что для заданной декомпозиции (T, {V_t}) графа G можно определить декомпозицию H с тем же деревом T, заменив каждый фрагмент V_t на V ∩ H. Легко проверить, что три обязательных свойства продолжают выполняться. (Тот факт, что некоторые фрагменты могут быть равны пустому множеству, не создает проблем.)

Теперь предположим от противного, что G — связный граф с древовидной шириной 1, который не является деревом. Так как G не является деревом, он содержит подграф, состоящий из простого цикла C. Из предыдущего абзаца следует, что теперь нам достаточно доказать, что граф C не имеет древовидной ширины 1. В самом деле, предположим, что у него существует декомпозиция (T, {V_t}), в которой каждый фрагмент имеет размер не более 2. Выберем любые два ребра (u, v) и (u', v') в C; по свойству покрытия ребер существуют содержащие их фрагменты V_t и V_t'. На пути в T из t в t' должно существовать такое ребро (x, у), что фрагменты V_x и V_y не равны. Из этого следует, что |V_x ∩ V_y| ≤ 1. Теперь мы воспользуемся (10.14): определяя X и Y как компоненты T - (x, у), содержащие x и у соответственно, мы видим, что удаление V_x ∩ V_y разделяет C на C_X - (V_x ∩ V_y) и C_Y - (V_x ∩ V_y). Ни один из этих двух подграфов не может быть пустым, так как один содержит {u, v} - (V_x ∩ V_y), а другой содержит {u', v'} - (V_x ∩ V_y). Но цикл невозможно разбить на два непустых подграфа удалением всего одного узла, поэтому мы приходим к противоречию. ■

Применяя декомпозицию в контексте алгоритмов динамического программирования, по соображениям эффективности было бы желательно, чтобы количество фрагментов было относительно небольшим. Этого можно добиться простым способом: если имеется древовидная декомпозиция (T, {V_t}) графа G и в T имеется такое ребро (x, у), что V_x ⊆ V_y, то мы можем свернуть ребро (x, у) (“складывая” фрагмент V_x в V_y) и получить декомпозицию G для меньшего дерева. Повторяя этот процесс необходимое количество раз, мы получим древовидную декомпозицию без избыточности: в полученном дереве не существует такого ребра (x, y), что V_x ⊆ V_y.

После получения декомпозиции можно проверить, что она не содержит слишком большого количества фрагментов:

(10.16) Любая неизбыточная древовидная декомпозиция n-узлового графа содержит не более n узлов.

Доказательство. Мы воспользуемся индукцией по n; случай n = 1 очевиден. Рассмотрим случай n > 1. Для имеющейся декомпозиции (T{V_t}) n-узлового графа без избыточности мы сначала найдем лист t в T. Согласно условию неизбыточности, в V_t должен быть как минимум один узел, не входящий в соседний фрагмент, а значит (по свойству согласованности), не входящий в любой другой фрагмент. Пусть U — множество таких узлов в V_t. Заметим, что при удалении t из T и удалении V_t из множества фрагментов будет получена древовидная декомпозиция G-U без избыточности. Согласно индукционной гипотезе, эта декомпозиция имеет не более n - |U| ≤ n - 1 фрагментов, поэтому (T, {V_t}) содержит не более n фрагментов. ■

Хотя (10.16) помогает убедиться в том, что древовидная декомпозиция относительно невелика, чаще в процессе анализа графа проще начать с построения избыточной декомпозиции, чтобы позднее “сжать” ее до неизбыточной. Например, наша декомпозиция графа G, который представляет собой дерево, строит избыточный результат; с ходу описать неизбыточную декомпозицию было бы не так просто.

Итак, фундамент заложен, и мы можем обратиться к алгоритмическим применениям древовидных декомпозиций.

Динамическое программирование и древовидная декомпозиция

Мы начали с утверждения о том, что задача о независимом множестве с максимальным весом может быть эффективно решена для любого графа с ограниченной древовидной шириной. Пришло время выполнить обещание, а именно: мы разработаем алгоритм, который точно следует алгоритму с линейным временем для деревьев. Для заданного n-узлового графа, с которым связана древовидная декомпозиция с шириной w, этот алгоритм выполняется за время O(f(w) ∙ n), где f(∙) — экспоненциальная функция, которая зависит только от ширины w, а не от количества узлов n. И хотя мы будем заниматься задачей о независимом множестве с максимальным весом, как и в случае с деревьями, примененный метод пригодится при решении многих NP-сложных задач.

Итак, в очень конкретном смысле сложность задачи была переведена из размера графа в древовидную ширину, которая может быть намного меньше. Как упоминалось ранее, большие сети в реальном мире часто имеют очень малую древовидную ширину; и часто эта особенность проявляется не случайно, а вследствие структурированного или модульного подхода к их планированию. Итак, если вы имеете дело с сетью из 1000 узлов с древовидной декомпозицией ширины 4, рассматриваемый метод позволяет преобразовать безнадежно неразрешимую задачу в потенциально выполнимую.

Конечно, ситуация отчасти напоминает алгоритм вершинного покрытия из раздела 10.1. Тогда экспоненциальная сложность была переведена в параметр k, размер искомого вершинного покрытия. На этот раз очевидного параметра, кроме n, не видно, поэтому нам пришлось изобрести неочевидный: древовидную ширину.

Чтобы разработать алгоритм, вспомним, что было сделано в случае дерева T. После определения корня T мы построили независимое множество, двигаясь вверх от листьев. В каждом внутреннем узле и мы перебираем возможные решения относительно узла u (включать или не включать), так как после фиксирования этого решения задачи разных поддеревьев под uстановятся независимыми.

Обобщение для графа G с древовидной декомпозицией (T, {V_t}) ширины w выглядит очень похоже. Мы закрепляем корень T и строим независимое множество, рассматривая фрагменты V_t от листьев вверх. Во внутреннем узле t из T мы сталкиваемся со следующим основным вопросом: оптимальное независимое множество пересекает фрагмент V_t в некотором подмножестве U, но мы не знаем, какое это множество U. Соответственно мы перебираем все возможности для этого подмножества U, то есть все возможности относительно того, какие узлы из V_t включать, а какие не включать. Поскольку V_t может иметь размер до w + 1, появляется до 2^w+1 рассматриваемых возможностей. Но теперь можно использовать два ключевых факта: во-первых, величина 2^w+1намного разумнее 2ⁿ, когда w намного меньше n; и во-вторых, после фиксирования конкретной возможности 2^w+1 (когда мы решим, какие узлы в фрагменте V_t будут включены), свойства разбиения (10.13) и (10.14) гарантируют, что задачи разных поддеревьев T под могут решаться независимо. Таким образом, хотя мы довольствуемся поиском “грубой силы” на уровне одного фрагмента, в целом алгоритм достаточно эффективно работает на глобальном уровне при малом количестве отдельных фрагментов.

Определение подзадач

Корень дерева Т помещается в узел r. Для любого узла t обозначим T_t поддерево с корнем t. Вспомните, что обозначает подграф G, сформированный узлами всех фрагментов, ассоциированных с узлами T_t; для упрощения записи мы будем обозначать этот подграф G_t. Для подмножества U множества F общий вес узлов в U будет обозначаться w(U); то есть

Для каждого поддерева T_t определяется множество подзадач, соответствующих каждому возможному подмножеству U множества V_t, которое может представлять пересечение оптимального решения с V_t. Таким образом, для каждого независимого множества U ⊆ V_t мы используем запись f_t(U) для обозначения максимального веса независимого множества S в G_t, соответствующего требованию S ∩ V_t = U. Величина f_t(U) не определена, если U не является независимым множеством, поскольку в этом случае известно, что U не может представлять пересечение оптимального решения с V_t.

С каждым узлом t дерева T может быть связано не более 2^w+1 подзадач, так как это максимально возможное число независимых подмножеств V_t. Согласно (10.16) можно считать, что мы работаем с древовидной декомпозицией, имеющей не более n фрагментов; следовательно, общее количество подзадач не превышает 2^w+1n. Очевидно, при наличии решений всех этих подзадач максимальный вес независимого множества в G можно определить по подзадачам, связанным с корнем г: нужно просто взять максимум по всем независимым множествам U ⊆ V_r из f_r(U).

Построение решений

Теперь мы должны показать, как строить решения этих подзадач посредством рекурсии. Начать несложно: когда t является листом, f_t(U) равно w(U) для каждого независимого множества U ⊆V_t.

Предположим, что дочерние узлы t обозначены t₁, ..., t_d и мы уже определили значения для каждого дочернего узла t_i и каждого независимого множества Как определить значение f_t(U) для независимого множества U ⊆ V_t?

Пусть S — независимое множество с максимальным весом в G_t, для которого S ∩ V_t = U; то есть w(S) = f_t(U). Важно понять, как выглядит это множество S при пересечении с каждым из подграфов (рис. 10.8). Обозначим S_f пересечение S_i с узлами

(10.17) S_i является независимым множеством с максимальным весом для при условии, что

Доказательство. Предположим, существует независимое множество S'_i, для с тем свойством, что и w(S'_i) > w(S_i). Тогда рассмотрим множество S' = (S - S_i) U S'_i. Очевидно, w(S') > w(S). Также легко убедиться в том, что S' ∩ V_t = U.

Утверждается, что S' является независимым множеством в G; это будет противоречить нашему выбору S как независимого множества с максимальным весом в G_t, соответствующего условию S ∩V_t = U. Например, предположим, что S' не является независимым; пусть e = (u, v) — ребро, оба конца которого принадлежат S'. Однако u и v одновременно S принадлежать не могут, иначе они будут принадлежать S'_i, так как оба являются независимыми множествами. Следовательно, u ∈ S - S'_i и v ∈ S'_i - S, из чего следует, что u не является узлом a Но тогда согласно (10.14) не может быть ребра, соединяющего u и v. ■

Утверждение (10.17) — именно то, что необходимо для определения рекуррентного отношения для подзадач. Оно сообщает, что информация, необходимая для вычисления f_t(U), неявно содержится в значениях, уже вычисленных для поддеревьев. А именно: для всех дочерних t_i достаточно просто определить значение независимого множества с максимальным весом S_i для с учетом ограничения Это ограничение не определяет точно, что собой представляет оно лишь говорит, что это может быть любое независимое множество для которого Следовательно, вес оптимального варианта S_i равен

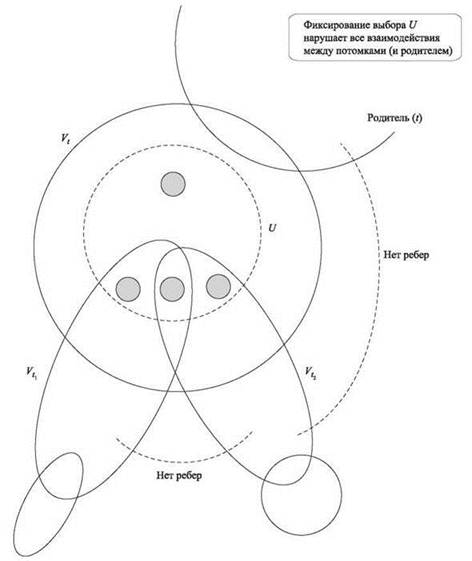
Рис. 10.8. Подзадача f_t(U) в подграфе G_t. В оптимальном решении этой подзадачи мы рассматриваем независимые множества S_i в подграфах-потомках для которых

Наконец, значение f_t(U) равно просто w(U) в сумме с максимумами, добавленными по d дочерним узлам t, — не считая того, что для предотвращения повторного подсчета узлов U мы исключаем их из вклада дочерних узлов. Таким образом:

(10.18) Значение f_t(U) задается следующим рекуррентным отношением:

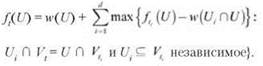
Обобщенный алгоритм просто строит значения всех подзадач по листьям T и вверх.

Как обычно, независимое множество с максимальным весом находится обратным отслеживанием по последовательности выполнения.

Время, необходимое для вычисления f_t(U), находится следующим образом: для каждого из d дочерних узлов t_i и для каждого независимого множества U_i в мы за время O(w) проверяем условие чтобы узнать, должно ли оно рассматриваться при вычислении (10.18).

Для f_t(U) общее время составляет O(2^w+1wd); так как с t связано не более 2^w+1 множеств U, общие затраты времени на узел t составляют O(4^w+1wd). Наконец, эти величины суммируются по всем узлам t для получения общего времени выполнения. Мы видим, что сумма по всем узлам t количества дочерних узлов t равна O(n), так как каждый узел считается как дочерний один раз. Следовательно, общее время выполнения составляет O(4^w+1wn).