Покрытие множества: обобщенная жадная эвристика - Аппроксимирующие алгоритмы

В этом разделе рассматривается общая задача, которая уже встречалась в главе 8, — задача покрытия множества. Некоторые важные алгоритмические задачи формулируются как особые случаи задачи покрытия множества, поэтому аппроксимирующий алгоритм для этой задачи найдет широкое применение. Мы покажем, что возможно разработать жадный алгоритм, который создает решения с гарантированным коэффициентом аппроксимации относительно оптимума, хотя этот коэффициент будет слабее тех, что мы видели в задачах из разделов 11.1 и 11.2.

Хотя жадный алгоритм, который мы построим для задачи покрытия множества, будет очень простым, его анализ сложнее приводившегося в двух предыдущих разделах. Тогда мы могли обойтись очень простыми границами для (неизвестного) оптимального решения, тогда как здесь задача сравнения с оптимумом более сложна, и нам потребуются более сложные границы. Этот аспект метода можно рассматривать как первый пример метода назначения цены, который будет более полно рассмотрен в двух следующих разделах.

Задача

Как вы помните из главы, посвященной NР-полноте, задача покрытия множества базируется на множестве U из n элементов и списке S₁, ..., S_m подмножеств U; покрытием множестваназывается совокупность этих множеств, объединение которых равно всему множеству U.

В версии задачи, которая рассматривается здесь, с каждым множеством S_i вес w_i ≥ 0. Требуется найти покрытие множества C с минимальным общим весом

Стоит заметить, что по сложности эта задача по крайней мере не уступает версии задачи покрытия множества с принятием решения, которая встречалась ранее; если назначить все w_i = 1, то минимальный вес покрытия множества не превосходит k в том, и только в том случае, если существует совокупность не более чем k множеств, покрывающая U.

Разработка алгоритма

Мы разработаем и проанализируем жадный алгоритм для этой задачи. Алгоритм должен обладать тем свойством, что он строит покрытие по одному множеству; чтобы выбрать следующее множество, он ищет то, которое, насколько можно судить, обеспечивает наибольший прогресс по направлению к цели. Как естественно определить “прогресс” в этой конфигурации? Предпочтительные множества обладают двумя свойствами: они имеют малый вес w_i и покрывают много элементов. Тем не менее ни одного из этих свойств в отдельности не достаточно для построения хорошего алгоритма аппроксимации. Вместо этого будет естественно объединить эти два критерия в одну метрику w_i/|S_i|: то есть, выбирая S_i, мы покрываем |S_i| элементов за стоимость w_i; соответственно это отношение определяет условную “цену покрытия элемента” — весьма разумная метрика для выбора.

Конечно, после того, как некоторые множества уже были выбраны, нас интересует лишь то, что происходит с еще не покрытыми элементами. Соответственно мы будем вести множество Rоставшихся непокрытых элементов и выберем множество S_i, минимизирующее w_i/|S_i ∩ R|.

Пример поведения этого алгоритма представлен на рис. 11.6. Сначала алгоритм выбирает множество из четырех нижних узлов (так как оно имеет лучшее отношение вес/покрытие 1/4). Затем выбирается множество, состоящее из двух узлов во второй строке, и, наконец, множество из двух отдельных узлов наверху. Таким образом, будет выбрана совокупность множество с общим весом 4. Так как алгоритм каждый раз “близоруко” выбирает лучший вариант, он упускает тот факт, что все узлы можно покрыть с весом всего 2 + 2ε — для этого достаточно выбрать два множества, каждое из которых покрывает целый столбец.

Анализ алгоритма

Множества, выбираемые алгоритмом, очевидно образуют покрытие. Нас интересует вопрос: насколько вес этого покрытия превышает вес w* оптимального покрытия?

Как и в разделах 11.1 и 11.2, для нашего анализа потребуется хорошая нижняя граница оптимума. В задаче о распределении нагрузки мы использовали нижние границы, которые естественно вытекали из постановки задачи: среднюю нагрузку и максимальный размер задания. Задача о покрытии множества оказывается более сложной; “простые” нижние границы не особенно полезны, вместо них мы используем нижнюю границу, которая неявно строится жадным алгоритмом и является своего рода “побочным результатом”.

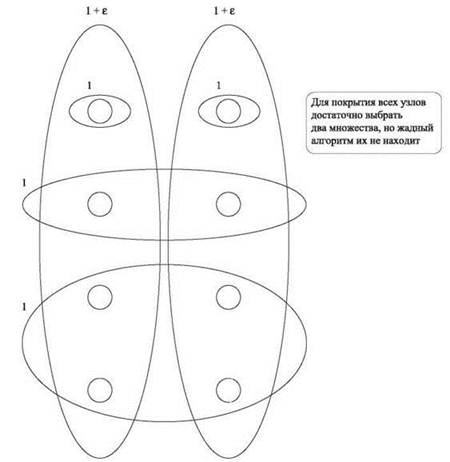
Рис. 11.6. Экземпляр задачи покрытия множества, в котором веса множеств равны либо 1, либо 1 + ε для некоторого малого ε > 0. Жадный алгоритм выбирает множества с общим весом 4 вместо оптимального решения с весом 2 + 2ε

Вспомните интуитивный смысл отношения w_i/|S_i ∩ R|, используемого алгоритмом, — это “стоимость”, выплачиваемая за покрытие каждого нового элемента. Сохраним эту стоимость, выплаченную за элемент s, в величине c_s. Добавим следующую строку в алгоритм сразу же после выбора множества S_i:

Определить c_s = w_i/|S_i ∩ R| для всех s ∈ S_i ∩ R

Значения c_s никак не влияют на поведение алгоритма; это своего рода промежуточный результат, который упрощает сравнение с оптимальным w*. При выборе каждого множества S_i его вес распределяется по стоимостям c_s последних покрытых элементов. Таким образом, эти стоимости отражают общий вес покрытия множества, и мы имеем

(11.9) Если С — покрытие множества, построенное процедурой Greedy-Set-Cover, то

Ключевую роль в анализе играет следующий вопрос: за какую общую стоимость может “отвечать” любое отдельное множество S_k, другими словами, предоставление границы для относительно веса w_k множества (даже для множеств, не выбранных жадным алгоритмом). Определение для отношения

верхней границы, выполняемой для каждого множества, фактически означает: “Чтобы покрыть большую стоимость, необходимо использовать большой вес”. Мы знаем, что оптимальное решение должно покрывать полную стоимость через выбранные им множества; следовательно, граница такого типа устанавливает, что оно должно использовать по крайней мере некоторую величину веса. Это нижняя граница оптимума, что и требуется для нашего анализа.

В нашем анализе будет использоваться гармоническая функция

Чтобы понять ее асимптотический размер как функцию n, можно интерпретировать ее как сумму, аппроксимирующую область под кривой у = 1/х. На рис. 11.7 показано, как она естественно ограничивается сверху и снизу Следовательно, мы видим, что H(n) = Ө(ln n).

Рис. 11.7. Верхняя и нижняя границы для гармонической функции H(n)

Следующее утверждение является ключевым для установления границы для производительности алгоритма.

(11.10) Для каждого множества S_k сумма не превышает H(|S_k|) ∙ w_k.

Доказательство. Для упрощения записи будем считать, что элементами S_k являются первые d = |S_k| элементов множества U, то есть S_k = {s₁, ..., s_d}. Кроме того, предположим, что эти элементы следуют в порядке назначения им стоимости жадным алгоритмом (с произвольной разбивкой “ничьих”). Такие допущения не приводят к потере общности, так как речь идет о простом переименовании элементов U.

Теперь рассмотрим итерацию, в которой элемент s_j покрывается жадным алгоритмом для некоторого j ≤ d. В начале этой итерации s_j, s_j+1, ..., s_d ∈ R в соответствии с нашей пометкой элементов. Из этого следует, что |S_k ∩ R| не меньше d - j + 1, а средняя стоимость множества S_k не превышает

Обратите внимание: это не обязательно равенство, так как элемент s_j может быть покрыт в той же итерации, что и некоторые другие элементы s'_j для j' < j. В этой итерации жадный алгоритм выбрал множество S_i c минимальной средней стоимостью; следовательно, средняя стоимость этого множества S_i не превышает среднюю стоимость S_k. Средняя стоимость S_i присваивается s_j, поэтому мы имеем

Теперь просто просуммируем все эти неравенства для всех элементов s ∈ S_k:

А теперь завершим план по использованию границы из (11.10) для сравнения покрытия множества жадного алгоритма с оптимальным. Обозначив d* = max_i|S_i| максимальный размер любого множества, мы приходим к следующему результату аппроксимации:

(11.11) Вес покрытия C, выбранного процедурой Greedy-Set-Cover, превышает оптимальный вес w* не более чем в H(d*) раз.

Доказательство. Пусть С* — оптимальное покрытие множества, такое что Для каждого из множеств в С* из (11.10) следует

Так как эти множества образуют покрытие множества, имеем

Объединяя с (11.9), получаем искомую границу:

Тогда асимптотически граница из (11.11) говорит, что жадный алгоритм находит решение с коэффициентом O(log d*) от оптимального. Так как максимальный размер множества d* может выражаться как постоянная доля от общего количества элементов n, верхняя граница для худшего случая равна O(log n). Однако выражение границы в контексте d* показывает, что если самое большое множество мало, ситуация значительно улучшается.

Интересно заметить, что эта граница фактически является лучшей из возможных, так как существуют экземпляры, в которых жадный алгоритм работает плохо. Чтобы понять, откуда берутся такие экземпляры, снова рассмотрим пример на рис. 11.6. Предположим, он обобщен так, что базовое множество элементов U состоит из двух высоких столбцов, каждый из которых содержит n/2 элементов. Два множества, каждое из которых имеет вес 1 + ε (для некоторого малого ε > 0), покрывают каждый из столбцов по отдельности. Также создадим Ө(log n) множеств, которые обобщают структуру других множеств на схеме: одно множество покрывает нижние n/2 узлов, другое покрывает следующие n/4, третье покрывает следующие n/8 и т. д. Каждое из этих множеств имеет вес 1.

Теперь жадный алгоритм в процессе поиска решения с весом Ө(log n) будет выбирать множества размера n/2, n/4, n/8, ... . С другой стороны, выбор двух множеств, покрывающих столбцы, дает оптимальное решение с весом 2 + 2ε. При помощи более сложных конструкций можно усилить пример до получения экземпляров, в которых жадный алгоритм дает вес, очень близкий к произведению оптимального веса и Н(n). И еще более сложными средствами было показано, что ни один аппроксимирующий алгоритм с полиномиальным временем не может достичь границы аппроксимации, намного лучшей оптимума, умноженного на Н(n), если только не окажется, что P = NP.