Снова о распределении нагрузки: более сложное применение LP - Аппроксимирующие алгоритмы

В этом разделе рассматривается более общая задача распределения нагрузки. Мы разработаем аппроксимирующий алгоритм по той же общей схеме, как и в случае с 2-аппроксимацией, только что разработанной для вершинного покрытия: мы решаем соответствующую задачу линейного программирования, а затем округляем решение. Впрочем, алгоритм и его анализ будут гораздо более сложными, чем требовалось для вершинного покрытия. Как выясняется, экземпляр задачи линейного программирования, который придется решать, по сути, является задачей потока в сети. Используя этот факт, мы сможем гораздо лучше понять, как выглядят нецелые решения задач линейного программирования, и применить это понимание для правильного округления. Для этой задачи единственный аппроксимирующий алгоритм с постоянным множителем основан на округлении решения задачи линейного программирования.

Задача

В этом разделе рассматривается важное естественное обобщение задачи распределения нагрузки, с которой началось наше знакомство с аппроксимирующими алгоритмами. Как тогда, так и сейчас имеется множество J из n заданий, множество M из m машин, и требуется назначить каждое задание некоторой машине, чтобы максимальная нагрузка по любой машине была как можно меньше. В простой задаче распределения нагрузки, рассматривавшейся ранее, каждое задание j могло быть назначено любой машине i. В новом варианте множество машин, рассматриваемых для каждого задания, может быть ограничено; иначе говоря, для каждого задания существует подмножество машин, на которых оно может быть размещено. Это ограничение возникает естественным образом во многих ситуациях: например, при стремлении к распределению нагрузки так, чтобы каждое задание должно назначаться на физически близкую машину или на машину, обладающую необходимыми полномочиями для обработки задания.

В формальном выражении у каждого задания j имеется фиксированный заданный размер t_j ≥ 0 и множество машин M_j ⊆ M, на которые оно может быть назначено. Множества M_j определяются полностью произвольно.

Распределение заданий между машинами называется действительным, если каждое задание j назначается на машину i ∈ M_j. Цель, как и прежде, заключается в минимизации максимальной нагрузки на любой машине: используя запись J_i ⊆ J для обозначения заданий, назначенных на машину i ∈ M в действительном распределении, и запись для обозначения итоговой нагрузки, мы стремимся минимизировать max_iL_i. Полученная формулировка является определением обобщенной задачи распределения нагрузки.

Кроме включения исходной задачи распределения нагрузки как частного случая (в котором M_j = M для всех заданий j), обобщенная задача распределения нагрузки также включает задачу о двудольном идеальном паросочетании как другой частный случай. В самом деле, для двудольного графа с одинаковым количеством узлов на каждой стороне узлы в левой части могут рассматриваться как задания, а узлы в правой части — как машины; мы определяем t_j = 1 для всех заданий j и определяем M_j как множество узлов i, для которых существует ребро (i, j) ∈ E. Распределение с максимальной нагрузкой 1 существует в том, и только в том случае, если в двудольном графе существует идеальное паросочетание. (А следовательно, методы нахождения потока в сети могут использоваться для нахождения оптимальной нагрузки в этом конкретном случае.) Тот факт, что обобщенная задача распределения нагрузки включает обе эти задачи как частные случаи, дает некоторое представление о трудности разработки алгоритма для нее.

Разработка и анализ алгоритма

Разработка аппроксимирующего алгоритма основана на применении линейного программирования для обобщенной задачи распределения нагрузки. Базовый план остается тем же, что и в предыдущем разделе: сначала мы сформулируем задачу как эквивалентную задачу линейного программирования, в которой переменные принимают конкретные дискретные значения; затем мы ослабим ее до задачи линейного программирования, сняв это требование к значениям переменных; и наконец, полученное дробное назначение будет использовано для получения распределения, близкого к оптимальному. При округлении решения для получения распределения нам придется действовать осторожнее, чем в случае с задачей о вершинном покрытии.

Формулировки целочисленного и линейного программирования

Сначала мы сформулируем обобщенную задачу распределения нагрузки как задачу линейного программирования с ограничениями на значения переменных. В формулировке будут использоваться переменные х_ij, соответствующие каждой паре (i, j) из машины i ∈ М и задания j ∈ J. Присваивание х_ij = 0 означает, что задание j не назначено на машину i, а присваивание х_ijсообщает о том, что вся нагрузка t_j задания j = t_j распределена на машину i. При этом х может рассматриваться как один вектор с mn координатами.

Для кодирования требования о том, что каждое задание должно быть назначено на машину, мы воспользуемся линейными неравенствами: для каждого задания j должно выполняться условие ∑_ix_ij = t_j. Тогда нагрузка на машину i выражается в виде L_i = ∑_jx_ij. Требуется, чтобы х_ij = 0 при всех i ∉ M_j. Мы воспользуемся целевой функцией для кодирования цели — нахождения распределения, минимизирующего максимальную нагрузку. При этом нам понадобится еще одна переменная L, соответствующая нагрузке. Для всех машин i будут использоваться ∑_jx_ij < L. В итоге мы приходим к следующей формулировке задачи:

Сначала мы докажем утверждение о том, что действительные распределения однозначно соответствуют решениям х, удовлетворяющим приведенным выше ограничениям, и в оптимальном решении (GL.IP) L определяет нагрузку соответствующего присваивания.

(11.26) Распределение заданий между машинами имеет нагрузку не более L в том, и только в том случае, если вектор х, элементы которого равны х_ij = t_j для задания j, назначенного на машину i, и х_ij = 0 в противном случае, удовлетворяет ограничениям (GL.IP), где L назначает максимальную нагрузку распределения.

Рассмотрим соответствующую задачу линейного программирования, полученную заменой требования х_ij ∈ {0, t_j} более слабым требованием х_ij ≥ 0 для всех j ∈ J и i ∈ M_j. Обозначим полученную задачу линейного программирования (GL.LP). Также будет естественно добавить х_ij ≤ t_j. Мы не добавляем эти неравенства явно, так как они следуют из неотрицательности и уравнения ∑_jx_ij < = t_j, которое должно выполняться для каждого задания j.

Сразу же видно, что если существует распределение с нагрузкой не более L, то у (GL.IP) должно существовать решение со значением не более L. И наоборот:

(11.27) Если оптимальное значение (GL.LP) равно L, то оптимальная нагрузка не менее L* ≥ L.

Мы можем использовать линейное программирование для получения такого решения (х, L) за полиномиальное время. Нашей целью будет использование х для создания распределения. Вспомните, что обобщенная задача распределения нагрузки является ЖР-сложной, а следовательно, мы не можем надеяться найти ее решение в точности за полиномиальное время. Вместо этого мы найдем распределение с нагрузкой, превышающей минимум не более чем вдвое. Для этого нам также понадобится простая нижняя граница (11.2), которая уже использовалась в исходной задаче распределения нагрузки.

(11.28) Оптимальная нагрузка не меньше L* ≥ max_jt_j.

Округление решения при отсутствии циклов

Основная идея заключается в округлении значений х_ij до 0 или t_j. Однако мы не можем просто округлять большие значения в сторону увеличения, а меньшие — в сторону уменьшения. Проблема в том, что решение задачи линейного программирования может назначить малые доли задания j на каждую из m машин, а следовательно, для некоторых заданий больших значений х_ij может не быть.

Наш алгоритм будет производить “слабое” округление х: каждое задание j будет назначаться на машину i с х_ij > 0, но возможно, некоторые малые значения придется округлять в большую сторону. Слабое округление уже гарантирует, что распределение является действительным в том смысле, что никакое задание j не назначается на машину i, не входящую в M_j (потому что если i ∉ M_j, то х_ij = 0).

Важно понять структуру нецелочисленного решения и показать, что хотя некоторые задания могут быть распределены по нескольким машинам, таких заданий не может быть слишком много. Для этого мы рассмотрим следующий двудольный граф G(x) = (V(x), E(x)): множество узлов V(x) = M U J, множество заданий и множество машин и ребро (i, j) ∈ E(x) существуют в том, и только в том случае, если х_ij > 0.

Мы покажем, что при наличии решения для (GL.LP) можно получить новое решение x с такой же нагрузкой L, в котором G(x) не содержит циклов. Этот шаг очень важен, так как вы увидите, что решение x без циклов может использоваться для получения распределения с нагрузкой не более L + L*.

(11.29) Для решения (x, L) задачи (GL.LP), в котором граф G(x) не имеет циклов, решение x может использоваться для получения действительного распределения заданий между машинами с нагрузкой не более L + L* за время O(mn).

Доказательство. Так как граф G(x) не содержит циклов, каждая из его компонент связности является деревом. Распределение можно получить, рассматривая каждую компоненту по отдельности. Возьмем одну из компонент, которая представляет собой дерево; ее узлы соответствуют заданиям и машинам, как показано на рис. 11.11.

Разместим корень дерева в произвольном узле и рассмотрим задание j. Если узел, соответствующий заданию j, является узлом дерева, пусть узел машины i является его родителем. Так как степень j в дереве G(x) равна 1, машина i — единственная машина, которой была назначена часть задания j, а следовательно, должно выполняться х_ij = t_j. В нашем распределении такое задание j будет назначено только на его соседнюю машину i. Задание j, узел которого не является листовым в G(x), назначается произвольному дочернему узлу соответствующего дочернего узла в корневом дереве.

Очевидно, что этот метод может быть реализован за время O(mn) (включая время создания графа G(x)). Он определяет действительное распределение, так как задача линейного программирования (GL.LP) требует х_ij = 0 для i ∉ M_j. Чтобы завершить доказательство, необходимо показать, что нагрузка не превышает L + L*. Пусть i —любая машина, а J_i — множество заданий, назначенных на машину i. Задания, назначенные на машину i, образуют подмножество соседей i в G(x): множество J_i содержит дочерние узлы узла i, которые являются листьями, а также, возможно, родителя p(i) узла i. Чтобы ограничить нагрузку, мы рассмотрим родителя p(i) отдельно. Для всех остальных заданий j = p(i), назначенных i, x_ij = t_j, а следовательно для ограничения нагрузки можно воспользоваться решением x:

с использованием неравенства, ограничивающего нагрузку в (GL.LP). Для родителя j = p(i) узла i используется t_j ≤ L* согласно (11.28). Суммируя два неравенства, приходим к как и утверждалось. ■

Рис. 11.11. Пример графа G(x), не содержащего циклов; квадраты изображают машины, а круги — задания. Сплошными линиями обозначено итоговое распределение заданий между машинами

Теперь из (11.27) известно, что L ≤ L*, так что решение, нагрузка которого ограничивается L + L* также ограничивается 2L* — то есть удвоенный оптимум. Итак, приходим к следующему следствию из (11.29).

(11.30) Для решения (x, L) задачи (GL.LP), в котором граф G(x) не имеет циклов, решение x может использоваться для получения действительного распределения заданий между машинами с нагрузкой, не превышающей удвоенного оптимума, за время O(mn).

Исключение циклов из решения задачи линейного программирования

Чтобы завершить аппроксимирующий алгоритм, остается лишь показать, как преобразовать произвольное решение (GL.LP) в решение x, не содержащее циклов в G(x). Попутно мы также покажем, как получить решение задачи линейного программирования (GL.LP) с использованием потоковых вычислений. А точнее, для заданного значения нагрузки L мы покажем, как при помощи потоковых вычислений решить, имеет ли (GL.LP) решение со значением не более L. Для этого рассмотрим направленный граф G = (V, E), изображенный на рис. 11.12. Множество вершин потокового графа G V = M U J U {v}, где v — новый узел. Узлы j ∈ J будут источниками с поставкой t_j, а единственным потребляющим узлом будет новый сток v с уровнем потребления ∑_jt_j. Поток в этой сети будет рассматриваться как “перетекание” нагрузки из заданий в сток v через машины. Ребро (j, i) с бесконечной пропускной способностью от задания j к машине iдобавляется в том, и только в том случае, если i ∈ M_j. Наконец, мы добавляем ребро (i, v) для каждого узла машины i с пропускной способностью L.

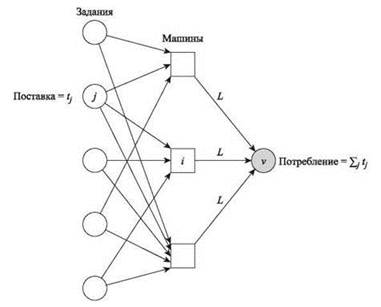
Рис. 11.12. Схема вычисления потока в сети, используемая для поиска решения (GL.LP). Ребра между заданиями и машинами обладают бесконечной пропускной способностью

(11.31) Решения задачи нахождения потока с пропускной способностью L однозначно соответствуют решениям (GL.LP) со значением L, где х_ij — величина потока по ребру (i, j), а величина потока по ребру (i, t) равна нагрузке ∑_jt_j на машине i.

Это утверждение позволяет решить (GL.LP) с использованием потоковых вычислений и бинарного поиска для оптимального значения L: мы последовательно опробуем значения L, пока не найдем минимальное, для которого существует действительный поток.

Воспользуемся информацией, полученной о (GL.LP) из эквивалентной формулировки задачи нахождения потока, и изменим решение х для устранения из G(x) всех циклов. В контексте только что определенного потока G(x) представляет собой ненаправленный граф, для получения которого в G игнорируются направления ребер, удаляется сток v и все прилегающие ребра, а также удаляются все ребра из J в M, по которым не передается поток. Удаление всех циклов из G(x) будет выполнено не более чем за mn шагов, а целью каждого шага является исключение из G(x) по крайней мере одного ребра без увеличения нагрузки L или добавления новых ребер.

(11.32) Пусть (x, L) — произвольное решение (GL.LP), а C — цикл в G(x). За время, линейное по отношению к длине цикла, можно изменить решение x для исключения из G(x) по крайней мере одного ребра без увеличения нагрузки или добавления новых ребер.

Доказательство. Рассмотрим цикл C в G(x). Вспомните, что G(x) соответствует множеству ребер, передающих поток в решении x. Мы изменим решение, увеличивая поток по циклу C; для этого будет использоваться процедура augment из раздела 7.1. Увеличение потока в цикле не изменит баланс между входным и выходным потоком в любом узле; вместо этого оно приведет к исключению одного обратного ребра из остаточного графа, а следовательно, ребра из G(x). Предположим, узлы в цикле обозначаются i₁, j₁, i₂, j₂, ..., i_k, j_k, где i_l — узел машины, а j_l — узел задания. Мы изменим решение, сокращая поток по всем ребрам (i_l, j_l) и увеличивая поток по ребрам (j_l, i_l+1) для всех l = 1, ..., k (где k + 1 обозначает 1) на одинаковую величину δ. Изменение не повлияет на ограничения сохранения потока. Задавая мы гарантируем, что поток остается действительным, а ребро, в котором достигается минимум, удаляется из G(x). ■

Алгоритм, содержащийся в доказательстве (11.32), можно применить многократно для удаления всех циклов из G(x). В исходном состоянии G(x) может содержать mn ребер, так что после максимум O(mn) итераций полученное решение (x, L) не содержит циклов в G(x). На этой стадии можно применить (11.30) для получения действительного распределения с нагрузкой, превышающей оптимум не более чем вдвое.

(11.33) Для заданного экземпляра обобщенной задачи распределения нагрузки может быть найдено за полиномиальное время действительное распределение с нагрузкой, превышающей возможный минимум не более чем вдвое.