Упражнения с решениями - Урок 11 - Аппроксимирующие алгоритмы

Упражнение с решением 1

Вспомните жадный алгоритм для задачи интервального планирования: для заданного множества интервалов многократно выбирается кратчайший интервал I, удаляются все остальные интервалы I', пересекающиеся с I, после чего все повторяется.

В главе 4 было показано, что алгоритм не всегда строит множество максимального размера с неперекрывающимися интервалами. Однако, как выясняется, он предоставляет интересную гарантию аппроксимации. Если s* — максимальный размер множества неперекрывающихся интервалов, а s — размер множества, произведенного этим алгоритмом, то s ≥ 1/2s* (то есть алгоритм выбора кратчайшего интервала является 2-аппроксимацией).

Докажите этот факт.

Решение

Вспомним пример на рис. 4.1 из главы 4: он показывал, что алгоритм выбора кратчайшего интервала не обязательно находит оптимальное множество интервалов. Проблема очевидна: выбор короткого интервала j может привести к исключению двух более длинных прилегающих интервалов i и i', так что алгоритм наполовину уступает оптимуму.

Вопрос в том, как показать, что алгоритм выбора кратчайшего интервала никогда не работает хуже этого. Возникающие проблемы напоминают те, которые встречались в ходе анализа жадного алгоритма для задачи максимальных непересекающихся путей из раздела 11.5: каждый выбираемый интервал может “блокировать” некоторые интервалы в оптимальном решении, и мы хотим обосновать, что при постоянном выборе кратчайшего возможного интервала последствия от блокировки будут умеренными. В случае непересекающихся путей перекрытия между путями приходилось анализировать ребро за ребром, так как используемый граф мог иметь произвольную структуру. На этот раз можно воспользоваться сильно ограниченной структурой интервалов на линии для получения усиленной границы.

Чтобы алгоритм выбора кратчайшего интервала работал хуже, чем наполовину от оптимума, должно существовать большое оптимальное решение, которое перекрывается с много меньшим решением, выбираемым алгоритмом. Интуитивно кажется, что единственная ситуация, в которой это может произойти, — если один из интервалов i в оптимальном решении полностью укладывается в один из интервалов j, выбираемых алгоритмом выбора кратчайшего пути. Однако это противоречит поведению алгоритма: почему он не выбрал более короткий интервал i, вложенный в j?

Посмотрим, удастся ли точно сформулировать этот аргумент. Пусть A — множество интервалов, выбираемых алгоритмом, а O — оптимальное множество интервалов. Для каждого интервала j ∈ Aрассмотрим множество интервалов в O, с которыми он конфликтует.

(11.41) Каждый интервал j ∈ A конфликтует не более чем с двумя интервалами в O.

Доказательство. Действуя от обратного, предположим, что в j ∈ A существует интервал, конфликтующий не менее чем с тремя интервалами из i₁, i₂, i₃ ∈ O. Эти три интервала не конфликтуют друг с другом, так как они являются частью одного решения O, поэтому они располагаются последовательно во времени. Предположим, сначала идет i₁, затем i₂, а потом i₃. Так как интервал jконфликтует и с i₁ и с i₃, расположенный между ними интервал i₂ должен быть короче j и полностью помещаться в нем. Кроме того, так как интервал i₂ не был выбран алгоритмом, он должен был быть доступен как вариант на тот момент, когда алгоритм выбрал интервал j. Возникает противоречие, так как i₂ короче j. ■

Алгоритм выбора кратчайшего пути завершается только тогда, когда каждый невыбранный интервал конфликтует с одним из выбранных интервалов. Следовательно, каждый интервал в O либо включается в A, либо конфликтует с интервалом в A.

Теперь мы воспользуемся следующей схемой для ограничения количества интервалов в O. Для каждого i ∈ O некоторый интервал j ∈ A “платит” за i следующим образом: если i также принадлежит A, то i платит за себя. В противном случае мы произвольно выбираем интервал j ∈ A, конфликтующий с i. Как было показано выше, каждый интервал в O конфликтует с некоторым интервалом в A, так что все интервалы в O будут оплачиваться по этой схеме. Однако согласно (11.41), каждый интервал j ∈ A конфликтует не более чем с двумя интервалами в O, поэтому он заплатит не более чем за два интервала. Следовательно, все интервалы в O оплачены интервалами в A, и в этом процессе каждый интервал в A платит максимум два раза. Из этого следует, что множество A должно содержать не менее половины от количества интервалов O.

Упражнения

1. Предположим, вы консультируете управление порта в маленькой стране на побережье Тихого океана. Ежегодный объем сделок исчисляется миллиардами, и доход ограничивается исключительно скоростью разгрузки кораблей, прибывающих в порт.

Типичная задача, возникающая в работе порта, выглядит так: прибывает корабль с n контейнерами веса w₁, w₂, ..., w_n. В доке стоят грузовики, каждый из которых способен перевозить до Kединиц веса. (Считайте, что K и все w_i являются целыми числами.) В один грузовик можно погрузить несколько контейнеров, на которые распространяется ограничение по весу K; целью является минимизация количества грузовиков, необходимых для перевозки всех контейнеров. Задача является NР-полной (это доказывать не надо).

Жадный алгоритм для решения этой задачи мог бы выглядеть так: начать с пустого грузовика и загружать в него контейнеры 1, 2, 3 ... до тех пор, пока вы не доберетесь до контейнера, который приведет к нарушению ограничения. Этот грузовик объявляется “загруженным” и отправляется, после чего процесс повторяется со следующим грузовиком. Алгоритм, рассматривающий грузовики по отдельности, может не обеспечить самый эффективный способ упаковки всего множества контейнеров в доступное множество грузовиков.

(a) Приведите пример множества весов и значения K, при которых алгоритм не использует минимально возможное количество грузовиков.

(b) Покажите, что количество грузовиков, используемых этим алгоритмом, не более чем в 2 раза превышает минимально возможное для любого множества весов и любого значения K.

2. На лекции по вычислительной биологии, которую один из авторов посетил несколько лет назад, известный химик рассказывал об идее построения “представительного множества” для обширного множества белковых молекул, свойства которых нам непонятны. Идея заключается в том, чтобы интенсивно изучать белки из представительного множества и тем самым получить информацию (косвенно) обо всех белках полного множества.

Чтобы представительное множество приносило пользу, оно должно обладать двумя свойствами:

• оно должно быть относительно небольшим, чтобы его изучение не обходилось слишком дорого;

• каждый белок в полном множестве должен быть “похож” на некоторый белок из представительного множества. (То есть множество действительно предоставляет некоторую информацию обо всех белках.)

В более конкретной формулировке существует большое множество белков P. Сходство между белками определяется функцией расстояния d: для двух белков p и q эта функция возвращает число d(p, q) ≥ 0. Функция d(∙,∙) обычно используется в качестве метрики выравнивания последовательностей (эта задача рассматривалась при изучении динамического программирования в главе 6); будем считать, что она используется и в этом случае. Существует заранее определенный порог расстояния Δ, который задается как часть входных данных задачи; два белка p и qсчитаются “похожими” в том, и только в том случае, если d(p, q) ≤ Δ. Подмножество P называется представительным множеством, если для каждого белка p существует похожий на него белок q, принадлежащий этому подмножеству, то есть белок, для которого d(p,q) ≤ Δ. Требуется найти представительное множество минимального размера.

(a) Предложите алгоритм с полиномиальным временем, аппроксимирующий минимальное представительное множество до множителя O(log n). В более конкретной формулировке алгоритм должен обладать следующим свойством: если минимальный возможный размер представительного множества равен s*, то алгоритм должен возвращать представительное множество с размером не более O(s* log n).

(b) Обратите внимание на сходство этой задачи с задачей о выборе центров; аппроксимирующие алгоритмы для последней рассматривались в разделе 11.2. Почему описанный там алгоритм не решает текущую задачу?

3. Допустим, имеется множество положительных целых чисел A = {a₁, a₂, ..., a_n} и положительное целое число B. Подмножество S ⊆ A будет называться действительным, если сумма чисел в Sне превышает B:

Сумма чисел в S называется полной суммойS.

Требуется выбрать действительное подмножество S множестваA с максимально возможной полной суммой.

Пример. Если A = {8,2,4} и B = 11, то оптимальным решением будет подмножество S = {8,2}.

(a) Рассмотрим следующий алгоритм для решения этой задачи.

Приведите пример, в котором полная сумма множества S, возвращаемого этим алгоритмом, меньше половины полной суммы некоторого действительного подмножества A.

(b) Предложите аппроксимирующий алгоритм с полиномиальным временем, предоставляющий следующую гарантию: полная сумма возвращаемого действительного множества S ⊆ A не меньше половины максимальной полной суммы любого действительного множества S' ⊆ A. Время выполнения алгоритма не должно превышать O(n log n).

4. Рассмотрим оптимизированную версию задачи о множестве представителей, которая определяется следующим образом. Имеется множество A = {a₁, ..., a_n} и набор B₁, B₂, ..., B_mподмножеств A. Кроме того, каждый элемент a_i ∈ A имеет вес w_i ≥ 0. Требуется найти множество представителей Н ⊆ А с минимально возможным общим весом элементов Н — то есть (Как и в упражнении 5 главы 8, множеством представителей называется такое множество H, что H ∩ B_i не пусто для всех i.) Обозначим b = max_i|B_i| максимальный размер множеств B₁, B₂, ..., B_m. Предложите аппроксимирующий алгоритм с полиномиальным временем для нахождения множества представителей, общий вес которого не более чем в b раз превышает минимально возможный.

5. Вы работаете на фирму, клиенты которой ежедневно предоставляют задания для обработки. Каждое задание характеризуется временем обработки t, известным при поступлении задания. Компания располагает парком из 10 машин, и каждое задание может быть выполнено на любой машине.

В настоящее время фирма использует простой жадный алгоритм распределения нагрузки, рассмотренный в разделе 11.1. Директор фирмы знает, что этот аппроксимирующий алгоритм может быть не лучшим, и интересуется, нужно ли опасаться неэффективности. Впрочем, изменять механизм он не хочет, потому что ему нравится простота текущего алгоритма: задания можно назначать машинам сразу же после поступления, не откладывая принятие решения до прихода новых заданий.

В частности, он слышал, что этот алгоритм может строить решения с периодом обработки вдвое больше минимума. Однако в целом опыт использования алгоритма был вполне неплох: он ежедневно выполнялся в течение последнего месяца, и период обработки ни разу не превысил среднюю нагрузку 1/10∑_it_i более чем на 20 %.

Чтобы понять, почему “удвоенное” поведение не проявляется в работе, вы собираете информацию о типичных заданиях и нагрузках. Как выясняется, размеры заданий лежат в диапазоне от 1 до 50, то есть 1 ≤ t_i ≤ 50 для всех заданий i; а ежедневная общая нагрузка ∑_it_i, достаточно высока: она не бывает ниже 3000.

Докажите, что для таких входных данных жадный алгоритм распределения нагрузки всегда находит решение, продолжительность обработки которого превышает среднюю не более чем на 20 %.

6. Вспомните, что в базовой задаче распределения нагрузки из раздела 11.1 нас интересовало распределение заданий между машинами, минимизирующее период обработки — максимальную нагрузку на одной машине. Достаточно часто приходится рассматривать случаи, в которых доступны машины с разной вычислительной мощью, так что конкретное задание может завершиться на одной из машин быстрее, чем на другой. Вопрос: как распределять задания между машинами в разнородной системе?

Все эти проблемы продемонстрированы в следующей базовой модели. Допустим, имеется система, состоящая из m медленных и k быстрых машин. Быстрые машины могут выполнять за единицу времени вдвое больше работы, чем медленные. Имеется множество из n заданий; выполнение задания i занимает время t_i на медленной машине и время 1/2t_i на быстрой машине.

Требуется назначить каждое задание на машину; как и прежде, целью является минимизация периода обработки, то есть максимума (по всем машинам) общего времени обработки заданий, назначенных на каждую машину.

7. Предложите алгоритм с полиномиальным временем, который обеспечивает распределение заданий между машинами с периодом обработки, превышающим оптимум не более чем в три раза.

Вы консультируете коммерческий сайт, который ежедневно получает большое количество посещений. Каждому посетителю i, где i ∈ {1, 2, ..., n}, сайт назначает значение v_i, представляющее ожидаемый доход, который может быть получен о данного клиента.

Каждому посетителю i при входе на сайт показывается одна из m возможных реклам A₁, A₂, ..., A_m. Нужно выбрать по одной рекламе для каждого посетителя, чтобы каждая реклама была показана в сумме множеству клиентов с достаточно большим общим весом. Таким образом, для заданного выбора одной рекламы на посетителя охват этой выборки определяется как минимум по 1, 2, ..., m общего веса всех клиентов, которым была показана реклама A_j.

Пример. Допустим, имеются шесть посетителей со значениями 3, 4, 12, 2, 4, 6 и m = 3 реклам. Тогда в этом экземпляре задачи можно обеспечить охват 9, показав рекламу A₁ посетителям 1, 2, 4, рекламу A₂ — посетителю 3 и рекламу A₃ — посетителям 5 и 6.

Конечной целью является подбор рекламы для каждого посетителя, обеспечивающей максимальный охват. К сожалению, задача оптимизации является NP-сложной (вам это доказывать не нужно). Итак, вместо поиска прямого решения мы попробуем аппроксимировать его.

(a) Предоставьте алгоритм с полиномиальным временем, аппроксимирующий максимальный охват в пределах множителя 2. Иначе говоря, если максимальный охват равен s, то ваш алгоритм должен выдавать подборку рекламы с охватом не менее s/2. При разработке алгоритма можно считать, что в ней нет посетителей, значение которых значительно превышает среднее; а именно: если обозначить общее значение по всем посетителям, можно считать, что нет посетителя со значением, превышающим

(b) Приведите пример экземпляра, для которого алгоритм, разработанный в части (а), не находит оптимального решения (то есть решения с максимальным охватом). Укажите в своем примере оптимальное решение и решение, которое будет найдено вашим алгоритмом.

8. Ваши друзья работают над системой, выполняющей планирование заданий на нескольких серверах в реальном времени. Они обратились к вам за помощью — им нужно как-то справиться с неэффективным кодом, который не может быть изменен.

Ситуация выглядит так: при поступлении пакета заданий система распределяет их по серверам, используя простой жадный алгоритм распределения из раздела 11.1, обеспечивающий аппроксимацию в пределах множителя 2. Однако эта часть системы была написана уже 15 лет назад, а производительность оборудования возросла до такого уровня, что в экземплярах задачи, с которыми имеет дело система, обычно бывает возможно вычислить оптимальное решение. Проблема в том, что люди, отвечающие за администрирование системы, не позволяют изменить часть кода, реализующую жадный алгоритм распределения нагрузки, и заменить его кодом поиска оптимального решения. (Эта часть кода взаимодействует с множеством других модулей системы, поэтому риск возникновения проблем в случае замены слишком велик.)

Немного поворчав, ваши друзья выдвигают альтернативную идею. Допустим, они могут написать маленький фрагмент кода, который получает описание заданий, вычисляет оптимальное решение (так как они могут сделать это с экземплярами, встречающимися на практике), а потом передает задания жадному алгоритму в таком порядке, который заставит его расположить их оптимальным образом. Иначе говоря, они надеются переупорядочить входные данные так, чтобы при получении данных в новом порядке жадный алгоритм выдавал оптимальное решение.

Ваших друзей интересует: всегда ли это возможно? Они предлагают следующую гипотезу.

Для каждого экземпляра задачи распределения нагрузки из раздела 11.1 существует такой порядок заданий, что при обработке заданий в этом порядке жадный алгоритм распределения нагрузки строит распределение с минимально возможным периодом обработки.

Решите, истинна ли эта гипотеза или ложна; приведите доказательство или контрпример.

9. Рассмотрим следующую максимизирующую версию задачи о трехмерном сочетании. Для заданных непересекающихся множеств X, Y и Z, а также множества T ⊆ X х Y х Z упорядоченных триплетов подмножество M ⊆ T называется трехмерным сочетанием, если каждый элемент X U Y U Z содержится не более чем в одном из этих триплетов. В максимальной задаче о трехмерном сочетании требуется найти трехмерное сочетание M с максимальным размером. (Размер сочетания, как обычно, определяется количеством содержащихся в нем триплетов. Если хотите, считайте, что |X| = |Y| = |Z|.)

Предложите алгоритм с полиномиальным временем, который находит трехмерное сочетание с размером не менее 1/3 от максимально возможного.

10. Предположим, имеется решетчатый граф G с размерами n х n (рис. 11.13).

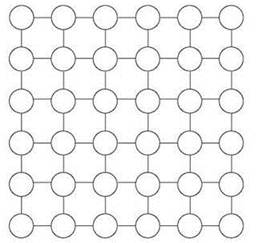
Рис. 11.13. Решетчатый граф

С каждым узлом v связывается вес w(v) — неотрицательное целое число. Считайте, что веса всех узлов различны. Требуется найти такое независимое множество S узлов решетки, чтобы сумма весов узлов S была как можно выше. (Далее сумма весов узлов множества S будет называться его общим весом.)

Рассмотрим следующий жадный алгоритм для решения этой задачи.

(a) Пусть S — независимое множество, возвращаемое жадным алгоритмом выбора узла с наибольшим весом, а T — любое независимое множество в G. Покажите, что для каждого узла v ∈ Tлибо v ∈ S, либо существует такой узел v' ∈ S, что w(v) ≤ w(v) и (v, v') является ребром G.

(b) Покажите, что жадный алгоритм выбора узла с наибольшим весом возвращает независимое множество с общим весом не менее 1/4 от максимального общего веса любого независимого множества в решетчатом графе G.

11. Вспомните, что в задаче о рюкзаке имеются n предметов, каждый из которых обладает весом w_i и значением v_i. Также определяется предельный вес W; задача состоит в нахождении множества предметов S с наибольшим возможным значением при условии, что общий вес не превышает W, то есть Один из подходов к рассмотрению аппроксимирующих алгоритмов может быть таким: если существует подмножество О, общий вес которого равен а общее значение для некоторого V, то наш аппроксимирующий алгоритм найдет множество А с общим весом и общим значением не менее Таким образом, алгоритм аппроксимирует лучшее значение, удерживая веса строго ниже W. (Конечно, возвращение множества O всегда является действительным решением, но так как задача является NР-полной, не стоит рассчитывать, что нам всегда удастся найти само множество O; граница аппроксимации 1 + є означает, что другие множестваA, обладающие чуть меньшим значением, также могут быть действительными ответами.)

Но всем известно, что в чемодан всегда можно добавить еще немного вещей, если посидеть на нем, — другими словами, если слегка превысить допустимый предельный вес. Отсюда тоже вытекает способ формализации вопроса об аппроксимации задачи о рюкзаке, но это уже другая формализация.

Допустим, как и прежде, даны n предметов с весами и значениями, а также параметрами W и V; вам сообщают, что существует подмножество О, общий вес которого равен а общее значение равно для некоторого V. Для заданного фиксированного є > 0 разработайте алгоритм с полиномиальным временем, который находит подмножество таких элементов А, что И

Другими словами, подмножество A должно достигать общего значения, не меньшего заданной границы V, но допускается превышение границы веса W на коэффициент 1 + є.

Пример. Допустим, имеются четыре предмета со следующими весами и значениями:

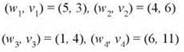
Также заданы границы W = 10 и V = 13 (так как подмножество, состоящее из первых трех элементов, имеет общий вес 10 и значение 13). Наконец, є = 0,1. Это означает, что нужно найти (при помощи аппроксимирующего алгоритма) подмножество с весом не более (1 + 0,1) * 10 = 11 и значением не менее 13. Одним из действительных решений станет подмножество, состоящее из первого и четвертого предметов, со значением 14 ≥ 13. (Обратите внимание: в этом случае достигается значение строго большее V, так как допускается легкое переполнение рюкзака.)

12. Рассмотрим следующую задачу. Имеется множество U из n узлов, которые могут рассматриваться как пользователи (например, пользователи, обращающиеся к веб-серверу или иному виду сервиса). Серверы должны размещаться в разных местах. Предположим, имеется множество из S возможных мест, подходящих для размещения серверов. Для каждого места s ∈ S определяется плата за размещение установки сервера в этом месте f_s ≥ 0. Ваша цель — обеспечить аппроксимированную минимизацию стоимости при предоставлении сервиса каждому пользователю. Пока что все очень похоже на задачу о покрытии множества: места s соответствуют множествам, вес множества s равен f_s, требуется выбрать совокупность множеств, покрывающую всех пользователей. Тем не менее существует один нюанс: пользователи u ∈ U могут обслуживаться из разных мест, но за обслуживание пользователя u из места s взимается стоимость d_us. При очень высоком значении d_us обслуживание пользователя и с сервера в месте s нежелательно; в общем случае затраты d_us должны поощрять обслуживание пользователей с “ближних” серверов, насколько это возможно. Итак, вопрос, который мы назовем “задачей о размещении серверов”: для заданных множеств U и S, а также цен f и d требуется выбрать подмножество мест А ⊆ S для размещения серверов (со стоимостью ) и закрепить за каждым пользователем активный сервер, на котором его обслуживание обойдется дешевле всего: Целью является минимизация общих затрат Предложите H(n)-аппроксимацию для этой задачи. (Если все значения d_us равны 0 или бесконечны, то задача в точности соответствует задаче покрытия множеств: f_s — стоимость множества s, а d_us = 0, если узел u принадлежит множеству s, и бесконечность в противном случае).

Примечания и дополнительная литература

В области разработки аппроксимирующих алгоритмов для NР-сложных задач ведутся активные исследования; в частности, этой теме посвящен сборник статей под редакцией Хохбаума (Hochbaum, 1996) и работа Вазирани (Vazirani, 2001).

Автором жадного алгоритма распределения нагрузки и его анализа стал Грэм (Graham, 1966, 1969); в частности, он доказал, что когда задания предварительно сортируются в порядке убывания размера, жадный алгоритм обеспечивает распределение в границах коэффициента 4/3 от оптимума. (В тексте приводится более простое доказательство ослабленной границы 3/2).

При использовании более сложных алгоритмов для этой задачи доказываются даже более сильные гарантии аппроксимации (Hochbaum, Shmoys, 1987; Hall, 1996). Методы, используемые усиленными аппроксимирующими алгоритмами распределения нагрузки, также тесно связаны с методом, описанным в тексте при разработке аппроксимаций произвольной точности для задачи о рюкзаке.

Аппроксимирующий алгоритм для задачи о выборе центров следует методологии Хохбаума и Шмойса (Hochbaum, Shmoys, 1985), а также Дайера и Фризе (Dyer, Frieze, 1985). Другие геометрические задачи выбора мест этого типа обсуждаются Берном и Эппстейном (Bern, Eppstein, 1996), а также в сборнике под редакцией Дрезнера (Drezner, 1995).

Жадный алгоритм для задачи покрытия множества и ее анализ были выполнены независимо Джонсоном (Johnson, 1974), Ловашем (Lovasz, 1975) и Хваталом (Chvatal, 1979). Дальнейшие результаты для задачи покрытия множества обсуждаются в сборнике Хохбаума (Hochbaum, 1996).

Как упоминалось в тексте, метод назначения цены при разработке аппроксимирующих алгоритмов также называется прямо-двойственным методом и может быть обоснован средствами линейного программирования. Последний метод является темой работы Геманса и Уильямсона (Goemans, Williamson, 1996). Алгоритм назначения цены для аппроксимации взвешенной задачи о вершинном покрытии предложили Бар-Иегуда и Ивен (Bar-Yehuda, Even, 1981). Жадный алгоритм для задачи о непересекающихся путях разработан Клейнбергом и Тардос (Kleinberg, Tardos, 1995); аппроксимирующий алгоритм на базе цен для случая с повторным использованием ребер несколькими путями предложили Авербух, Азар и Плоткин (Awerbuch, Azar, Plotkin, 1993). Алгоритмы были разработаны и для многих других разновидностей задачи о непересекающихся путях; в сборнике под редакцией Корте и др. (Korte, 1990) обсуждаются случаи, имеющие оптимальное решение за полиномиальное время, а у Плоткина (Plotkin, 1995) и Клейнберга (Kleinberg, 1996) приводится анализ текущих работ по аппроксимации.

Округляющий алгоритм линейного программирования для взвешенной задачи о вершинной покрытии предложен Хохбаумом (Hochbaum, 1982). Округляющий алгоритм для обобщенной задачи распределения нагрузки разработали Ленстра, Шмойс и Тардос (Lenstra, Shmoys, Tardos, 1990); другие результаты в этом направлении представлены в обзоре Холла (Hall, 1996). Как упоминалось в тексте, эти два результата демонстрируют распространенный метод разработки аппроксимирующих алгоритмов: формулировка задачи в контексте целочисленного программирования, преобразование ее во взаимосвязанную (но не эквивалентную) задачу линейного программирования и последующее округление полученного решения. Многие другие применения этого метода обсуждаются у Вазирани (Vazirani, 2001).

Два других эффективных метода разработки аппроксимирующих алгоритмов — локальный поиск и рандомизация; эти связи обсуждаются в следующих двух главах.

В книге не затронута тема неаппроксимируемости. По аналогии с тем, как можно доказать, что заданная NP-сложная задача может быть аппроксимирована до некоторого множителя за полиномиальное время, также иногда удается установить нижние границы, которые показывают, что если задача может быть аппроксимирована лучше, чем до некоторого множителя c за полиномиальное время, то она может быть решена оптимально; тем самым будет доказано, что Р = NP. В этой области проводится растущее число исследований, устанавливающих пределы аппроксимируемости для многих NP-сложных задач. В некоторых случаях эти положительные и отрицательные результаты идеально сочетаются и образуют порог аппроксимации, устанавливая для некоторых задач наличие аппроксимирующего алгоритма до множителя c с полиномиальным временем и невозможность более эффективного решения при условии Р ≠ NP. Некоторые ранние результаты в области неаппроксимируемости доказывались без особых трудностей, но в последних работах появились мощные и весьма нетривиальные методы. Эта тема рассматривается в работе Ароры и Лунда (Arora, Lund, 1996).

Примечания к упражнениям

Упражнения 4 и 12 основаны на результатах Дорита Хохбаума. Упражнение 8 основано на результатах Сартаджа Сани, Оскара Ибарры и Чул Кима, а также Дорита Хохбаума и Дэвида Шмойса.

---

¹ Один ученый, работающий в области телекоммуникаций, однажды так объяснил различия между задачами максимальных непересекающихся путей и потока в сети и суть нарушения сведения из предыдущего абзаца. В День матери, когда количество звонков традиционно достигает максимума, телефонной компании приходится решать грандиозную задачу непересекающихся путей: следить за тем, чтобы каждый источник s_i был связан путем по голосовой сети со своей матерью t_i. С другой стороны, алгоритмы сетевого потока, ищущие непересекающиеся пути между множеством S и множеством T, обещают лишь то, что каждый человек дозвонится до чьей-то матери.

² Читатели, знакомые со свойством двойственности, могут также заметить, что метод назначения цены из предыдущего раздела также работает на основе двойственности линейного программирования: цены точно соответствуют переменным в двойственной задаче линейного программирования (и это объясняет, почему алгоритмы назначения цены часто называются прямо-двойственными алгоритмами).