Числовые исполнители - Элементы теории алгоритмов

Конспект

Исполнитель — субъект (человек, животное) или устройство, способное выполнить действия, предписываемые алгоритмом. При этом указанные действия выполняются формально. Исполнитель не знает о цели алгоритма, он лишь выполняет все полученные команды.

Каждый исполнитель характеризуется следующими параметрами:

— среда — условия, в которых функционирует исполнитель (например, исполнитель Черепашка имеет определенную систему координат, исполнитель Робот перемещается по клетчатому полю и т.д.);

— система команд — каждый исполнитель может выполнять команды только из некоторого строго заданного набора, где каждая команда определяет соответствующее элементарное действие.

Алгоритм — запись в той или иной форме (словесной, графической, на языке программирования) последовательности команд для исполнителя. Команды алгоритма должны соответствовать системе команд исполнителя.

Алгоритмические конструкции

1. Следование — последовательное выполнение команд сверху вниз (линейный алгоритм).

2. Ветвление — команды выполняются в зависимости от истинности некоторого условия либо возможно выполнение одного из двух или более наборов команд в зависимости от истинности условия.

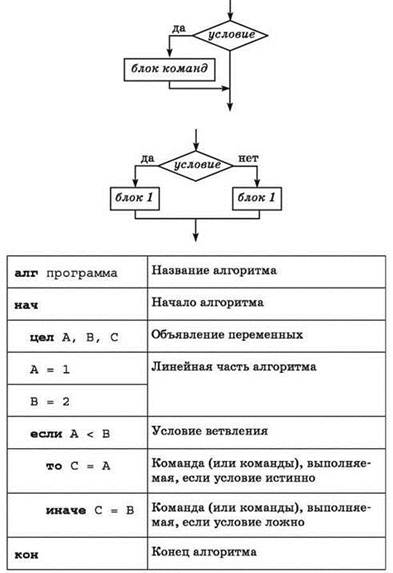
3. Цикл — многократное повторение блока команд (количество повторений зависит от условия цикла либо задаётся явно).

Цикл с предусловием

(цикл ПОКА)

Блок команд выполняется, пока условие остаётся истинным (выход из цикла — по ложности условия).

Условие проверяется до начала выполнения цикла, поэтому возможна ситуация, что тело цикла не будет выполнено ни разу.

Цикл с постусловием

(цикл ДО)

Блок команд выполняется до тех пор, пока условие не станет истинным (цикл выполняется, пока условие ложно).

Условие проверяется после выполнения цикла, поэтому тело цикла всегда выполняется хотя бы один раз.

Цикл с параметром

(цикл со счётчиком, цикл ДЛЯ)

Блок команд выполняется количество раз, заданное начальным, конечным значениями переменной-счётчика и шагом её изменения.

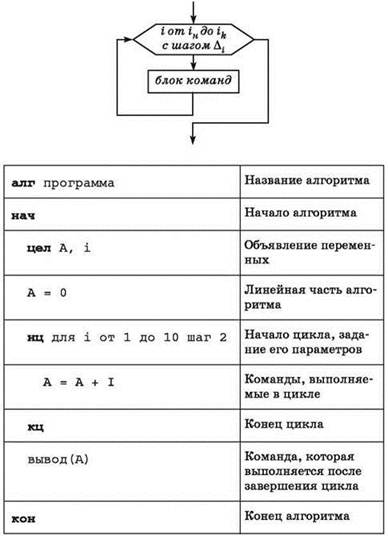
Первоначально переменной-счётчику (в данном примере — переменной i) присваивается начальное значение i_н и выполняется тело цикла. После выполнения тела цикла значение счётчика увеличивается на заданную величину шага Δi и выполняется проверка: не превысило ли значение счётчика заданное конечное значение i_к. Если не превысило, то вновь выполняется тело цикла. Иначе происходит выход из цикла.

4. Подпрограмма — поименованный блок команд выполняется после их вызова из любого места основной программы. При этом одна и та же подпрограмма может быть вызвана из основной программы любое количество раз и ей каждый раз могут передаваться свои значения переменных (параметров).

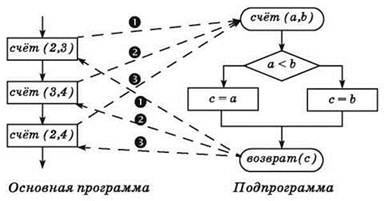
Разбор типовых задач

Задача 1. У исполнителя Калькулятор две команды, которым присвоены номера:

1. прибавь 1

2. умножь на 3

Выполняя первую из них, Калькулятор прибавляет к числу на экране 1, а выполняя вторую, утраивает его. Запишите порядок команд в программе получения из числа 2 числа 26, содержащей не более 6 команд, указывая лишь номера команд.

(Например, программа 21211 — это программа

умножь на 3

прибавь 1

умножь на 3

прибавь 1

прибавь 1

которая преобразует число 1 в 14.)

Решение

Решать такую задачу проще всего “с конца”: сначала записать число, которое надо получить (в данном случае 26), а затем пытаться от него прийти к исходному числу (2), используя “обратные” команды Исполнителя (в данном случае — вычесть 1 и разделить на 3). При этом, поскольку программа должна содержать мало команд (всего 6), надо прийти к числу 2 как можно быстрее.

Значит, надо по возможности использовать команду деления на 3, а к вычитанию прибегать, если разделить число нацело на 3 не удаётся. Итак:

Команда	Текущее число
	26
вычесть 1	25
вычесть 1	24
разделить на 3	8
вычесть 1	7
вычесть 1	6
разделить на 3	2

Остаётся записать эту программу в обратном порядке (от числа 2 к числу 26), используя изначальные команды Исполнителя — прибавить 1 и умножить на 3:

Команда	Текущее число
	2
умножить на 3	6
прибавить 1	7
прибавить 1	8
умножить на 3	24
прибавить 1	25
прибавить 1	26

Если теперь записать (как требуется в задаче) последовательность порядковых номеров этих команд, получается программа: 211211.

Ответ: 211211.

Задача 2. У исполнителя есть две команды, которые кодируются своими номерами:

1. вычесть 3

2. делить на 2

Выполняя первую из них, исполнитель вычитает из текущего числа число 3. Выполняя вторую команду, исполнитель делит текущее число пополам (но если деление нацело невозможно, то выполнение программы прекращается).

Требуется записать программу, состоящую из номеров соответствующих команд, содержащую не более 5 команд и преобразующую число 186 в число 39. При этом номера команд записываются в нужном порядке подряд, без пробелов. Если возможно несколько таких программ, то запишите любую из них.

Например, для программы:

вычесть 3

разделить на 2

вычесть 3

надо записать программу в виде: 121. Такая программа, например, преобразует число 37 в число 14.

Решение

В предыдущей задаче рекомендовалось начинать решение “с конца” — сначала заменить заданные команды на обратные им и найти программу, которая приводит от требуемого числа к исходному, — а затем записать номера “прямых” команд в обратном порядке по отношению к найденному. Но эту задачу нужно решать сразу напрямую, не заменяя команды на обратные!

Дело в том, что в предыдущих задачах команды были такими: “сложить”, “вычесть”, “умножить”, а иногда — “возвести в квадрат”. Работать с ними сложно: имея некоторое “промежуточное” число, трудно предугадать, какую команду лучше всего к нему применить, чтобы дойти до результата (разве что, зная, что программа должна быть короткой, можно догадаться, что надо стараться использовать умножение и возведение в квадрат, а не сложение, чтобы быстрее дойти до цели). А если заменить такие команды на “обратные”, то получившиеся команды деления и вычисления квадратного корня сразу становились подсказкой: если текущее число делится нацело или из него можно извлечь целый корень, то это означает, что надо использовать именно такую команду, а если деление или извлечение корня нацело не удаётся, то использовать “альтернативное” сложение или вычитание.

В данной задаче уже имеется команда деления. Значит, она станет такой же подсказкой, если мы будем решать задачу напрямую.

186	делить на 2	(число делится нацело )
93	вычесть 3	(не делится нацело на 2)
90	делить на 2	(число делится нацело )
45	вычесть 3	(не делится нацело на 2)
42	вычесть 3	(уже нетрудно догадаться, что нужно не делить на 2, а вычесть 3)
39

Остаётся записать в том же порядке номера команд.

Ответ: 21211.

Итак, прежде всего нужно смотреть на то, какие у исполнителя команды. Если среди них есть такие команды, которые могут быть выполнены только при определённых условиях (деление нацело, извлечение целого квадратного корня), то задачу надо решать “напрямую”. А если все команды такие, что могут быть выполнены всегда (сложение, умножение, вычитание, возведение в квадрат), то лучше сначала решить задачу с “обратными” командами.

Задача 3. У исполнителя Аккорд две команды, которым присвоены номера:

1. отними 1

2. умножь на х

(х — неизвестное положительное число).

Выполняя первую из них, Аккорд отнимает от числа на экране 1, а выполняя вторую, умножает это число на х.

Программа для исполнителя Аккорд — это последовательность номеров команд.

Известно, что программа 12121 переводит число 4 в число 23.

Определите значение х.

Решение

Задача подобна заданиям, в которых нужно составлять программу для исполнителя при известных командах, только теперь достаточно определить одну из команд при известной программе.

1) Попробуем расписать предложенную программу для исполнителя Аккорд, подставляя пока во второй команде значения х и заполнив левую колонку заданными исходным и конечным числами:

4	1	отними 1
	2	умножь на х
	1	отними 1
	2	умножь на х
	1	отними 1
23

2) Очевидно, что для первой команды можно сразу записать результат её выполнения. Точно так же можно определить число, которое было перед выполнением последней команды:

4	1	отними 1
3	2	умножь на х
	1	отними 1
	2	умножь на х
24	1	отними 1
23

3) Вместо оставшихся числовых значений запишем соответствующие математические выражения и определим, какое математическое выражение должно давать известное нам предпоследнее число:

4	1	отними 1
3	2	умножь на х
3х	1	отними 1
3x - 1	2	умножь на х
х(3х - 1) = 24	1	отними 1
23

4) Тем самым мы получили “ключевое” уравнение, позволяющее вычислить х:

X(3X - 1) = 24.

Решаем его как обычное квадратное уравнение:

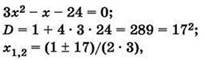
тогда

Поскольку указано, что х — это положительное число, нам подходит только значение 3.

Ответ: 3.

Задача 4. У исполнителя У троите ль две команды, которым присвоены номера:

1. прибавь 1,

2. умножь на 3.

Первая из них увеличивает число на экране на 1, вторая — утраивает его.

Программа для У троите ля — это последовательность команд.

Сколько есть программ, которые число 1 преобразуют в число 29?

Ответ обоснуйте.

Решение

Для решения можно построить полное дерево вариантов для получения числа 1 из числа 29 (не “обрубая” повторяющиеся ветви!) и подсчитать количество возможных способов получения этого числа (количество ветвей, равное количеству конечных вершин с учётом всех повторяющихся значений).

Хотя данный способ наиболее понятен и нагляден, для получения максимального балла на экзамене требуется запись аналитического решения задачи.

Пусть R(n) — количество программ, которые преобразуют число 1 в число n.

Для анализа решения лучше (как и в предыдущих задачах) рассматривать обратный процесс — получение числа 1 из числа 29 при помощи обратных команд “вычесть 1” и “делить на 3”.

Тогда R(n) = R(n/3) + R(n - 1) {в общем случае очередное число может быть получено или делением на 3, или вычитанием единицы}.

Возвращаясь к исходной задаче, расписывается каждый из шагов последовательности действий для получения числа 29 из числа 1.

R(1) = 1 {в любом случае исходное число — “в единственном экземпляре”}.

R(2) = R(2/3) + R(2 - 1) = R(2/3) + R(2 - 1) = R(2 - 1) = R(1) = 1 {слагаемые, дающие нецелый результат, исключаются; для получаемого значения R(n) берётся ранее вычисленное значение}.

Ответ: 23 программы.

Задача 5. У исполнителя “Троитель-шестеритель” две команды, которым присвоены номера:

1. прибавь 6,

2. умножь на 3.

Первая из них увеличивает число на экране на 6, вторая — утраивает его.

Программа для исполнителя — это последовательность команд.

Сколько есть программ, которые число 9 преобразуют в число 87?

Ответ обоснуйте.

Решение

Строится аналогично предыдущей задаче. Поскольку предполагается прибавление не 1, а 6, нужно записывать значения R(n) для n с шагом 6.

R(9) = 1 {в любом случае исходное число — “в единственном экземпляре”}.

R(9 + 6) = R (15) = R (15/3) + R (15 - 6) = R(5) + R(9) = R(9) = 1 {очередную строку записываем для значения п, увеличенного на 6; слагаемые, дающие нецелый результат, исключаются; для получаемого значения R(n) берётся ранее вычисленное значение; если значение R(n) не существует, то оно исключается}.

Почему нужно расписывать значения R(n) с шагом, равным 6, а не 1?

Если использовать шаг 1, то получим запись:

R(10) = R(10/3) + R(10 - 6) = R(4).

Поскольку вычисления начинаются с числа 9, значение R(4) не существует, и данная запись бессмысленна. Аналогично, несуществующие значения R(n) получаются и в других случаях при попытке записи строк для п с шагом, отличающимся от 6.

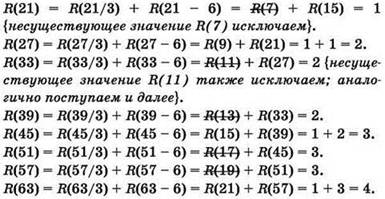
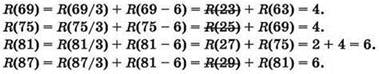
Ответ: 6 программ.

Задача 6. У исполнителя Квадратик две команды, которым присвоены номера:

1. прибавь 2,

2. возведи в квадрат.

Первая из них увеличивает число на экране на 2, вторая — возводит в квадрат.

Программа для исполнителя — это последовательность команд.

Сколько есть программ, которые число 4 преобразуют в число 66?

Ответ обоснуйте.

Решение

Записываются строки, содержащие “обратные” операции вычитания пятёрки и вычисления корня квадратного. Кроме того, поскольку в исходной задаче прибавляется число 2, нужно записывать такие строки начиная с исходного числа 4 и с шагом 2.

R(4) = 1 {в любом случае исходное число — “в единственном экземпляре”}.

R(4 + 2) = R(6) = R(√6) + R(6 - 2) = R(√6) + R(4) = R(4) = 1 {очередную строку записываем для значения n, увеличенного на 2; слагаемые, где квадратный корень извлекается не нацело, исключаются; для получаемого значения R(n) берется ранее вычисленное значение; если значение R(n) не существует, то оно исключается}.

Ответ: 4 программы.

Задача 7.

Исполнитель Числовик преобразует введенное число, используя две возможные команды:

1. Прибавить 1

2. Прибавить 3

(т.е. первая команда увеличивает число на 1, а вторая увеличивает его на 3).

Программа для исполнителя Числовик представляет собой последовательность номеров таких команд (например: 12122 — программа, по которой число 5 преобразуется в число 5+1+3+1+3+3 = 16).

Траекторией вычислений мы будем называть последовательность результатов (как промежуточных, так и итогового) выполнения команд программы. Например, для программы 12122 и исходного числа 5 траектория состоит из чисел 6, 9, 10, 13, 16.

Сколько существует программ, для которых при исходном числе 3 результатом является число 10 и при этом траектория вычислений содержит число 8?

Решение (графический способ)

Наглядное решение путём построения дерева вычислений.

Построение производится, начиная с заданного исходного числа (3) и до получения в ветвях значений, равных или превышающих конечное значение (10). Требуемое промежуточное значение (8) отмечается цветом, обводкой или другим способом. По завершении построения дерева выполняется подсчёт количества его ветвей, которые содержат отмеченное промежуточное значение (8). Для подсчёта количества таких ветвей достаточно начинать с искомого конечного значения (10) и прослеживать рёбра графа вверх до встречи требуемого промежуточного значения (8).

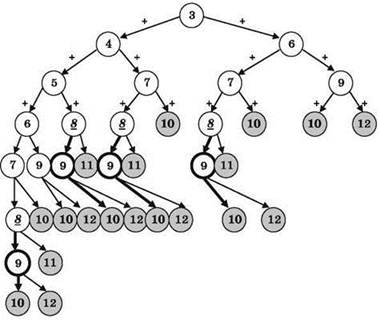
Если от нескольких конечных значений (10) можно пройти по рёбрам графа вверх до одного и того же промежуточного значения (8), то такие траектории считаются разными.

Можно сделать дерево менее громоздким, если прекращать в нём построение ветвей, в которых нет требуемого числа, но уже получилось значение, большее, чем это число.

Точно так же можно прекращать построение ветвей, в которых встретилось число, которого, согласно условию, в траектории быть не должно (такие задачи также могут встретиться на ЕГЭ).

Ответ: 4.

Задача 8.

Исполнитель Калькулятор преобразует введенное число, используя две возможные команды:

1. Прибавить 1

2. Прибавить 2

(т.е. первая команда увеличивает число на 1, а вторая увеличивает его на 2).

Сколько существует программ, для которых при исходном числе 1 результатом является число 16 и при этом траектория вычислений содержит число 6, но не содержит число 10?

Решение (“алгебраический” способ)

В предыдущих задачах требовалось просто определить количество возможных программ для исполнителя, позволяющих из заданного числа получить некоторое итоговое число. Задачу же, в которой в “траектории вычислений” должно непременно присутствовать некое “обязательное” число и/или должно обязательно отсутствовать некоторое “нежелательное” число, можно решать тем же способом, но при решении учитывать эти “особые” числа.

В данной задаче исходным является число 1, конечным — число 16, “обязательным” — число 6, а “нежелательным” — число 10.

Как и ранее, обозначим R(n) — количество программ, которые преобразуют число 1 в число n. Для анализа решения будем рассматривать обратный процесс — получение числа 1 из числа 16 при помощи обратных команд “вычесть 1” и “вычесть 2”. Тогда R(n) = R(n - 1) + R(n - 2) {в общем случае очередное число может быть получено или вычитанием единицы, или вычитанием двойки}.

При этом важно понимать, что в каждой такой строке слагаемые R(n - 1) и R(n - 2) означают две возможные “траектории”, приводящие к данному числу n.

Теперь возвращаемся к задаче и расписываем каждый из шагов последовательности действий для получения числа 16 из числа 1.

R(1) = 1 {в любом случае исходное число — “в единственном экземпляре”}.

{значение не существует}.

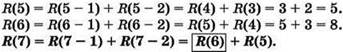
В нашей задаче требуется, чтобы в получаемых “траекториях вычисления” (т.е. в подсчитываемых программах) обязательно имелось число 6. Траектории же, которые “проходят” через число 5, нужно исключить. Поэтому слагаемое R(5) нужно приравнять нулю.

Получаем:

Продолжаем запись:

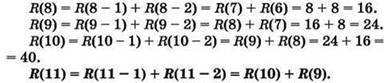
В нашей задаче число 10 в “траектории вычислений” обязательно должно отсутствовать. Поэтому слагаемое R(10) нужно приравнять нулю.

Получаем:

Аналогично:

Завершаем запись:

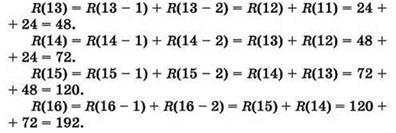
Ответ: 192 траектории.