Поиск информации в сети Интернет. Поисковые запросы - Технологии поиска и хранения информации

Конспект

Поисковый запрос для поисковой системы в Интернете представляет собой ключевое слово или несколько ключевых слов, соединенных между собой знаками логических операций И, ИЛИ, НЕ¹.

Процесс поиска в поисковой системе на основании поискового запроса аналогичен выборке данных в БД в соответствии с заданным условием отбора:

• если задано только одно ключевое слово, то производится поиск (выборка и включение в список найденного) всех web-страниц, в которых содержится данное ключевое слово;

• если ключевое слово задано с операцией НЕ, то производится поиск всех web-страниц, в которых не содержится данное ключевое слово;

• если ключевые слова связаны логической операцией И, то производится поиск web-страниц, в которых содержатся все эти ключевые слова;

• если ключевые слова связаны логической операцией ИЛИ, то производится поиск web-страниц, в которых содержится хотя бы одно ключевое слово.

Ранжирование поисковых запросов

Для разных поисковых запросов (содержащих различное число ключевых слов, связанных разными логическими операциями) количество найденных страниц будет разным. При этом важно помнить простые правила:

• операция “И” (&, Λ) сокращает объём получаемого при поиске результата (уменьшает количество найденных сайтов), причём чем больше в ней задействовано операндов, тем меньше будет объём получаемого списка найденных сайтов;

• операция “ИЛИ” (|, V) увеличивает объём получаемого при поиске результата (увеличивает количество найденных сайтов), причём чем больше в ней задействовано операндов, тем больше будет объём получаемого списка найденных сайтов.

Запросы, состоящие из одного-единственного операнда (ключевого слова) и не содержащие логических операций, можно рассматривать как запросы с операцией “ИЛИ” и с самым маленьким количеством операндов, т.е. в ранжированном списке такой запрос располагается непосредственно перед всеми остальными “ИЛИ”-запросами.

Причины этого очевидны: если операнды объединены при помощи операции “И”, то найденные документы (web-страницы) должны содержать все эти операнды (ключевые слова). Тогда, например, для запроса onepand1 & операнд2 & операнд3 получается следующий результат:

Документ содержит:			Документ найден?
операнд 1	операнд 2	операнд 3
			нет
+			нет
	+		нет
		+	нет
+	+		нет
	+	+	нет
+		+	нет
+	+	+	да

Если же операнды объединены при помощи операции “ИЛИ”, то найденные документы (web-страницы) могут содержать хотя бы один из этих операндов (ключевых слов). Тогда для запроса onepand1 | операнд2 | операнд3 результат будет таким:

Документ содержит:			Документ найден?
операнд 1	операнд 2	операнд 3
			нет
+			да
	+		да
		+	Да
+	+		Да
	+	+	Да
+		+	Да
+	+	+	да

Таким образом, для поисковых запросов, включающих в себя только один вид логических операций (только “И” или только “ИЛИ”) можно сразу определить их место в формируемом списке ранжирования. Если в задаче требуется расположить запросы по возрастанию² количества найденных документов, то:

• запросы с операцией “И” будут располагаться в начале списка, и чем больше в них задействовано операндов, тем такие запросы ближе к началу списка;

• запросы с операцией “ИЛИ” будут располагаться в конце списка, и чем больше в них задействовано операндов, тем такие запросы ближе к концу списка;

• запрос из одного-единственного ключевого слова будет располагаться в списке непосредственно перед запросами с операцией “ИЛИ”.

Более сложен случай, когда поисковые запросы содержат оба типа логических операций — и “И”, и “ИЛИ”.

Иногда можно было получить правильный ответ просто методом исключения: такой смешанный запрос располагается в ранжированном списке где-то посередине — между расположенным в его начале блоком запросов с “И” и расположенным в конце блоком запросов с “ИЛИ”.

Возможны задачи, в которых смешанных запросов будет предложено несколько. В этом случае надо немного порассуждать, как ранжировать такие смешанные запросы между собой.

Пример. Имеются два смешанных запроса:

(кошки & собаки) | кролики

и

(кошки | собаки) & кролики

В первом случае будут найдены документы, в которых есть оба слова — “кошки” и “собаки”, и к ним будут добавлены все документы со словом “кролики”.

Во втором случае будут найдены документы, содержащие или слово “кошки”, или слово “собаки”, а из них будут отобраны только те документы, которые содержат также слово “кролики”.

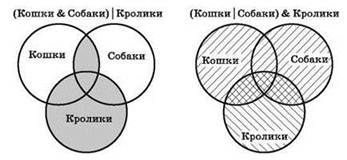
Можно считать, что “действие” (уменьшение или увеличение количества найденных документов) логических операций “И” и “ИЛИ” “ослабляется”, когда они стоят в скобках, и “усиливается”, когда эти операции расположены вне скобок. То есть когда операция “И” стоит в скобках, а “ИЛИ” — вне скобок, будет найдено больше документов, чем когда операция “ИЛИ” стоит в скобках, а “И” — вне скобок.

Вычисление количества найденных страниц

В подобных задачах считается, что существует некоторое ограниченное количество web-документов, часть которых (в том числе все они либо ни один из них) может быть найдена при помощи определённого поискового запроса. В задаче рассматривается набор запросов, включающих одни и те же ключевые слова (полный или неполный набор) и связанных различными логическими операциями. Для этих запросов указаны количества найденных документов, а по одному из запросов это количество требуется определить.

В этом случае найденные по каждому элементарному запросу (по какому-то одному ключевому слову) web- документы рассматриваются как пересекающиеся (операция И) либо объединяемые (операция ИЛИ) множества, а количества найденных документов вычисляются как объёмы этих множеств и/или их подмножеств.

Пример:

В таблице приведено количество страниц, которое поисковая система находит по каждому запросу.

Запрос	Количество найденных страниц
Кошки | Собаки | Кролики	2600
Кошки	1300
Собаки	800
Кролики & Кошки	300
Собаки & Кошки	200
Кролики & Собаки	200
Кролики & Собаки & Кошки	100

Требуется определить, какое количество страниц будет найдено по запросу “Кролики”?

Совокупность запросов можно представить в виде диаграммы Эйлера-Венна (ключевым словам соответствуют пересекающиеся круги), а получившиеся при этом области нумеруются. Для нумерации используются цифры в кружках.

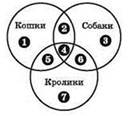
Области, соответствующие отдельным ключевым словам (кругам), а также области попарных пересечений кругов, соответствующие составным запросам с операцией И, состоят из нескольких пронумерованных областей. Например, круг “Кошки” — это объединение областей 1, 2, 4 и 5, а пересечение кругов “Кошки” и “Собаки” — это объединение областей 2 и 4. Аналогично, составным запросам с операцией ИЛИ соответствуют объединения пронумерованных областей, относящихся ко всем использованным в запросе ключевым словам. Например, запросу “Кошки | Собаки” соответствует объединение областей 1, 2, 3, 4, 5 и 6 (причём каждая пронумерованная область берётся только по одному разу).

Такие объединения пронумерованных областей записываются как суммы соответствующих порядковых номеров (цифр в кружках).

Далее для выполнения расчётов количеств запросов номера областей (цифры в кружочках) рассматриваются как своеобразные переменные, значения которых равны количествам запросов, приходящихся на каждую такую область. Тогда приведённую в условии таблицу запросов можно преобразовать в систему уравнений:

Запрос	Уравнение	Комментарий
Кошки | Собаки | Кролики	1 + 2 + 3 + 4 + 5 + 6 + 7 = 2600	Все области, соответствующие всем трём кругам
Кошки	1 + 2 + 4 + 5 = 1300	Области, соответствующие кругу “Кошки”
Собаки	2 + 3 + 4 + 6 = 800	Области, соответствующие кругу “Собаки”
Кролики & Кошки	4 + 5 = 300	Области, соответствующие пересечению кругов “Кошки” и “Кролики”
Собаки & Кошки	2 + 4 = 200	Области, соответствующие пересечению кругов “Кошки” и “Собаки”
Кролики & Собаки	4 + 6 = 200	Области, соответствующие пересечению кругов “Собаки” и “Кролики”
Кролики & Собаки & Кошки	4 = 100	Область пересечения всех трёх кругов (в центре диаграммы)

Соответственно, искомый запрос “Кролики” соответствует сумме: 4 + 5 + 6 + 7 (области, соответствующие кругу “Кролики”).

Решение задачи сводится к решению получившейся системы уравнений путём подстановок известных значений переменных и/или их сумм. Как правило, не обязательно доводить решение системы до вычисления значений всех переменных по отдельности, — достаточно подстановками заменить числами все переменные в искомой сумме, а затем произвести её вычисление.

В данном случае решение может быть таким:

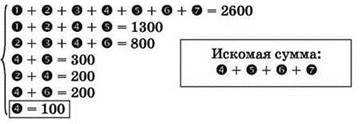
Во все уравнения подставляется известное значение 4:

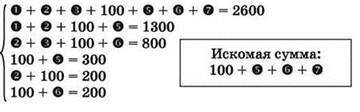
Вычисляются значения 2, 5 и 6 и подставляются в остальные уравнения:

Из второго и третьего уравнений определяются значения 1 и 3 и подставляются в первое уравнение:

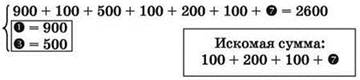
Из первого уравнения вычисляется значение 7 и подставляется в запись искомой суммы:

Таким образом, в искомой сумме все переменные заменены числовыми значениями:

100 + 200 + 100 + 700 = 1100.

Ответ: запросу “Кролики” соответствует 1100 найденных страниц.

Разбор типовых задач

Задача 1. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:

Ключевое слово	Количество сайтов, для которых данное слово является ключевым
скутер	200
байк	250
мопед	450

Сколько сайтов будет найдено по запросу

(байк | скутер) & мопед

если по запросу байк | скутер было найдено 450 сайтов, по запросу байк & мопед — 40, а по запросу скутер & мопед — 50 сайтов?

Решение

В этом случае вид диаграммы Венна будет другим — она будет состоять из трёх кругов:

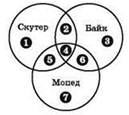
Составляется система уравнений для каждого заданного запроса (как в таблице, так и вне её), не забывая также добавить условие, что всего сайтов было 1000:

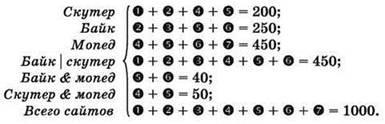
Запрос (байк |скутер) & мопед при этом соответствует выражению:

Решается система уравнений.

Из четвёртого уравнения вычитаются первые два:

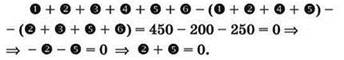
Значения наших “переменных”, обозначенных цифрами в кружках, — это количества найденных документов (т.е. числа натурального ряда), которые не могут быть отрицательными. Следовательно, если сумма таких “переменных” равна нулю, то все переменные, входящие в эту сумму (в данном случае 2 и 5), также обязаны равняться нулю. Следовательно:

Это является объяснением тому, что диаграмма Венна называется “примерной”: равенство нулю этих двух “переменных” означает, что запросу байк & скутер не соответствует ни один документ (сайт), т. е. диаграмма Венна на самом деле должна выглядеть так:

Складывается пятое и шестое уравнения, одновременно подставляя уже известное нулевое значение “переменной” 5:

С учётом нулевого значения “переменной” 5 — это и есть значение искомого выражения для запроса

(байк | скутер) & мопед.

Задача решена. При необходимости, “расплетая” систему уравнений дальше, можно было бы вычислить значения всех используемых “переменных” — от 1 до 7 — и определить количества найденных документов для любого запроса с указанными ключевыми словами.

Ответ: 90.

Задача 2. В языке запросов поискового сервера для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” — символ “&”.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Кол-во найденных страниц, тыс.
Паскаль & (Си & Бейсик \ Кобол)	350
Паскаль & Кобол	187
Паскаль & Си & Бейсик & Кобол	48

Какое количество страниц (в тысячах) будет найдено по запросу

Паскаль & Си & Бейсик?

Считаем, что все запросы выполнялись почти одновременно и набор страниц, содержащих искомые слова, за это время не изменялся.

Решение

“Традиционное” решение такой задачи — построение кругов Эйлера. Но здесь — целых четыре переменных, а числовых данных явно недостаточно, чтобы выполнить полное решение. Как же быть?

Обратим внимание на запрос Паскаль & (Си & Бейсик | Кобол) и раскроем скобки в этом логическом выражении: Паскаль & Си & Бейсик | Паскаль & Кобол.

А теперь посмотрим на запрос Паскаль & Си & Бейсик & Кобол. Правда, похоже? И там, и там слева стоит “Паскаль & Си & Бейсик”. А если сравнить со вторым запросом — Паскаль & Кобол, то мы увидим: в первом запросе справа от “|” записано “Паскаль & Кобол” (как во втором запросе), а в третьем запросе правая часть — только “Кобол”. Но ведь существует “правило поглощения”: А & В & А = А & В (повторяющийся операнд А можно не повторять). А значит, верно и обратное: любой операнд можно повторить (записав через тот же знак операции) сколько угодно раз, не меняя значение логического выражения!

Воспользуемся этим и повторим в третьем запросе слово Паскаль: Паскаль & Си & Бейсик & Паскаль & Кобол. Значение выражения не изменилось, но зато его теперь можно представить в виде: (Паскаль & Си & Бейсик) & (Паскаль & Кобол).

Итак, четыре наших запроса (включая искомый) теперь выглядят так:

Паскаль & Си & Бейсик | Паскаль & Кобол

Паскаль & Кобол

(Паскаль & Си & Бейсик) & (Паскаль & Кобол)

Паскаль & Си & Бейсик

Совершенно очевидно, что можно выполнить “макроподстановку” :

А = Паскаль & Си & Бейсик,

В = Паскаль & Кобол

Тогда наши запросы примут вид:

А | В (350 тыс.стр.),

В (187 тыс.стр.),

А & В (48 тыс.стр.),

А — искомый.

Теперь мы получили задачу всего с двумя логическими переменными (и, соответственно, с двумя кругами Эйлера):

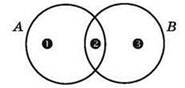
А | В	1 + 2 + 3	350 тыс.стр.
В	2 + 3	187 тыс.стр.
А & В	2	48 тыс.стр.
А	1 + 2	Требуется найти

Составляем уравнения:

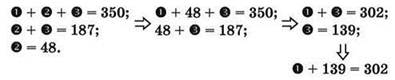
Отсюда легко вычислить, что 1 = 163, а 1 + 2 = 163 + 48 = 211.

Следовательно, по запросу Паскаль & Си & Бейсик будет найдено 211 тыс.стр.

Ответ: 211.

Задача 3. В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдёт поисковый сервер по каждому запросу.

Для обозначения логической операции “ИЛИ” в запросе используется символ |, а для логической операции “И” — символ &.

1	канарейки | щеглы | содержание
2	канарейки & содержание
3	канарейки & щеглы & содержание
4	разведение & содержание & канарейки & щеглы

Решение

Запросы с операцией “И” в списке, ранжированном по возрастанию количества найденных документов, располагаются в самом начале, и чем больше в эти запросы включено операндов, тем они ближе к началу списка. Значит, список будет начинаться с запросов 4, 3 и 2 (именно в этом порядке).

Запросы с операцией “ИЛИ” располагаются в конце ранжированного списка, — значит, запрос 1 будет последним.

Смешанные по типу операций запросы (при их наличии) определяются по методу исключения и располагаются в списке посередине между запросами с “И” и запросами с “ИЛИ”.

Ответ: 4321.

---

¹ Язык поисковых запросов, реализованный на почтовых сервисах (Яндекс, Google и пр.), включает также ряд других операций с ключевыми словами, позволяющих осуществлять поиск более гибко.

² Если требуется, наоборот, выстроить поисковые запросы по порядку уменьшения количества найденных документов, то задача решается аналогично, но расположение запросов в списке будет обратным.