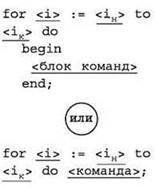Циклы: анализ алгоритмов - Программирование

Конспект

Цикл с предусловием (цикл ПОКА)

Обеспечивает выполнение блока команд, составляющего тело цикла, пока условие остается истинным (выход из цикла — по ложности условия).

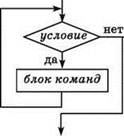
Условие проверяется до начала выполнения цикла, поэтому возможна ситуация, что тело цикла не будет выполнено ни разу.

Цикл с постусловием (цикл ДО)

Обеспечивает выполнение команд, составляющих тело цикла, пока условие не станет истинным (цикл выполняется, пока условие ложно).

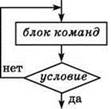
Условие проверяется после выполнения цикла, поэтому тело цикла всегда выполняется хотя бы один раз.

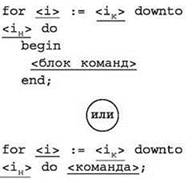
Цикл с параметром (цикл со счётчиком, цикл ДЛЯ)

Обеспечивает выполнение блока команд, составляющего тело цикла, количество раз, заданное начальным, конечным значениями переменной-счётчика (параметра цикла) и шагом её изменения.

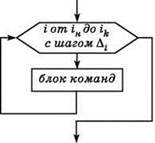
Первоначально переменной-счётчику (в данном примере — переменной i) присваивается начальное значение i_H и выполняется тело цикла. После выполнения тела цикла значение счетчика увеличивается на заданную величину шага Δi и выполняется проверка: не превысило ли значение счётчика заданное конечное значение i_K. Если не превысило, то вновь выполняется тело цикла. Иначе происходит выход из цикла.

Конструкции циклов в языке Паскаль

Цикл с предусловием:

Цикл с постусловием:

Цикл со счётчиком:

Цикл с шагом 1	Цикл с шагом —1

Операторы досрочного завершения цикла

Оператор языка Паскаль	Описание
continue	Оператор продолжения — выполнение данного оператора прекращает текущее выполнение тела цикла и передаёт управление на проверку условия цикла
break	Оператор прерывания — выполнение данного оператора прекращает выполнение цикла и передаёт управление на следующий оператор после цикла

Разбор типовых задач

Задача 1. Ниже записан алгоритм. Получив на вход число х, этот алгоритм печатает два числа: а и b. Укажите наименьшее из таких чисел х, при вводе которых алгоритм печатает сначала 13, а потом 5.

Решение

Очевидно, здесь из числа х сначала выделяется последняя цифра, а в переменной а, таким образом, накапливается сумма цифр исходного числа, после чего в числе х очередная последняя цифра отбрасывается. То есть программа выполняет “разборку” заданного числа на отдельные цифры. Но здесь нет “обычного” счётчика проходов цикла. Зато появился оператор if.

В этом условном операторе выполняется проверка: если только что выделенная цифра меньше текущего значения b (а вначале так и будет: исходное b = 10 и больше, чем любая возможная десятичная цифра), то эта цифра перезапоминается в b. А дальше такое перезапоминание будет производиться, только если очередная (т.е. более “старшая” по разрядам) цифра числа х будет меньше, чем более “младшие” (запомненные в b ранее).

Теперь смотрим, что программа выводит на экран. Сначала это число а — сумма цифр числа х, равная 13. А потом — число b, указывающее что одна из этих цифр — цифра 5, причём она — наименьшая из всех цифр в числе х (однако количество этих цифр нам неизвестно).

Можно ли по этим данным определить число х! Да, можно! Если одна из цифр равна 5, то, вычтя её из суммы (13), мы получаем число 8. Это сумма всех остальных цифр числа х. Какими же они могут быть и сколько их может быть? Перебираем варианты:

• 1 + 7 — невозможно: тогда в Ь была бы запомнена наименьшая по величине цифра 1, а не 5; то же касается и вариантов 2 + 6, 3 + 5, 4 + 4 и всех им “симметричных” (например, 5 + 3) — во всех них есть хотя бы одна цифра, меньшая 5;

• 1 + 1 + 6, 1 + 2 + 5 и все прочие возможные варианты с тремя цифрами: тоже невозможны по той же причине;

• очевидно, точно так же невозможны и любые другие варианты, в которых остаток суммы, равный 8, раскладывается на несколько цифр.

Следовательно, остается одна-единственная возможность: число х — двузначное и содержит цифры 5 и 8.

А какое из подобных чисел — наименьшее? Очевидно, 58 (а не 85)!

Ответ: 58.

Задача 2. Имеется алгоритм. Получив на вход число х, он печатает два числа а и b. Нужно указать наибольшее из чисел х, при вводе которого алгоритм напечатает сначала 2, а потом 26.

Решение

Вновь проанализируем алгоритм. В операциях mod и div вторым операндом является число 100, а не 10. Следовательно, теперь в цикле обрабатываются не отдельные цифры исходного числа, а числа, составленные из пар таких цифр.

Значение переменной а равно 2. Значит, в исходном числе (раз оно разбивается на пары) может быть или четыре цифры, или три (вторая по счету выделяемая пара — неполная). Нам, по условию, нужно искать наибольшее из возможных чисел, — значит, нужно пытаться брать в рассмотрение число из наибольшего количества цифр — из четырёх.

Сумма числа, которое составлено из двух последних цифр, и числа, составленного из первых двух цифр, равна 26. Но максимально возможная сумма десятичных цифр — это 18 (9 + 9). Нам нужно получить как можно большее возможное значение х, а значит, наибольшие цифры должны стоять в нём в начале числа. Предположим, что эти первые цифры — и есть две девятки. Тогда второе число из пары цифр будет равно 26 - 18 = 8.

Задача практически решена. Остаётся записать два найденных двузначных числа так, чтобы составить из них требуемое число х: 9908 (не забываем во второй паре дописать нуль, чтобы превратить “одинокую” восьмерку в двузначное число).

Ответ: 9908.

Задача 3. Ниже на пяти языках записан алгоритм. Получив на вход число х, этот алгоритм печатает два числа а и b. Укажите наибольшее из таких чисел х, при вводе которых алгоритм печатает сначала 4, а потом 20.

Решение

Анализируем алгоритм.

Очевидно, что переменная а представляет собой счётчик количества проходов цикла.

В самом цикле сначала выполняется проверка чётности числа (т.е. фактически — чётности его последней цифры). Если число (и последняя его цифра) чётно, то последняя цифра числа выделяется (х mod 10) и прибавляется к переменной b. После этого, уже вне условного оператора, из числа х отбрасывается последняя цифра (х div 10). Таким образом, в программе выполняется подсчёт суммы чётных цифр введённого числа.

Поскольку в результате на экран выводится пара чисел 4 и 20, делаем вывод, что количество цифр в исходном числе (определяющее количество проходов цикла) равно 4, а сумма чётных цифр в этом числе равна 20.

Остаётся найти наибольшее из возможных четырёхзначных чисел, в котором сумма чётных цифр равна 20.

Вспоминаем правило: в большем числе цифры расположены по убыванию.

Поэтому нам “выгодно” выделить в составе суммы 20 одно число — чётное и соответствующее наибольшему из возможных значению чётной десятичной цифры (очевидно, это 8). Оставшуюся часть суммы (12) проверяем: может ли она соответствовать какой-либо чётной цифре. В нашем случае она превышает максимально возможное значение чётной цифры (8). Поэтому мы снова выделяем из этой суммы чётное и наибольшее из возможных значение 8. Остаётся число 4. Таким образом, мы разбиваем сумму 20 на три слагаемых: 8+8+4.

Таким образом, мы определили три чётных цифры, входящих в исходное число. Оставшаяся четвёртая цифра должна быть нечётной. И поскольку нам требуется наибольшее исходное число из возможных, а нечётные цифры на подсчёт суммы не влияют, мы можем выбрать эту цифру равной 9.

Итак, мы имеем четыре цифры: 8, 8, 4 и 9. Остаётся расположить их по убыванию, чтобы получить число 9884. Оно и будет наибольшим из возможных, которое в результате работы указанной программы даст на экране значения 4 и 20.

Ответ: 9884.

Задача 4. Ниже на пяти языках записан алгоритм. Получив на вход число х, этот алгоритм печатает два числа а и b. Укажите наименьшее из таких чисел х, при вводе которых алгоритм печатает сначала 6, а потом 18.

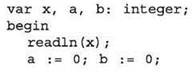
Решение

Как и в предыдущей задаче, алгоритм — тот же самый: переменная а — это счётчик количества проходов цикла и следовательно, количество цифр в исходном числе (6 прохода — четырёхзначное число), а в переменной Ъ подсчитывается сумма чётных цифр числа. Однако теперь нужно найти наименьшее из возможных четырёхзначных чисел, в котором сумма чётных цифр равна 18.

Вспоминаем правило: в меньшем числе цифры расположены по возрастанию, при этом самая первая цифра должна быть ненулевая, наибольшие цифры должны быть “сгруппированы” в конце числа (справа), а начальные цифры (кроме самой первой) “выгодно” заполнять нулями.

Наша сумма (18) превышает возможное наибольшее значение чётной цифры (8). Пробуем выделить из этой суммы слагаемое, равное 8 (которое возьмём в качестве последней цифры). Остаётся 10. Это число тоже превышает возможное наибольшее значение чётной цифры, поэтому из него мы снова выделяем слагаемое 8 (это будет предпоследняя цифра числа). Остаётся число 2, которое может являться чётной десятичной цифрой. Таким образом, мы разбили сумму 18 на три слагаемых: 8+8+2.

Три цифры исходного числа нам известны. Осталось определить ещё две. Одну из них берём ненулевую, наименьшую возможную нечётную — это единица. Она в создаваемом числе будет самой первой, а на подсчёт суммы не влияет. Ещё одну цифру “заполняем” нулём.

Остаётся записать полученные цифры (8, 8, 2, 1, 0) в таком порядке, чтобы получилось наименьшее из возможных пятизначных чисел. Это число 10288.

Ответ: 10288.

Задача 5. Имеется алгоритм. Получив на вход число х, он печатает два числа а и b. Нужно указать наименьшее из таких чисел х, при вводе которого алгоритм напечатает сначала 2, а потом 3.

Решение

Здесь алгоритм совершенно другой. Подсчёт количества проходов цикла не ведётся вообще. В переменную с записывается остаток от деления текущего значения числа х на 2, а затем если с = 0, то на единицу увеличивается значение а, а если с = 1, то на единицу увеличивается значение b (которые в итоге и выводятся на экран). А после этого у исходного числа х отбрасывается последняя цифра.

Нетрудно догадаться, что данный алгоритм, последовательно выделяя из исходного числа отдельные цифры, определяет чётность каждой такой цифры и подсчитывает в переменной а количество чётных, а в переменной b — количество нечётных цифр. По условию, чётных цифр в этом числе — 2, а нечётных — 3.

Не менее очевидно, что сумма итоговых значений а и b дает нам общее количество цифр в числе: 2 + 3 = 5.

Итак, нам нужно найти наименьшее из возможных 5-значных чисел, в котором две четных цифры и три нечётных. Какие это могут быть цифры и как они расположены в числе?

Очевидно, что для получения наименьшего возможного числа надо брать и наименьшие возможные цифры. Наименьшая нечётная цифра — это единица. А наименьшая чётная? Если учесть, что остаток от деления нуля на 2 тоже равен нулю, то в качестве наименьшей чётной цифры у нас в таких задачах выступает нуль.

Итак, в числе х должно быть три единицы и два нуля. В каких разрядах их расположить? Самой первой цифрой, очевидно должна стоять ненулевая — то есть в старшем разряде будет единица. А остальные цифры располагаем по правилу: в наименьшем возможном числе цифры по разрядам нужно располагать по возрастанию слева направо (чтобы в старших разрядах, “вес” которых максимален, оказывались самые маленькие цифры). Значит, после “лидирующее” обязательной единицы (которая определяет пятизначность числа) сначала надо записать оба нуля, а в конце — две оставшиеся единицы. Получим число 10011 (обратим внимание — десятичное).

Ответ: 10011.

Задача 6. Имеется алгоритм. Получив на вход число х, он печатает два числа а и Ь. Нужно указать наибольшее из таких чисел х, при вводе которого алгоритм напечатает сначала 3, а потом 4.

Решение

Нетрудно найти, что в искомом числе х имеется три чётных цифры и четыре нечётных, а само число — семизначное.

Теперь нам требуется найти наибольшее возможное число, значит, и цифры для него надо выбирать наибольшие из возможных. Самая большая нечётная цифра — это 9, а самая большая чётная цифра — 8.

Остаётся только правильно записать эти три восьмерки и четыре девятки. В наибольшем числе из возможных цифры записываются слева направо по убыванию (чтобы в старших разрядах, “вес” которых максимален, оказывались самые большие цифры). Тогда искомое число — 9999888.

Ответ: 9999888.

Задача 7. Имеется алгоритм. Получив на вход число х, он печатает два числа а и b. Нужно указать наибольшее из таких чисел х, при вводе которого алгоритм напечатает сначала 2, а потом 3.

Решение

Смотрим на алгоритм. Вместо оператора х := х div 10, который, как мы знаем, отбрасывает в десятичном числе последнюю цифру, у нас записано х := х div 8.

Первая идея, которая приходит в голову, — это пытаться отслеживать кратность при каждом очередном делении на 8 и исходя из этого пытаться определить количество цифр. Но, как легко догадаться, такая интерпретация представленного алгоритма слишком сложна и мало наглядна.

А что если мысленно представить исходное число х так, чтобы и при выполнении операции div 8 в числе отбрасывалась последняя цифра? Это вполне возможно, если число х понимать как записанное в восьмеричной системе счисления!

Вот это и есть “ключ” к решению любых задач такого типа (где в операторе х := х div ... стоит не 10, а другое число). Остальная же часть решения подобна рассмотренным выше.

По условию, в числе х (которое мы рассматриваем в восьмеричном формате!) две четные цифры и три нечётные. Значит, всего их пять. Число требуется наибольшее из возможных — значит, цифры надо брать наибольшие из возможных и располагать их в числе по правилу “большие — слева”.

Самая большая четная восьмеричная цифра — это 6. Самая большая нечётная восьмеричная цифра — 7. Тогда наибольшее пятизначное число, составленное из этих цифр — это 77766.

Остаётся только вспомнить, что мы рассматривали и “расписывали” число в восьмеричном виде, а в задаче-то имелось в виду десятичное число х. Значит, нужно восьмеричное значение 77766 преобразовать в десятичный формат: 77766₈ = 32758₁₀.

Ответ: 32758.