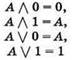Таблицы истинности. Законы алгебры логики. Задачи, решаемые с использованием таблиц истинности - Основы логики

Конспект

В алгебре логики изучаются логические операции, производимые над высказываниями. Такие высказывания могут быть истинными или ложными. Применяя к простым высказываниям логические операции, можно строить составные высказывания.

Основные логические операции

• Отрицание (инверсия, логическое НЕ)

Смысл операции: результат меняется на противоположный (вместо истины — ложь, вместо лжи — истина).

Обозначение: ¬.

Таблица истинности:

А	¬А
0	1
1	0

• Логическое сложение (дизъюнкция, логическое ИЛИ)

Смысл операции: результат — истина, если хотя бы один операнд — истина (операндом называется то значение или та переменная, над которым (которой) осуществляется операция).

Обозначения: V или +.

Таблица истинности:

А	В	А V В
0	0	0
0	1	1
1	0	1
1	1	1

• Логическое умножение (конъюнкция, логическое И)

Смысл операции: результат — истина, если оба операнда — истина.

Обозначения: Λ или &.

Таблица истинности:

А	В	А Λ В
0	0	0
0	1	0
1	0	0
1	1	1

• Исключающее ИЛИ (сложение по модулю 2, строгая дизъюнкция)

Смысл операции: результат — истина, если операнды различны.

Обозначения: ⊕ или ≠.

Таблица истинности:

А	В	А ⊕ В
0	0	0
0	1	1
1	0	1
1	1	0

• Следование (импликация)

Смысл операции: из лжи может следовать что угодно, а из истины— только истина.

Обозначение: →.

Таблица истинности:

А	В	А → В
0	0	1
0	1	1
1	0	0
1	1	1

• Равносильность (эквиваленция)

Смысл операции: результат — истина, если операнды одинаковы.

Обозначения: = или ↔.

Таблица истинности:

А	В	А ↔ В
0	0	1
0	1	0
1	0	0
1	1	1

Если в логическом выражении используется несколько логических операций, то их порядок определяется приоритетами логических операций:

Операцию “импликация” можно выразить через “ИЛИ” и “НЕ”:

Операцию “эквиваленция” также можно выразить через “ИЛИ” и “НЕ”:

Основные законы алгебры логики

Законы коммутативности
Законы ассоциативности
Законы дистрибутивности
Закон непротиворечия (высказывание не может быть одновременно истинным и ложным)
Закон исключения третьего (либо высказывание, либо его отрицание должно быть истинным)
Закон двойного отрицания
Законы де Моргана
Законы рефлексивности (идемпотенции)
Свойства логических констант 1 и 0
Законы поглощения

Связь алгебры логики с программированием

В большинстве существующих языков программирования предусмотрены функции для реализации основных логических операций (“НЕ” — NOT, “И” — AND, &, “ИЛИ” — OR, |, “Исключающее ИЛИ” — XOR, ∧), позволяющих обрабатывать данные логического типа (Boolean). При этом обычно считается, что значение “ложь” (FALSE) связано с целочисленным значением 0, а значение “истина” (TRUE) — с целочисленным значением 1 (или любым ненулевым).

В программировании подобные логические операции широко используются вместе с операторами сравнения для формирования логических условий (в командах ветвления, циклах с пост- или предусловием и пр.), а также собственно для обработки логических данных. При этом синтаксис многих языков программирования допускает сложные конструкции из оператора присваивания и операций сравнения, например в языке БЕЙСИК является корректной запись:

X = (А = В)

Она означает, что выполняется сравнение значений переменных А и Б и при их равенстве (для текстовых данных — совпадении) переменной X присваивается логическое значение “Истина” (иначе — “Ложь”).

Кроме операций над логическими данными, в некоторых языках программирования (например, Java или Си) также предусмотрены побитовые логические операции, при которых целочисленные операнды рассматриваются как двоичные числа, выбранная логическая операция производится для каждой соответствующей по номеру позиции в числе пары битов, а результат представляет собой также целое число.

Применение алгебры логики при решении задач

Законы алгебры логики могут применяться при решении различных задач, связанных с принадлежностью точки заданному интервалу либо области, при определении выполнения или невыполнения заданного правила и т.д.

Примеры.

1. При решении задач типа “Какое из приведённых имён удовлетворяет логическому условию: ¬(последняя буква гласная → первая буква согласная) Λ вторая буква согласная” достаточно для каждого из трёх упомянутых в условии правил предусмотреть логическую переменную, значение которой равно 1 “Истина”, если данное правило выполнено для конкретного имени, либо 0 (“Ложь”), если данное правило не выполнено для конкретного имени, и далее вести обработку согласно правилам алгебры логики значений этих переменных.

2. При решении задач типа “Для какого из указанных значений X истинно высказывание: ¬((X > 2) → (X > 3))” аналогичным образом выделяются логические переменные, соответствующие каждой из приведённых в условии операций сравнения для тех или иных граничных и внутриинтервальных значений числовой переменной X, после чего полученные значения этих логических переменных обрабатываются согласно правилам алгебры логики.

3. При решении задач об определении принадлежности точек интервалу на числовой прямой либо области плоскости, заданной системой неравенств (задачи группы С1) логические операции используются при формировании требуемого условия, определяющего нужную область.

Правила, которыми нужно руководствоваться при решении логических задач с интервалами:

1) при обмене местами левой и правой частей неравенства его знак меняется на противоположный;

2) если неравенство является ложным, то эквивалентное ему истинное неравенство не только имеет противоположный знак, но и становится из строгого нестрогим и наоборот; то же самое происходит при замене истинного неравенства эквивалентным ему ложным;

3) соединение компонентов логического выражения операцией “И” соответствует пересечению интервалов их истинности (интервалов значений, при которых эти компоненты истинны); соединение компонентов логического выражения операцией “ИЛИ” соответствует объединению интервалов их истинности;

4) интервал ложности представляет собой всю часть числовой прямой, кроме интервала истинности этого выражения, — производится вычитание интервала истинности из числовой прямой; аналогично определяется интервал истинности по интервалу ложности.

Кроме того, при решении задач с интервалами надо внимательно читать текст условия: если в вопросе фигурирует, например, “наибольшее натуральное число X” или “наибольшее целое положительное число X”, то это означает добавление дополнительного условия: X > 0.

Разбор типовых задач

Задача 1. Для таблицы истинности функции F известны значения нескольких ячеек:

х1	х2	х3	х4	F
	1	0		1
0	1			1
1	0			0
	0		1	0

Каким выражением может быть F?

Решение

Смысл решения — по очереди “примерять” каждый из предложенных вариантов ответа к таблице истинности и смотреть: если при указанных в ней значениях переменных хоть в какой-нибудь строке не получается требуемое значение F, то данное значение не подходит. Если же для всех строк таблицы истинности и всех имеющихся в ней значений переменных требуемое значение Fполучается, то мы считаем, что такое логическое выражение может соответствовать этой таблице и, соответственно, является решением задачи.

Чтобы ускорить решение, вспомним: для логической операции И “критическим” значением является нуль: если хотя бы одна переменная равна нулю, то и всё выражение тоже равно нулю. Аналогично, для логической операции ИЛИ “критическим” значением является единица: если хотя бы одна переменная равна единице, то и всё выражение тоже равно единице. (Разумеется, нужно не забывать заменять нуль на единицу и единицу на нуль при операции отрицания.)

Поэтому достаточно при проверке вариантов ответа проверять только часть строк таблицы истинности:

• если логическое выражение составлено из операций И, то прежде всего проверяем строки таблицы истинности, в которых F = 1: если хоть в одной ячейке, соответствующей “обычной” переменной, записан 0, а в ячейке, соответствующей переменной с НЕ, записана 1, то такой вариант ответа можно отбросить сразу;

• наоборот, если логическое выражение составлено из операций ИЛИ, то прежде всего проверяем строки таблицы истинности, в которых F = 0: если хоть в одной ячейке, соответствующей “обычной” переменной, записана 1, а в ячейке, соответствующей переменной с НЕ, записан 0, то такой вариант ответа тоже можно отбросить сразу.

№	Выражение	Операция	Проверяем строки таблицы:	Комментарий	Вывод
1)		И	c F = 1	х3 = 0 (строка 1)	Не годится
2)		ИЛИ	c F = 0	х1= 1 (строка 3)	Не годится
3)		И	c F = 1	всё соответствует
4)		ИЛИ	c F = 0	х4 = 1 (строка 4)	Не годится

Итак, предполагаемый правильный ответ — выражение Проверяем его для оставшихся строк с F = 0, убеждаемся, что им оно тоже соответствует (за счёт того, что х₂ = 0).

Ответ: (вариант № 3).

Задача 2. Логическая функция задана выражением Имеется также фрагмент таблицы истинности этой логической функции, где показаны все возможные наборы значений переменных, при которых функция истинна. Требуется определить, какие переменные соответствуют каждому столбцу таблицы истинности. Для этого в качестве ответа надо записать подряд без пробелов и разделителей буквы а, b, с по порядку их записи в столбцах таблицы слева направо. Например, так: “аbс”.

???	???	???
0	0	0	1
1	0	0	1
1	1	0	1

Решение

1. Построим полную таблицу истинности заданного выражения:

а	b	с			Результат
0	0	0	0	1	1
0	0	1	0	0	0
0	1	0	0	1	1
0	1	1	1	0	1
1	0	0	0	0	0
1	0	1	0	0	0
1	1	0	0	0	0
1	1	1	0	0	0

2. В этой таблице имеется ровно три строки, в которых логическое выражения принимает значение “истина”:

а	b	с	Результат
0	0	0	1
0	1	0	1
0	1	1	1

3. Сопоставив этот фрагмент полученной таблицы с исходным, получаем порядок записи переменных в исходной таблице: bса.

Ответ: bса.

Задача 3. На числовой прямой даны два отрезка: Р = [43, 49] и Q = [44, 53].

Укажите наибольшую возможную длину отрезка А, для которого формула тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Решение

1) Для упрощения записи заменим высказывания логическими переменными: Тогда исходное логическое выражение принимает вид:

2) Избавимся от операции следования, использовав соотношение

3) Требуется тождественное равенство этого выражения единице на все числовой оси. Вспомним, что значения логических переменных равны 1 в пределах соответствующих отрезков и 0 — вне их (причём границы входят в отрезки).

Анализируем полученное уравнение

• переменные соединены операцией ИЛИ, следовательно, результат 1 будет автоматически обеспечен, если хотя бы одна из переменных — р или q — равна 1 (то есть везде, где числовая прямая “накрыта” хотя бы одним отрезком — Р или Q);

• там, где нет ни отрезка Р, ни отрезка Q (т.е. переменные р и q обе равны 0), для обеспечения истинности результата должна быть равна 1 переменная ¬а, или, соответственно, переменная а должна быть равна 0 (отрезка А не должно быть нигде, где нет ни отрезка Р, ни отрезка Q).

4) Рисуем числовую прямую и изображаем на ней отрезки Р и Q:

5) Теперь совершенно очевидно, как расположить на этой числовой прямой отрезок А, чтобы он нигде “не высовывался” за пределы области, закрытой хотя бы одним отрезком Р или Q:

6) А теперь нужно правильно вычислить длину полученного отрезка А, помня, что речь идет о прямой натуральных чисел. В данном случае это не имеет особого значения, но в других аналогичных задачах при выполнении операции отрицания границы отрезка А могут быть “выколоты” (могут не входить в отрезок), и тогда нужно при вычислении длины отрезка брать соседние натуральные граничные значения внутри отрезка. В нашем же случае конечные точки 43 и 53 входят в отрезок А.

Теперь вспомним, как мы вычисляем длину отрезка на обычной сантиметровой линейке, — например, между отметками 1 см и 3 см. Длина этого отрезка равна двум сантиметровым интервалам между указанными отметками на шкале линейки, т.е. вычисляется как разность значений. Точно так же нужно поступить и здесь, поэтому длина отрезка А равна 53 - 43 = 10.

Ответ: 10.

Задача 4. Элементами множества X являются натуральные числа. Известно, что выражение

истинно (принимает значение 1) при любом значении n. Требуется определить наименьшее возможное значение произведения элементов множества X.

Решение

Начало решения такое же, как в предыдущей задаче: введем для используемых в выражении множеств обозначения в виде латинских букв R и Q, а затем заменим записи условий принадлежности переменной п соответствующему множеству одноименными логическими переменными:

• множества:

• логические переменные:

Затем переписываем заданное логическое выражение с учётом этих замен и выполняем его упрощение, избавляясь от операции следования и (по возможности) от скобок:

Удобнее для обозначения операции отрицания использовать надчеркивание переменных, поэтому перепишем выражение в виде:

Упрощаем это выражение, пользуясь правилом замены операции следования на операцию ИЛИ

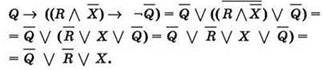
А теперь перейдём к графической части решения.

1) Рисуем числовые прямые, соответствующие множествам Q, R и X (лучше всего делать это на тетрадном листке в клеточку). Размечаем на них позиции, соответствующие всем возможным числам, используемым в множествах (в данном случае — от 1 до 10, так как наименьшее число, встречающееся в заданных множествах, равно 1, а наибольшее равно 10).

2) На числовой прямой, соответствующей множеству Q, размечаем точки по следующему правилу: для числа, которое есть в этом множестве, точка должна быть чёрной (закрашенной), а для числа, которого нет в этом множестве, точка должна быть белой (в виде пустого кружочка). Затем то же самое делаем и для числовой прямой, соответствующей множеству R.

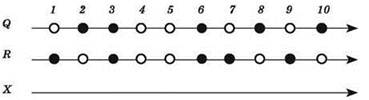
3) Смотрим на получившееся у нас логическое выражение: В нём заданные нам (в виде условий принадлежности чисел соответствующим множествам) значения связаны друг с другом и с переменной X логической операцией ИЛИ. Для гарантированной истинности этого выражения достаточно, чтобы хотя бы одно из значений — — было истинно. В нашем графическом методе действует правило: для переменной без надчеркивания (т.е. без отрицания) “истинными” являются чёрные точки, а для переменной с надчеркиванием (т.е. под отрицанием) “истинными” являются белые точки. У нас переменные Q и R записаны с надчёркиванием. Поэтому на нашем рисунке мы вычеркиваем вертикальными пунктирными линиями все такие числовые позиции, где на осях Q и R есть хотя бы одна белая точка. А в позициях, которые на числовой прямой множества X остались не зачёркнутыми, проставляем “чёрные” точки.

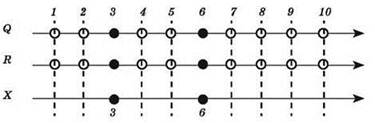
Задача практически решена: найденные значения — числа 3 и 6 — это и есть минимально необходимые элементы множества X, обеспечивающие истинность заданного выражения на всей числовой прямой для натуральных чисел.

Завершить же вычисления — подсчитать количество элементов множества X, их сумму или произведение — уже совсем просто. В нашей задаче требуется произведение — оно равно 3 ∙ 6 = 18.

Ответ: 18.