Что такое компьютер: немного истории - Предварительные сведения

Имея дело с многообразием компьютерных устройств, окружающих нас сегодня, мы часто забываем, что исходная функция компьютера — считать; большинство из нас не помнит, когда в последний раз использовали компьютер для вычислений. Впрочем, даже если попытаться это сделать, например, запустив программу “Калькулятор” или какую-нибудь цифровую таблицу вроде LibreOffice Calc или Microsoft Excel, можно заметить один любопытный факт: на рисование окошек, кнопочек, рамок таблицы и вообще на организацию диалога с пользователем компьютер при этом потратит в миллионы раз больше операций, чем на расчёты как таковые. Иначе говоря, устройство, предназначенное для проведения вычислений¹, занимается чем угодно, только не вычислениями. Понять, как так получилось, нам поможет небольшой экскурс в историю.

В качестве первой в истории вычислительной машины называют механический арифмометр Вильгельма Шиккарда, созданный в 1623 году. Машина называлась “счётными часами”, поскольку была сделана из механических деталей, характерных для часовых механизмов. “Счётные часы” оперировали шестиразрядными целыми числами и способны были производить сложение и вычитание; переполнение отмечалось звоном колокольчика. До наших дней машина не сохранилась, но в I960 году была создана работающая копия. По некоторым сведениям, машина Шиккарда могла быть и не самой первой механической счётной машиной: известны эскизы Леонардо да Винчи (XVI в.), на которых изображен счётный механизм. Был ли этот механизм воплощён в металле, неизвестно.

Самой старой из счётных машин, сохранившихся до наших дней, является арифмометр Блеза Паскаля, созданный в 1645 году. Паскаль начал работу над машиной в 1642 году в возрасте 19 лет. Отец изобретателя имел дело со сбором налогов и вынужден был проводить долгие изнурительные подсчёты; своим изобретением Блез Паскаль надеялся облегчить работу отца. Первый образец имел пять десятичных дисков, то есть мог работать с пятизначными числами. Позднее были созданы машины, имевшие до двадцати дисков. Сложение на машине Паскаля выполнялось легко, что же касается вычитания, то для него приходилось использовать метод девятичных дополнений.

Если у нас всего пять разрядов, то перенос в шестой разряд, как к заём из него, благополучно теряется, что позволяет вместо вычитания числа выполнять прибавление некоторого другого числа. Например, если мы хотим вычесть из числа 500 (то есть, на пяти разрядах, из 00500) число 134 (00134), то вместо этого можно прибавить число 99866. Если бы у нас был шестой разряд, то получилось бы 100366, но поскольку шестого разряда нет, результат получится 00366, то есть ровно то, что нужно. Как легко догадаться, “магическое” число 99866 получено путём вычитания нашего вычитаемого из 100000; с точки зрения арифметики мы вместо операции х — у выполняем х + (100000 — у) — 100000, причём последнее вычитание происходит само собой за счёт переноса в несуществующий шестой разряд.

Хитрость здесь в том, что получить из числа у число 100000 — у оказывается неожиданно просто. Перепишем выражение 100000 — у в виде 99999 — у + 1. Поскольку число у по условиям задачи не более чем пятизначное, вычитание 99999 — у в столбик произойдёт без единого займа, то есть попросту каждая цифра числа у будет заменена на цифру, дополняющую её до девятки. Останется только прибавить единичку, и дело сделано. В нашем примере цифры 00134 заменяются на соответствующие им 99865, затем прибавляется единица и получается “магическое” 99866, которое мы прибавляли к 500, вместо того чтобы вычитать 134.

На арифмометрах Паскаля вычитание выполнялось несколько хитрее. Сначала нужно было набрать девятичное дополнение уменьшаемого (число 99999 — х, для нашего примера это будет 99499), для чего барабаны с цифрами результата, видимые через специальные окошки, содержали по две цифры — основную и дополняющую до девятки, а сама машина была снабжена планкой, с помощью которой “ненужный” ряд цифр закрывали, чтобы он не отвлекал оператора. К набранному девятичному дополнению прибавлялось вычитаемое, в нашем примере 00134, то есть получалось число 99999 — х + у. Однако оператор продолжал смотреть на цифры девятичных дополнений, где отображалось 99999 — (99999 — х + у), то есть просто х — у. Для чисел из нашего примера результатом прибавления стало бы число 99633, девятичное дополнение которого — число 00366 — представляет собой верный результат операции 500 — 134.

Сейчас этот способ представляется нам чем-то вроде фокуса, любопытного, но не слишком нужного в современных реалиях. Но вот с вычислением дополнения, требующим прибавления единицы, мы ещё встретимся, когда будем обсуждать представление отрицательных целых чисел в компьютере.

Тридцать лет спустя знаменитый немецкий математик Готфрид Вильгельм Лейбниц построил механическую машину, способную выполнять сложение, вычитание, умножение и деление, причём умножение и деление выполнялись на этой машине примерно так, как мы выполняем умножение и деление в столбик — умножение производится как последовательность сложений, а деление — как последовательность вычитаний. В некоторых источниках можно встретить утверждение, что машина якобы умела вычислять квадратные и кубические корни; на самом деле это не так, просто вычислить корень, имея устройство для умножения, изрядно проще, чем без такового.

История механических арифмометров продолжалась достаточно долго и закончилась уже во второй половине XX столетия, когда механические счётные устройства были вытеснены электронными калькуляторами. Для нашего исторического экскурса важно одно общее свойство арифмометров: они не могли без участия человека проводить расчёты, состоящие из более чем одного действия; между тем решение даже сравнительно простых задач требует выполнения долгих последовательностей арифметических действий. Разумеется, арифмометры облегчали труд расчётчиков, но сохранялась необходимость выписывать на бумаге промежуточные результаты и набирать их вручную с помощью колёс, рычагов, в более поздних вариантах — с помощью кнопок.

Английский математик Чарльз Беббидж (1792-1871) обратил внимание² на то, что труд расчётчиков может быть автоматизирован полностью; в 1822 году он предложил проект более сложного устройства, известного как разностная машина. Эта машина должна была интерполировать полиномы методом конечных разностей, что позволило бы автоматизировать построение таблиц разнообразных функций. Заручившись поддержкой английского правительства, в 1823 году Беббидж начал работу над машиной, но технические сложности, с которыми он столкнулся, несколько превысили его ожидания. Историю этого проекта разные источники излагают по-разному, но все сходятся на том, что общая сумма правительственных субсидий составила огромную по тем временам сумму в 17000 фунтов стерлингов; некоторые авторы добавляют, что аналогичную сумму Беббидж потратил и из своего состояния. Факт состоит в том, что работающую машину Беббидж так и не построил, причём в ходе проекта, затянувшегося почти на два десятилетия, он сам охладел к своей затее, заключив, что метод конечных разностей — это лишь одна (пусть и важная) из огромного множества расчётных задач; следующая задуманная изобретателем машина должна была стать универсальной, то есть настраиваться на решение произвольной задачи.

В 1842 году, так и не получив никакого работающего устройства, английское правительство отказалось от дальнейшего финансирования деятельности Беббиджа. Основываясь на принципах, предложенных Беббиджем, швед Георг Шутц в 1843 году завершил построение работающей разностной машины, а в последующие годы построил ещё несколько экземпляров, один из которых продал британскому правительству, другой — правительству Соединённых Штатов. В конце XX века два экземпляра разностной машины Беббиджа были построены на основе его оригинальных чертежей, одна для музея науки в Лондоне, другая — для музея истории компьютеров в Калифорнии; таким образом было наглядно показано, что разностная машина Беббиджа могла бы работать, если бы её изготовление было завершено.

Впрочем, в историческом плане оказывается интереснее не разностная машина, а задуманная Беббиджем универсальная вычислительная машина, которую он называл аналитической. Сложность этой машины была такова, что даже выполнить её чертежи Беббиджу не удалось; задуманное устройство превосходило возможности техники того времени, да и его собственные возможности тоже. Так или иначе, именно в работах Беббиджа, посвящённых аналитической машине, во-первых, возникла идея программного управления, то есть выполнения действий, предписанных программой; и, во-вторых, появились действия, не имеющие прямого отношения к арифметике: перенос данных (промежуточных результатов) из одного устройства хранения в другое и выполнение тех или иных действий в зависимости от результатов анализа (например, сравнения) данных.

В том же году, когда британское правительство прекратило финансирование проекта разностной машины, Беббидж прочитал в университете Турина лекцию, посвящённую в основном аналитической машине; итальянский математик и инженер Федерик Луиджи Менабреа опубликовал на французском языке³ конспект этой лекции. По просьбе Беббиджа леди Августа Ада Лавлейс⁴ перевела этот конспект на английский, снабдив свой перевод развернутыми комментариями, значительно превышающими по размеру саму статью. В одном из разделов этих комментариев приводится полный набор команд для вычисления чисел Бернулли на аналитической машине; этот набор команд считается первой в истории компьютерной программой, а саму Аду Лавлейс часто называют первым программистом. Любопытно, что Ада Лавлейс, размышляя над возможностями аналитической машины, смогла уже тогда заглянуть в будущее компьютеров; помимо прочего, её комментарии содержали следующий фрагмент: “Суть и предназначение машины изменятся от того, какую информацию мы в неё вложим. Машина сможет писать музыку, рисовать картины и покажет науке такие пути, которые мы никогда и нигде не видели”. По сути, Ада Лавлейс заметила, что задуманная Беббиджем машина может рассматриваться как инструмент для обработки информации в широком смысле, тогда как решение расчётных математических задач представляет собой лишь частный случай такой обработки.

Если работающая разностная машина, как уже упоминалось выше, всё же была построена в середине XIX века, хотя и не Беббиджем, то идея программируемой вычислительной машины опередила уровень техники почти на сто лет: первые работающие вычислительные машины, управляемые программно, появились лишь во второй четверти XX века. В настоящее время считается, что хронологически первой программируемой вычислительной машиной была Z1, построенная Конрадом Цузе в Германии в 1938 году; машина была полностью механической, электричество использовалось только в моторе, приводившем механизмы в движение. Z1 использовала в работе двоичную логику, причём элементы, вычислявшие логические функции, такие как конъюнкция, дизъюнкция и т. п., были реализованы в виде наборов из металлических пластин, снабжённых хитрыми вырезами. Заинтересованному читателю мы можем порекомендовать найти в Интернете видео, демонстрирующее эти элементы на увеличенной модели: впечатление, производимое их работой, безусловно стоит потраченного времени.

Машина Z1 работала не слишком надёжно, механизмы часто заедали, искажая получаемый результат, так что практической пользы от этой машины получить не удалось, но за ней годом позже последовала Z2, использовавшая ту же механику для хранения информации (“памяти”), но осуществлявшая вычислительные операции с помощью электромагнитных реле. Обе машины выполняли инструкции, получаемые с перфоленты; перематывать ленту назад они не умели, что сильно сужало их возможности, не позволяя организовать повторения участков программы, то есть циклы. Позже, в 1941 году, Цузе построил машину Z3, использовавшую только реле и хранившую программу на пластиковой перфоленте (по некоторым данным, для этого использовалась обыкновенная киноплёнка — бракованные дубли и прочие отходы деятельности киностудий). Эта машина позволяла организовывать циклы, но не имела инструкции для условного перехода, что также несколько ограничивало её возможности. Z3 разрабатывалась в качестве секретного правительственного проекта; Цузе обратился к правительству за дополнительным финансированием с целью замены реле на электронные схемы, но в этом ему было отказано. Последняя машина в этом ряду, Z4, по своим принципам была похожа на Z3, но уже, наконец, позволяла организовать ветвление. Постройка Z4 была завершена в 1944 году, и из всех машин Конрада Цузе только она уцелела, остальные были уничтожены при бомбардировке Берлина авиацией союзников.

Долгое время о работах Цузе не было известно за пределами Германии. Между тем на окрестности Второй мировой войны пришёлся по обе стороны океана настоящий бум создания вычислительных устройств, как электромеханических (в том числе основанных на реле), так и электронных, основанных на электронно-вакуумных лампах.

Радиолампа (см. рис. 1.1) представляет собой электронный прибор, выполненный в виде запаянной стеклянной колбы с электродами, из которой откачан воздух. В простейшей радиолампе — диоде — предусмотрены два рабочих электрода (анод к катод), а также спираль, разогревающая катод до температур, при которых начинается термоэлектронная эмиссия, когда отрицательно заряженные электроны покидают катод и создают в пространстве лампы своеобразное электронное облако; под действием разности потенциалов электроны притягиваются к аноду и поглощаются им. В обратном направлении заряд передавать некому: анод, оставаясь холодным, эмиссии электронов не производит, а заряженных ионов в колбе нет, потому что там вакуум. Таким образом, через диод ток может идти только в одном направлении; поскольку заряд электрона считается отрицательным, в терминах электродинамики перемещение электрического заряда происходит навстречу электронам, то есть от анода к катоду. Если изменить полярность включения диода в цепь, то электроны, покинув разогретый электрод, тут же будут притягиваться к нему обратно под действием положительного потенциала, а до второго электрода (анода, ставшего катодом в результате переполюсовки) частицы долетать не будут, отталкиваясь от него из-за наличия на нём отрицательного потенциала.

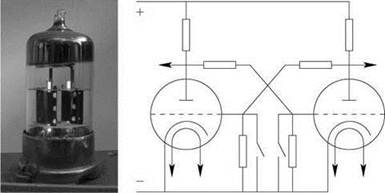
Рис. 1.1. Радиолампа (двойной триод) в действии⁵ (слева); схема триггера на двух триодах (справа)

Добавив ещё один электрод — так называемую сетку — мы получим новый тип радиолампы, называемый триодом. Сетка устанавливается внутри колбы таким образом, чтобы оказаться на пути электронов, летящих от катода к аноду. При подаче на сетку отрицательного потенциала она начинает отталкивать электроны, не позволяя им достичь анода; если подать на сетку модулированный сигнал, например, полученный с микрофона, ток, проходящий через триод, будет повторять изменения потенциала на сетке, но при этом может быть гораздо сильнее. Изначально триоды как раз и предназначались для усиления сигнала.

Взяв два триода и соединив анод каждого из них с сеткой другого, мы получим устройство, называемое триггером. Оно может находиться в одном из двух устойчивых состояний: через один из двух триодов идёт ток (говорят, что он открыт), благодаря этому на сетке второго триода имеется потенциал, не позволяющий току идти через второй триод (триод закрыт). Кратковременно подав отрицательный потенциал на сетку открытого триода, мы тем самым прекратим ток через него, в результате второй триод откроется и закроет первый; иначе говоря, триоды поменяются ролями и триггер перейдёт в противоположное устойчивое состояние. Триггер можно использовать, например, для хранения одного бита информации. Другие схемы соединения триодов позволяют построить логические вентили, реализующие конъюнкцию, дизъюнкцию к отрицание. Всё это позволяет использовать радиолампы для построения электронного вычислительного устройства.

За счёт отсутствия механических деталей машины на электронновакуумных лампах работали гораздо быстрее, но, к сожалению, сами радиолампы — предмет достаточно ненадёжный: разгерметизация колбы приводит к выходу лампы из строя; спираль, нагревающая катод, может перегореть, что также приводит к отказу лампы. Одна из первых полностью программируемых ЭВМ — ENIAC — содержала 18 000 электронных ламп, а работать машина могла только при условии, что все лампы исправны. Естественно, несмотря на беспрецедентные меры, принятые для повышения надёжности, машину очень часто приходилось ремонтировать.

Создали ENIAC американский учёный Джон Моушли и его ученик Дж. Эккерт; работы были начаты во время Второй мировой войны и финансировались военными, но, к счастью для создателей машины, завершить её до конца войны они не успели, так что проект, когда он в 1946 году был завершён, удалось рассекретить. Пионерам лампового компьютеростроения из Великобритании повезло меньше: построенные в обстановке строжайшей секретности машины Colossus Mark I и Colossus Mark II после завершения войны по личному приказу Черчилля⁶ были уничтожены, а их автор Томми Флауэрс, повинуясь всё тому же приказу, был вынужден собственноручно сжечь всю конструкторскую документацию, что сделало воссоздание машин невозможным. Широкой публике стало известно об этом проекте лишь тридцать лет спустя, а его участники лишились заслуженного признания к были фактически отлучены от мирового развития вычислительной техники. Достижения создателей Colossus к моменту рассекречивания проекта представляли разве что исторический интерес, к тому же большая их часть была утрачена при уничтожении машин и документации.

Часто можно встретить утверждение, что машины Colossus предназначались для дешифровки сообщений, зашифрованных немецкой электромеханической шифровальной машиной Enigma, а в проекте участвовал (и едва ли не руководил им) знаменитый математик, один из основоположников теории алгоритмов Алан Тьюринг. Это не так; никакого участия в проекте Colossus Тьюринг не принимал, а машина, построенная с его непосредственным участием и действительно предназначавшаяся для взлома кодов “Энигмы”, называлась Bombe, была чисто электромеханической и в принципе, строго говоря, не являлась компьютером, как и сама “Энигма”. Машины Томми Флауэрса предназначались для взлома шифрограмм, составленных с помощью машины Lorenz SZ, шифр которой был гораздо более стоек к взлому, нежели шифр “Энигмы”, и не поддавался электромеханическим методам.

Впрочем, Томми Флауэрсу действительно довелось некоторое время работать под руководством Тьюринга в одном из британских криптоаналитических проектов, и именно Тьюринг порекомендовал кандидатуру Флауэрса для проекта, связанного с Lorenz SZ.

Вычислительные машины, построенные на радиолампах, принято называть ЭВМ первого поколения; следует обратить внимание, что по поколениям различают только электронные вычислительные машины, а всевозможные механические и электромеханические вычислители к ним не относят. В частности, машины Конрада Цузе электронными не были, так что они не считаются “ЭВМ первого поколения” и вообще ЭВМ.

Возможности машин этой эпохи были весьма ограниченными: из-за громоздкой элементной базы приходилось довольствоваться мизерными (по современным меркам) объёмами памяти. Тем не менее именно к первому поколению относится одно из самых важных изобретений в истории вычислительных машин — принцип хранимой программы, который подразумевает, что программа в виде последовательности кодов команд хранится в той же самой памяти, что и данные, а сама память однородна и коды команд от данных ничем принципиально не отличаются. Машины, соответствующие этим принципам, традиционно называют машинами фон Неймана в честь Джона фон Неймана.

История названия довольно своеобразна. Одной из первых электронных машин, хранящих программу в памяти, стал компьютер EDVAC; его построили знакомые нам по ENIAC’y Моушли к Эккерт, причём обсуждение к проектирование новой машины они вели уже во время постройки ENIAC’a. Джон фон Нейман, участвовавший в качестве научного консультанта в проекте “Манхэттен”⁷, заинтересовался проектом ENIAC в том числе и потому, что проект “Манхэттен” требовал огромных объёмов вычислений, над которыми работала целая армия девушек-расчётчиц, пользовавшихся механическими арифмометрами. Естественно, фон Нейман принял активное участие в обсуждении с Моушли и Эккертом архитектурных принципов новой машины (EDVAC); в 1945 году он обобщил результаты обсуждений в письменном документе, который известен как “Первый черновик сообщения о машине EDVAC” (First Draft of the Report on theEDVAC). Фон Нейман не считал документ оконченным: в этой версии текст предназначался только для обсуждения членами исследовательской группы Моушли и Эккерта, в которую входил в числе прочих учёных Герман Голдстайн. Господствующая версия исторических событий такова, что именно Голдстайн поручил перепечатать рукописный документ, поставив на его титульном листе только имя фон Неймана (что формально правильно, поскольку автором текста был фон Нейман, но не вполне корректно в свете научных традиций, так как изложенные в документе идеи были результатом коллективной работы), и затем, размножив документ, разослал заинтересованным учёным несколько десятков копий. Именно этот документ намертво связал имя фон Неймана с соответствующими архитектурными принципами, хотя, судя по всему, фон Нейман не является автором (во всяком случае, единоличным) большинства изложенных там идей. Позже фон Нейман построил ещё одну машину, IAS, в которой воплотил архитектурные принципы, изложенные в “сообщении”.

С вычислительной работой, проводившейся для проекта “Манхэттен”, связано много интересных историй; некоторые из них описал другой участник проекта, знаменитый физик Ричард Фейнман, в своей книге “Вы, конечно, шутите, мистер Фейнман” [7]. Там есть, в частности, такой фрагмент:

А что касается мистера Френкеля, который затеял всю эту деятельность, то он начал страдать от компьютерной болезни — о ней сегодня знает каждый, кто работал с компьютерами. Это очень серьёзная болезнь, и работать при ней невозможно. Беда с компьютерами состоит в том, что ты с ними играешь. Они так прекрасны, столько возможностей — если чётное число, делаешь это, если нечётное, делаешь то, и очень скоро на одной-единственной машине можно делать всё более и более изощрённые вещи, если только ты достаточно умён.

Через некоторое время вся система развалилась. Френкель не обращал на неё никакого внимания, он больше никем не руководил. Система действовала очень-очень медленно, а он в это время сидел в комнате, прикидывая, как бы заставить один из табуляторов автоматически печатать арктангенс X. Потом табулятор включался, печатал колонки, потом — бац, бац, бац — вычислял арктангенс автоматически путем интегрирования к составлял всю таблицу за одну операцию.

Абсолютно бесполезное занятие. Ведь у нас уже были таблицы арктангенсов. Но если вы когда-нибудь работали с компьютерами, вы понимаете, что это за болезнь — восхищение от возможности увидеть, как много можно сделать.

К сожалению, наше время слишком сильно отличается от того, когда Фейнман работал в проекте “Манхэттен” и даже от того, когда он писал свою книгу. Далеко не все, кто сейчас имеет дело с компьютерами, знают о существовании этой вот “компьютерной болезни”, компьютеры стали слишком привычным делом, а компьютерные игры большинство людей находит существенно более увлекательным занятием, чем “играть” с самим компьютером, с его возможностями. С другой стороны, Фейнман абсолютно прав в том, что об этой болезни “знал каждый, кто работал с компьютерами” — просто в те времена не существовало “конечных пользователей”, каждый, кто работал с компьютером, был программистом. Как ни странно, именно эта “болезнь” превращает человека в программиста. Если хотите стать программистом — постарайтесь подхватить болезнь, описанную Фейнманом.

Так или иначе, принцип хранимой программы стал однозначным прорывом в области вычислительной техники. До этого машины программировались либо перфолентами, как машины Конрада Цузе, либо вообще перемычками и тумблерами, как ENIAC; на физическое задание программы — перестановку всех перемычек и переключение тумблеров — уходило несколько дней, а затем счёт проходил за час или два, после чего снова предстояло перепрограммировать машину. Программы в те времена не писали, а скорее изобретали, ведь по сути программа была не последовательностью инструкций, а схемой соединения узлов машины.

Хранение программы в памяти в виде инструкций позволило, во-первых, не тратить огромное количество времени на смену программы: её теперь можно было считать с внешнего носителя (перфоленты или колоды перфокарт), разместить в памяти и выполнить, и происходило это достаточно быстро; конечно, на подготовку программы — на то, чтобы её придумать и потом нанести на перфокарты или перфоленты — тоже уходило много времени, но при этом не расходовалось время самой машины, стоившее огромных денег. Во-вторых, использование одной и той же памяти как для кодов команд, так и для обрабатываемых данных позволило трактовать программу как данные и создавать программы, оперирующие другими программами. Такие привычные ныне явления, как компиляторы и операционные системы, были бы немыслимы на машинах, не отвечающих определению машины фон Неймана.

Если говорить точнее, под машиной фон Неймана обычно подразумевают компьютер, обладающий следующими свойствами:

• линейность к однородность памяти: оперативная память состоит из одинаковых ячеек, каждая из которых имеет свой адрес; в простейшем случае в качестве адреса выступает число — номер ячейки;

• произвольный доступ к памяти: центральный процессор может в любой момент времени обмениваться информацией с любой из ячеек памяти, указав её адрес, причём скорость работы никак не зависит от того, к каким именно ячейкам обращается процессор;

• программное управление: машина работает автоматически, выполняя одну за другой команды (инструкции), составляющие программу;

• хранение программы в памяти: программа хранится в ячейках оперативной памяти в виде последовательности числовых кодов отдельных операций;

• неразличимость команд и данных: ячейки памяти, хранящие коды команд программы, физически никак не отличаются от ячеек, хранящих исходные, промежуточные или результирующие данные, с которыми программа должна работать; обязанность помнить, где что лежит, возложена на программиста.

Часто в этот список включают также использование двоичной системы счисления, но этот аспект трудно считать определяющим, он скорее “несколько из другой оперы”.

Между тем объёмы памяти компьютеров успели несколько подрасти; так, уже упоминавшийся IAS Джона фон Неймана имел 512 ячеек памяти по 40 бит каждая. Но пока американцы продолжали в построении компьютеров ориентироваться исключительно на научные и инженерные числовые расчёты, пусть даже и с использованием хранимой программы, в Великобритании в то же самое время нашлись люди, обратившие внимание на потенциал вычислительных машин для обработки информации за пределами узкой “расчётной” области. Первым или во всяком случае одним из первых компьютеров, исходно предназначавшихся для целей более широких, нежели числовые расчёты, считается LEO I, разработанный в британской компании J. Lyons & Со.; примечательно, что эта фирма, занимавшаяся поставками пищевых продуктов, ресторанным и отельным бизнесом, не имела никакого отношения к машиностроительной отрасли. В 1951 году только что построенный компьютер взял на себя изрядную часть функций бухгалтерии и финансового анализа компании, причём собственно вычисления как таковые составляли хотя и заметную, но отнюдь не самую большую долю выполняемых машиной операций. Принимая исходные данные с перфолент и выводя результаты на текстовое печатающее устройство, машина позволила автоматизировать подготовку зарплатных ведомостей и других подобных документов. Пророчество Ады Лавлейс начало потихоньку сбываться: объектом работы для компьютерной программы стала информация, при этом математические расчёты — это важный, но отнюдь не единственный случай её обработки.

Тем временем растущий уровень техники неотвратимо приближал революцию в компьютеростроении. Основным нововведением, обусловившим революцию, стал полупроводниковый транзистор— электронный элемент, который со схемотехнической точки зрения очень похож на радиолампу-триод. Транзистор, как и триод, имеет три контакта, которые обычно называются “базой”, “эмиттером” и “коллектором” (или “затвором”, “истоком” и “стоком” для разновидности транзисторов, называемых полевыми). При изменении напряжения на базе относительно эмиттера (на затворе относительно истока) изменяется ток между эмиттером и коллектором (между истоком и стоком). В аналоговой электронике оба устройства — и лампа-триод, и полупроводниковый транзистор — используются для усиления сигнала за счёт того, что пропускаемые токи между анодом и катодом триода, а равно и между эмиттером и коллектором транзистора могут быть гораздо больше, нежели сигналы, подаваемые для их “закрытия” соответственно на сетку или базу. В цифровых схемах мощности не важны, гораздо важнее эффект управления как таковой. В частности, как и два триода, два транзистора позволяют составить из них триггер, при этом ток, идущий через один транзистор, закрывает второй, и наоборот.

Считается, что первый работающий транзистор был создан в 1947 году в Bell Labs, а в качестве авторов изобретения называют Уильяма Шокли, Джона Бардина и Уолтера Браттейна; спустя несколько лет за это изобретение транзистора им была присуждена Нобелевская премия по физике. Ранние транзисторы были громоздки, ненадёжны и неудобны в работе, однако быстрое совершенствование технологии выращивания кристаллов позволило наладить серийный выпуск транзисторов, которые в сравнении с радиолампами были, во-первых, довольно миниатюрны; во-вторых, для транзисторов не требовался разогрев катода, так что электричества они потребляли тоже гораздо меньше; наконец, опять же в сравнении с лампами, транзисторы были практически безотказны: конечно, они тоже иногда выходят из строя, но это скорее чрезвычайное происшествие, тогда как выход из строя лампы — это просто штатное событие, а сами радиолампы рассматривались скорее как расходный материал, нежели как постоянные узлы конструкции.

Вторым серьёзным изобретением, определившим смену поколений компьютеров, стала память на магнитных сердечниках. Банк такой памяти (рис. 1.2, справа) представлял собой прямоугольную сетку из проводов, в узлах которой располагались ферритовые колечки; каждое колечко хранило один бит информации. В сравнении с громоздким устройством из трёх или четырёх радиоламп, применявшимся для хранения одного бита в ЭВМ первого поколения, это был настоящий прорыв. Компьютеры, построенные на твердотельных электронных компонентах, прежде всего на транзисторах, принято называть компьютерами второго поколения. Если компьютеры первого поколения занимали целые здания, то машина второго поколения умещалась в одной комнате; потребление электроэнергии резко снизилось, а возможности, и прежде всего объём оперативной памяти, существенно возросли. Также возросла надёжность машин, поскольку транзисторы выходят из строя гораздо реже, чем радиолампы. Существенно упала стоимость ЭВМ в денежном выражении. Первые полностью транзисторные вычислительные машины были построены в 1953 году, а уже в 1954 году компания IBM выпустила машину IBM 608 Transistor Calculator, которую называют первым коммерческим компьютером.

Рис. 1.2. Транзистор (слева); банк памяти на ферритовых сердечниках (справа)⁸

Следующий технический прорыв произошел с изобретением интегральных схем — полупроводниковых устройств, в которых на одном кристалле располагается несколько (в современных условиях — до нескольких миллиардов) элементов, таких как транзисторы, диоды, сопротивления и конденсаторы. Компьютеры, построенные на основе интегральных схем, принято относить к третьему поколению; несмотря на всё ещё очень высокую стоимость, эти машины стало возможно выпускать массово — вплоть до десятков тысяч экземпляров. Центральный процессор такого компьютера представлял собой шкафчик или тумбочку, набитую электроникой. По мере совершенствования технологии микросхемы становились всё компактнее, а общее их количество в составе центрального процессора неуклонно снижалось. Наконец в 1971 году произошёл очередной переход количества в качество: были созданы микросхемы, заключающие в себе весь центральный процессор целиком. Какая из микросхем стала первым в истории микропроцессором, доподлинно не известно; чаще всего таковым называют Intel 4004, про который можно, по крайней мере, точно сказать, что это был первый микропроцессор, доступный на рынке. Согласно некоторым источникам, первенство в этом деле следует отдать чипу MP944, который применялся в авионике истребителя F-14, однако широкая публика об этой разработке, как водится, ничего не знала вплоть до 1997 года.

Появление микропроцессоров позволило “упаковать” компьютер в настольный прибор, известный как “персональный компьютер”. С этого момента принято отсчитывать историю четвёртого поколения ЭВМ, каковая продолжается до наших дней⁹.

Как можно заметить, в наше время компьютеры используются для обработки любой информации, которую можно записать и воспроизвести. Кроме традиционных баз данных и текстов, к которым сводилась электронная информатика в середине XX века, компьютеры успешно обрабатывают записанный звук, изображения, видеозаписи; имеются, пусть и в зачаточном состоянии, попытки обрабатывать тактильную информацию — в практическом применении это пока только брайлевские дисплеи для слепых, но инженеры не оставляют попыток создания всевозможных электронных перчаток и прочих подобных устройств. Гораздо хуже обстоят дела со вкусом и запахом, но вкусовая и обонятельная информация вообще на современном уровне техники не поддаётся обработке; можно не сомневаться, что если когда-нибудь будет найден способ записи и воспроизведения вкуса и запаха, компьютеры смогут работать и с этими видами информации.

Конечно, иногда компьютеры используются и для числовых расчётов; существует даже особая индустрия производства так называемых суперкомпьютеров, исходно предназначенных исключительно для решения расчётных задач большого объёма. Современные суперкомпьютеры имеют в своём составе десятки тысяч процессоров и в большинстве случаев производятся в единичных экземплярах; в целом суперкомпьютеры — это скорее исключение из общего правила, тогда как большинство применений компьютеров имеет с численными расчётами весьма мало общего. Естественным образом может возникнуть вопрос — почему же в таком случае компьютеры до сих пор продолжают называться компьютерами? Не лучше ли использовать какой-нибудь другой термин, например, назвать их инфоанализаторами или инфопроцессорами? Как ни странно, это совершенно ни к чему; дело в том, что вычислять можно не только числа и не только по формулам. Если мы припомним понятие математической функции, то немедленно обнаружим, что и область её определения, и область её значений могут быть множествами произвольной природы. Как известно, обрабатывать любую информацию можно лишь при условии, что она представлена в какой-то объективной форме; более того, цифровые компьютеры требуют дискретного представления информации, а это уже не что иное, как представление в форме цепочек символов в некотором алфавите, или попросту текстов; отметим, что именно такое представление произвольной информации рассматривается в теории алгоритмов. При таком подходе любые преобразования информации оказываются функциями из множества текстов во множество текстов, а любая обработка информации становится вычислением функции Получается, что компьютеры по-прежнему занимаются именно вычислениями — пусть и не чисел, а произвольной информации.