Программирование: введение в профессию. 1: Азы программирования - 2016 год
Теперь немного математики - Предварительные сведения
В этой главе мы рассмотрим очень краткие сведения из области математики, без знания и понимания которых в ходе дальнейшего чтения этой книги (и изучения программирования) у вас совершенно однозначно возникнут проблемы. В основном эти сведения относятся к так называемой дискретной математике, которая совершенно игнорируется в школьной программе по математике, но в последние годы вошла в программу школьной информатики. К сожалению, то, как эти вещи обычно излагаются в школе, не оставляет нам иного выбора, кроме как рассказать их самим.
1.5.1. Элементы комбинаторики
Комбинаторикой называется раздел математики, охватывающий задачи вроде “сколькими способами можно...”, “сколько существует различных вариантов...” и прочее в таком духе. В комбинаторике всегда рассматриваются конечные множества, с элементами которых всё время что-то происходит: их переставляют в разном порядке, часть из них отбрасывают, потом возвращают обратно, объединяют в разные группы, сортируют и снова перемешивают и вообще всячески над ними измываются. Мы начнём с одной из самых простых задач комбинаторики, которую, во избежание лишнего занудства, сформулируем языком учебника для младшего школьного возраста.
Вася и Петя решили поиграть в шпионов. Для этого Вася не поленился прикрутить к окошку своей комнаты три цветные лампочки, которые хорошо видно снаружи, если их зажечь, причём зажигать каждую из лампочек можно независимо от других. Вася прикрутил лампочки на совесть, так что менять их местами нельзя. Сколько разных сигналов может передать Вася Пете с помощью своих лампочек, если вариант “ни одна не горит” тоже рассматривать как сигнал?
Вася точно не знает, когда Петя решит посмотреть на его окно, так что всяческие варианты с азбукой Морзе и другими подобными сигнальными системами не подходит: Васе нужно привести лампочки в положение, соответствующее передаваемому сигналу, и в таком виде оставить надолго, чтобы Петя точно успел заметить сигнал.
Многие читатели, возможно, дадут правильный ответ без лишних раздумий: восемь; однако интерес здесь представляет скорее не то, как вычислить ответ (возвести двойку в нужную степень), а то, почему ответ вычисляется именно так. Чтобы выяснить это, мы начнём с тривиального случая: когда лампочка всего одна. Очевидно, что передать здесь можно всего два разных сигнала: один из них будет обозначаться включённой лампочкой, а второй — выключенной.
Добавим теперь ещё одну лампочку. Если, например, эта вторая лампочка будет всё время включена, то можно будет, как и прежде, передать всего два сигнала: “первая лампочка включена” и “первая лампочка выключена”. Но никто не мешает вторую лампочку выключить; в этом положении у нас тоже будет два разных сигнала: “первая включена” и “первая выключена”. Однако тот, кому предназначены сигналы, в нашей задаче Петя, может смотреть на обе лампочки, то есть учитывать состояние их обеих. Первые два сигнала (при включённой второй лампочке) будут отличаться для него от вторых двух сигналов (при выключенной второй лампочке). Всего, следовательно, мы получим возможность передачи четырёх различных сигналов: выключена-выключена, выключена-включена, включена-выключена и включена-включена.
Снабдим эти четыре сигнала номерами от 1 до 4 и добавим ещё одну лампочку, третью. Если её включить, то можно будет передать четыре различных сигнала (с помощью включения и выключения первых двух лампочек). Если её выключить, мы получим ещё четыре сигнала, которые будут отличаться от первых четырёх; всего разных сигналов получится восемь. Останавливаться на этом нас никто не заставляет; пронумеровав имеющиеся восемь сигналов числами от 1 до 8 и добавив четвёртую лампочку, мы получим 8 + 8 = 16 сигналов. Рассуждения можно обобщить: если с помощью n лампочек мы можем передать N сигналов, то добавление лампочки с номером n +1 удваивает количество возможных сигналов (то есть их получается 2N), поскольку первые N у нас получаются с помощью исходно имевшихся лампочек при выключенной новой, а вторые N получается (всё с теми же имевшимися лампочками), если новую включить.
Полезно будет рассмотреть вырожденный случай: ни одной лампочки, то есть n = 0. Конечно, в шпионов так не поиграешь, но случай, тем не менее, с математической точки зрения важный. На вопрос “сколько сигналов можно передать, имея 0 лампочек”, большинство обывателей ответит “нисколько”, но, как ни странно, этот ответ неудачный. В самом деле, наши “сигналы” отличают одну ситуацию от другой, или, точнее, они соответствуют каким-то разным ситуациям. Если говорить ещё точнее, можно заметить, что “ситуаций” на самом деле бесконечно много, просто при передаче сигнала мы игнорируем некоторые факторы, тем самым объединяя множество ситуаций в одну. Например, наш юный шпион Вася мог обозначить сигналом “все лампочки погашены” ситуацию “меня нет дома”; остальные семь комбинаций в сигнализации наших друзей могли бы означать “я делаю уроки”, “я читаю книжку”, “я ем”, “я смотрю телевизор”, “я сплю”, “я занят чем-то ещё” и, наконец, “я ничем не занят, мне вообще нечего делать, так что приходи в гости”. Если внимательно посмотреть на этот список, можно заметить, что в любой из ситуаций возможны дальнейшие уточнения: сигнал “я ем” может одинаково обозначать ситуации “я обедаю”, “я ужинаю”, “я ем вкусный торт”, “я пытаюсь одолеть невкусную и противную перловку” и т. п.; “я делаю уроки” может с равным успехом означать “я решаю задачи по математике”, “я раскрашиваю карты, которые задали по географии” или “я сдуваю упражнения по русскому у соседки Кати”. Возможны варианты “я делаю уроки и хорошо себя чувствую, так что скоро всё сделаю” и “я делаю уроки, но у меня при этом болит живот, так что домашняя работа сегодня затянется”. Каждый из возможных сигналов несколько снижает общую неопределённость, но, разумеется, не устраняет её.
Вернёмся к нашему вырожденному примеру. Не имея ни одной лампочки, мы вообще не можем отличать ситуации друг от друга, но значит ли это, что у нас нет вообще никаких ситуаций? Очевидно, что это не так: наши юные шпионы по-прежнему чем-то заняты или, наоборот, не заняты, просто наш вырожденный вариант сигнализации не позволяет эти ситуации различать. Попросту говоря, мы объединили все возможные ситуации в одну, полностью убрав какую-либо определённость; но ведь мы объединили их в одну ситуацию, а не в ноль таковых.
Теперь уже всё становится на свои места: при нуле лампочек у нас один возможный сигнал, а добавление каждой новой лампочки увеличивает количество сигналов вдвое, так что N = 2n, где n— количество лампочек, а N — количество возможных сигналов. Попутно отметим, что иногда приведённые рассуждения позволяют лучше понять, почему считается, что ![]() для любого k > 0.
для любого k > 0.
Задача про количество сигналов, передаваемых с помощью п лампочек, каждая из которых может гореть или не гореть, эквивалентна многим другим задачам; прежде чем мы перейдём к сухой математической сути, приведём ещё одну формулировку:
У Маши есть брошка, цепочка, серёжки, колечко и браслет. Каждый раз, выходя из дома, Маша долго раздумывает, какие из украшений в этот раз надеть, а какие оставить дома. Сколько у неё есть вариантов выбора?
Чтобы понять, что это та же самая задача, давайте введём произвольное допущение, не относящееся к сути задачи и никак эту суть не затрагивающее: пусть наш юный шпион Вася из предыдущей задачи оказался младшим братом Маши и решил от нечего делать сообщать своему приятелю Пете, какие из украшений его сестра нацепила в этот раз. Для этого ему придётся добавить к трём уже имеющимся ещё две лампочки, чтобы их стало столько же, сколько у Маши украшений. Первая лампочка из пяти будет обозначать, надела ли Маша брошку, вторая — надела ли Маша цепочку, и так далее, по одной лампочке на каждое украшение из имеющихся у Маши. Мы уже знаем, что количество сигналов, передаваемых пятью лампочками, равно 25 = 32; очевидно, что это количество в точности равно количеству комбинаций из украшений, которые надела Маша.
На “высушенном” математическом языке та же самая задача, полностью лишённая “шелухи”, не влияющей на результат, и сведённая к чистым абстракциям, существенным с точки зрения решения, формулируется так:
Дано множество из n элементов. Сколько существует различных подмножеств этого множества?
Ответ 2n несложно запомнить, и, к сожалению, в школе обычно именно так и делают; результатом такого “дешёвого и сердитого” подхода к изучению математики становится лёгкость, с которой ученика можно совершенно запутать сколько-нибудь нестандартными формулировками условий задачи. Вот вам пример:
У Димы есть четыре разноцветных кубика. Ставя их один на другой, Дима строит “башни”, причём один кубик, на котором ничего не стоит, Дима тоже считает “башней”; иначе говоря, башня у Димы имеет высоту от 1 до 4 кубиков. Сколько различных “башен” можно построить из имеющихся кубиков, по одной за раз?
Кабы вы только знали, уважаемый читатель, сколько старшеклассников, совершенно не задумываясь, выдают на эту задачу ответ 24! Между прочим, некоторые из них, заметив, что пустая башня условиями задачи исключена, “совершенствуют” свой ответ, вычтя “запрещённый” вариант, и получают 24 — 1. Правильнее он от этого не становится ни на йоту, потому что это попросту совершенно не та задача, в которой двойку возводят в степень n; но чтобы это понять, необходимо для начала понимать, почему двойку возводят в степень n в “той” задаче, а вот с этим у школьников, зазубривших “магическое” 2n, обнаруживаются фатальные проблемы.
Кстати, правильный ответ этой задачи — 64, но решение не имеет ничего общего с возведением двойки в шестую степень; если бы кубиков было три, ответ был бы 15, а для пяти кубиков правильный ответ будет 325. Всё дело тут, разумеется, в том, что в этой задаче важно не только из каких кубиков состоит башня, но и в каком порядке расположены кубики, составляющие башню. Поскольку для башен, состоящих более чем из одного кубика, можно получать разные варианты, просто меняя кубики местами, итоговых комбинаций оказывается гораздо больше, чем если бы мы рассматривали возможные наборы кубиков без учёта их порядка.
Прежде чем перейти к рассмотрению задач, в которых существенны перестановки, рассмотрим ещё пару задач на количество вариантов без перестановок элементов. Первую из них мы “состряпаем” из исходной задачи про юных шпионов:
Папа принёс Васе дешёвый китайский светильник, который может либо быть выключен, либо просто светиться, либо мигать. Вася немедленно прикрутил светильник к своему окну, где уже есть три обычные лампочки. Сколько разных сигналов Вася может передать Пете теперь, после усовершенствования своего шпионского оборудования?
Задача, конечно, совершенно элементарная, но она представляет интерес вот в каком плане. Если человек понимает, как (и почему именно так) решается задача с тремя обыкновенными лампочками, то никаких проблем с “заковыристой” лампочкой, имеющей три разных состояния, у него не возникнет; но если задачу пытается решать среднестатистический школьник, которому на уроке вдолбили формулу N = 2n, не объяснив, откуда она взялась, то с хорошей степенью достоверности на этой новой задаче он “сядет”. А ведь решается она ничуть не сложнее, чем предыдущая, причём ровно теми же рассуждениями: мы можем передать восемь разных сигналов, если китайский светильник погашен; столько же мы можем передать, если он включён; и ещё столько же — если он мигает. Итого 8 + 8 + 8 = 3 ∙ 8 = 24. Этот случай показывает, насколько схема вывода формулы ценнее самой формулы, и сейчас самое время отметить, что в комбинаторике всегда так; больше того, комбинаторные формулы попросту вредно помнить, их лучше каждый раз выводить, благо все они настолько простые, что вывести их можно в уме. Запомнив любую формулу из области комбинаторики, вы рискуете применить её не по делу, как это делают вышеупомянутые школьники, пытаясь решать задачу про башни из кубиков.
Ещё одна задача на ту же тему выглядит так:
У Оли есть заготовки для флажков в форме обыкновенного прямоугольника, треугольника и прямоугольника с вырезом; ещё у Оли есть нашивки другого цвета в форме кружочка, квадратика, треугольничка и звёздочки. Оля решила сделать много флажков для праздника; сколько различных флажков она может сделать, пришивая к одной из имеющихся заготовок одну из имеющихся нашивок?
Эта задача тоже, можно сказать, стандартно-хрестоматийная, так что большинство людей, хотя бы приблизительно знающих, о чём идёт речь, просто перемножат два числа и получат совершенно правильный ответ — 12. Но гораздо интереснее здесь не то, как решить конкретную задачу, а то, какими вообще путями можно это сделать. Для начала отметим, что наше рассуждение с лампочками замечательно проходит и здесь: в самом деле, если бы у Оли были только заготовки прямоугольной формы, то она смогла бы сделать столько разных флажков, сколько у неё есть разных нашивок, то есть четыре. Если бы у неё были только заготовки треугольной формы, она бы тоже смогла сделать четыре разных флажка, и то же самое — если бы все её заготовки имели форму прямоугольника с вырезом. Но ведь первые четыре варианта отличаются от вторых четырёх вариантов, а третьи четыре варианта отличаются и от первых, и от вторых — формой заготовки; следовательно, всего вариантов 3 ∙ 4 = 12.
Однако больший интерес может представлять другой вариант рассуждений. Составим таблицу, в которой будет три столбца по числу разных заготовок и четыре строки по числу разных нашивок. В каждом столбце расположим флажки, сделанные с использованием соответствующей заготовки, а в каждой строке — флажки, сделанные с использованием соответствующей нашивки (см. рис. 1.7). Для каждого, у кого в мозгах сформирована абстракция умножения, немедленно становится очевидно, что клеток с флажками получилось 3 ∙ 4 = 12; интересно, что это понимание сродни понятию площади прямоугольника, только для дискретного случая.
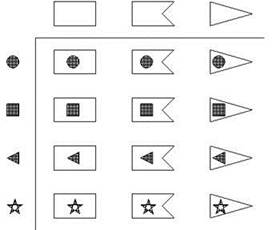
Рис. 1.7. Задача о флажках
Наконец, рассмотрим ещё одну задачу, похожую на ту, решение которой мы оставили на потом:
У Димы есть ящик с кубиками четырёх разных цветов. Ставя кубики один на другой, Дима строит “башни”, причём один кубик, на котором ничего не стоит, Дима тоже считает “башней”; иначе говоря, башня у Димы имеет высоту от 1 до 4 кубиков. Сколько различных “башен” можно построить из имеющихся кубиков? Считается, что кубиков каждого цвета у Димы имеется сколько угодно.
Несмотря на кажущуюся схожесть (здесь совпадают примерно три четверти текста), эта задача гораздо проще своей предыдущей версии, где кубиков было всего четыре. Впрочем, опять-таки, если не понимать, как получаются комбинаторные результаты, эту задачу решить невозможно, поскольку стандартные формулы для неё не срабатывают. Правильный ответ здесь — 340; предлагаем читателю самостоятельно продемонстрировать, как этот ответ получился.
Пока все задачи, которые мы рассматривали, решались без учёта перестановок; единственную задачу, в которой перестановки оказались существенны, мы решать не стали. Разговор о задачах с перестановками мы начнём, собственно говоря, с канонической задачи о количестве возможных перестановок. Как обычно, для начала сформулируем её по-школьному:
У Коли в мешке лежат семь шариков для американского бильярда с разными номерами (например, “сплошные” от единички до семёрки). Сколькими разными способами Коля может поставить их на полке в ряд?
Прийти к правильному ответу можно двумя способами, и мы рассмотрим их оба. Начнём с тривиального варианта: есть всего один шарик, сколькими “способами” можно поставить его на полку? Очевидно, что способ тут только один. Возьмём теперь два шарика; в принципе, неважно, какие у них номера, результат от этого не меняется, но пусть для определённости это будут шарики с номерами 2 и 6. Очевидно, есть два способа расставить их на полке: “двойка слева, шестёрка справа” и “шестёрка слева, двойка справа”. Первый способ назовём прямым, второй — обратным, поскольку номера шаров слева направо в этом случае не возрастают, а, наоборот, убывают.
Добавим теперь третий шарик (например, пусть это будет номер 3) и посмотрим, сколько стало способов. Крайний левый шарик мы можем выбрать тремя способами: поставить слева двойку, поставить слева тройку или поставить слева шестёрку. Какой бы шарик мы ни выбрали, оставшиеся два шарика на оставшиеся две позиции можно поставить двумя уже известными нам способами — прямым и обратным; иначе говоря, на каждый вариант выбора крайнего левого шарика имеются два варианта расстановки остальных, то есть всего вариантов будет шесть (рис. 1.8). Отметим, что обычно перестановки нумеруют именно в таком порядке: сначала их сортируют по возрастанию первого элемента (то есть сначала идут перестановки, в которых первый элемент имеет наименьший номер, а в конце — перестановки, где номер первого элемента наибольший), затем все перестановки, имеющие одинаковый первый элемент, сортируют по возрастанию второго, и так далее.
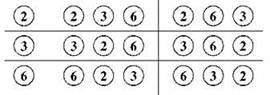
Рис. 1.8. Перестановки трёх шариков
Если теперь добавить четвёртый шарик (пусть это будет шар с номером 5), мы получим четыре способа выбора крайнего левого из них, и при каждом таком способе остальные шарики можно будет расставить уже известными нам шестью способами; всего перестановок для четырёх шариков получится, соответственно, 24. Теперь мы, можно надеяться, готовы к обобщению: если для k — 1 шаров существует Мk-1 возможных перестановок, то, добавляя k-й шар, мы количество перестановок увеличим в к раз, то есть Мk = k ∙ Мk-1. В самом деле, при добавлении k-го шаравсего шаров становится как раз k, то есть самый первый (например, крайний левый) шар мы можем выбрать к способами, а остальные, согласно сделанному предположению, можно расставить (при фиксированном крайнем левом) Мk-1 способами. Поскольку начали мы с того, что для одного шара существует одна возможная перестановка, то есть М1 = 1, общее число перестановок для к шаров получится равным произведению всех натуральных чисел от 1 до k:
![]()
Как известно, это число называется факториаломk и обозначается “k!”; на самом деле определением факториала натурального числа k считается “число перестановок из k элементов”, а то, что факториал равен произведению чисел от 1 до k — это следствие.
Для сформулированной выше задачи ответ составит, таким образом, 7! = 5040 комбинаций.
К этому результату можно прийти и другим путём. Рассмотрим мешок, в котором лежат семь шаров, и семь пустых позиций на полке. Выбрать шар для заполнения первой пустой позиции мы можем семью способами; какой бы шар мы ни выбрали, в мешке их останется шесть. Иначе говоря, когда одна позиция уже заполнена, для заполнения второй позиции у нас имеется шесть вариантов, вне зависимости от того, каким из семи возможных способов была заполнена первая пустая позиция. Таким образом, на каждый из семи способов заполнения первой позиции у нас есть шесть способов заполнения второй позиции, а всего способов заполнения первых двух позиций получается 7 ∙ 6 = 42. В мешке при этом остаётся пять шаров, то есть на каждую из 42 комбинаций первых двух шаров есть пять вариантов выбора третьего шара; всего вариантов для первых трёх шаров получается 42 ∙ 5 = 210. Но на каждую такую комбинацию у нас естьчетыре способа выбора очередного шара, ведь в мешке их осталось четыре; и так далее. Предпоследний шар из оставшихся в мешке мы сможем выбрать двумя способами, последний — одним. Получаем, что всего вариантов расстановки семи шаров у нас
![]()
Повторив это же рассуждение для случая k шаров, мы придём к уже знакомому нам выражению
![]()
только в этот раз мы к нему пришли, двигаясь от больших чисел к меньшим, а не наоборот, как в предыдущем рассуждении. Отметим, что для понимания дальнейших выкладок нам будут полезны оба рассуждения.
Рассмотрим теперь промежуточную задачу, начав, как обычно, с частного случая:
У КОЛИ В мешке по-прежнему лежат семь шариков для американского бильярда с номерами от единички до семёрки.
Вася показал Коле небольшую полочку, на которой могут поместиться только три шара. Сколькими разными способами Коля может заполнить эту полочку шарами?
Несомненно, читатель без труда найдёт ответ на этот вопрос, повторив три первых шага из приведённого выше рассуждения: первый из трёх шаров мы можем выбрать семью способами, второй — шестью, третий — пятью; ответ составит 7∙6∙5 = 210 вариантов. Это число можно записать, используя символ факториала:
![]()
В общем случае, когда у нас есть п предметов (элементов множества) и нужно составить упорядоченный набор (кортеж) длиной k, имеем:
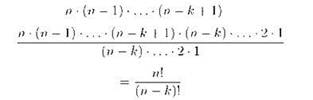
Эту величину, называемую количеством размещений из n по k, иногда в русскоязычной литературе обозначают Ank (читается А из эн по ка). В англоязычной литературе, а также и в некоторых русскоязычных источниках используется обозначение (n)k, которое называют убывающим факториалом.
Сейчас, пожалуй, самое время решить задачу, которую мы сформулировали на стр. 109, но не стали решать. Напомним её условие:
У Димы есть четыре разноцветных кубика. Ставя их один на другой, Дима строит башни, причём один кубик, на котором ничего не стоит, Дима тоже считает башней; иначе говоря, башня у Димы имеет высоту от 1 до 4 кубиков. Сколько различных башен можно построить из имеющихся кубиков?
Ясно, что башен из четырёх кубиков будет 4! = 24. Башен из трёх кубиков получится столько же: каждая из них получается из одной строго определённой башни высоты 4 снятием одного кубика, но то, что этот кубик Дима то ли держит в руках, то ли куда-то убрал, вместо того чтобы поставить его на вершину башни, никак не изменяет количества комбинаций. Наконец, башен из двух кубиков будет 4 ∙ 3 = 12, а башен из одного кубика — 4, по числу имеющихся кубиков. 24 + 24 + 12 + 4 = 64, это и есть ответ задачи.
Теперь мы подошли вплотную к очередной классической задаче, ради которой, в общем и целом, и был затеян весь разговор о перестановках. Как обычно, мы начнём с частного случая:
У Коли в мешке лежат всё те же семь шариков для американского бильярда с номерами от единички до семёрки. Вася дал Коле пустой мешок и попросил переложить в него три любых шара. Сколькими разными способами Коля может выполнить просьбу Васи?
Эта задача отличается от предыдущей задачи про Колю и Васю тем, что шары в мешке, очевидно, перемешаются; иначе говоря, нас больше не интересует порядок следования элементов в итоговых комбинациях. Чтобы понять, как эта задача решается, представим себе, что Колю тоже заинтересовало, сколькими же способами он может выбрать три шара из имеющихся семи без учёта порядка, и он для начала выписал на листе бумаги все 210 вариантов, полученных при решении предыдущей задачи, где вместо мешка была полочка, то есть все возможные варианты размещений из семи по три с учётом порядка элементов. Зная, что варианты, различающиеся только порядком следования элементов, придётся теперь рассматривать как одинаковые, Коля решил для пробы посмотреть, сколько раз среди 210 выписанных комбинаций встречаются комбинации, состоящие из шаров с номерами 1, 2 и 3. Внимательно просмотрев свои записи, Коля обнаружил шесть таких комбинаций: 123, 132, 213, 231, 312 и 321. Решив проверить какой-нибудь другой набор шаров, Коля просмотрел свой список в поисках комбинаций, использующих шары с номерами 2, 3 и 6; таких комбинаций тоже нашлось шесть: 236, 263, 326, 362, 623 и 632 (эти комбинации уже знакомы нам по рис. 1.8).
На этом месте своих изысканий Коля стал (будем надеяться, что вместе с нами) догадываться, что то же самое получится для любого набора шариков. В самом деле, ведь список из 210 комбинаций включает все возможные варианты выбора по три шара из семи с учётом их порядка; как следствие, какие бы мы ни взяли три шара из семи, в нашем списке найдутся, опять-таки, все комбинации, состоящие из этих трёх шаров, то есть, попросту, все перестановки выбранных трёх шаров; ну а перестановок из трёх элементов, как мы знаем, существует 3! = 3∙2∙1 = 6. Получается, что любая из интересующих нас комбинаций представлена в списке шесть раз; иначе говоря, список ровно вшестеро длиннее, чем нужный нам результат. Нам осталось лишь поделить 210 на 6, и мы получим ответ задачи: ![]()
В общем случае нас интересует, сколькими способами можно выбрать k предметов из имеющихся n без учёта их порядка; соответствующая величина называется количеством сочетаний из n по k и обозначается как Cnk (читается “Це из эн по ка”; буква С происходит от слова combinations, то есть “комбинации”, или “сочетания”). Повторяя вышеприведённые рассуждения для общего случая, заметим, что, если рассмотреть все (n)k размещений (которые отличаются от сочетаний тем, что в них порядок элементов считается важным), то в нём каждое сочетание будет представлено k! раз по числу возможных перестановок к элементов, т. е. число ![]() превосходит искомое Cnk ровно в k! раз. Собственно говоря, всё, осталось только поделить
превосходит искомое Cnk ровно в k! раз. Собственно говоря, всё, осталось только поделить ![]() на k!, и мы получим самую главную формулу школьной комбинаторики:
на k!, и мы получим самую главную формулу школьной комбинаторики:
![]()
А теперь мы скажем вам то, что вам вряд ли могли говорить в школе: ни в коем случае, ни за какие пряники, ни при каких условиях не запоминайте эту формулу! Если вы всё-таки случайно запомните её или если вы успели заучить эту формулу наизусть до того, как вам в руки попалась наша книга, постарайтесь её снова забыть, как самый страшный ночной кошмар. Дело в том, что помнить эту формулу просто опасно: возникает соблазн применить её без лишних раздумий в любой комбинаторной задаче, где присутствуют какие-нибудь два числа; в большинстве случаев такое применение будет ошибочным и даст неверные результаты.
Вместо запоминания самой формулы запомните лучше схему её вывода. Когда вам действительно будет нужно найти число сочетаний из n исходных элементов по k выбираемых элементов, вы сможете вывести формулу для Cnk в уме за то время, пока будете её писать; для этого, написав “Cnk =” и нарисовав дробную черту, прокрутите в уме примерно следующее: общее число перестановок из n составляет n!, но нам нужны только к из них, так что лишние члены факториала мы убираем, поделив на (n — k)!; то, что получилось, есть количество комбинаций с учётом порядка, а нас порядок не волнует, так что получается, что мы каждую комбинацию посчитали k! раз, делим на k! и получаем то, что нам нужно. Такой подход не позволит применить формулу не по делу, потому что вы будете знать точно, что эта формула означает и для чего её можно применять.
Интересно, что ту же самую формулу можно вывести и другим рассуждением. Представьте себе, что мы сначала выставили на полку в ряд п шаров, потом отделили первые к из них и ссыпали в мешок, а остальные n — k ссыпали в другой мешок; естественно, в каждом мешке шары перемешались. Сколько возможно таких (итоговых) комбинаций, в которых шары разложены по двум мешкам, причём порядок ссыпания шаров в каждый из мешков нас не волнует? Пойдём по уже знакомой нам схеме рассуждений: изначально у нас было n! комбинаций, но среди них каждые k! стали неразличимы из-за того, что k шаров перемешались в первом мешке, так что осталось ![]() комбинаций (после того, как первые к шаров ссыпали в первый мешок и там перемешали, а остальные (n — k) шаров пока никуда не ссыпали), но среди этих комбинаций каждые (n — k)! потом тоже стали неразличимы из-за перемешивания шаров во втором мешке. Итого n! превосходит искомое Сnk в k!(n — k)! раз, то есть
комбинаций (после того, как первые к шаров ссыпали в первый мешок и там перемешали, а остальные (n — k) шаров пока никуда не ссыпали), но среди этих комбинаций каждые (n — k)! потом тоже стали неразличимы из-за перемешивания шаров во втором мешке. Итого n! превосходит искомое Сnk в k!(n — k)! раз, то есть ![]()
Это рассуждение примечательно тем, что оно, в отличие от предыдущего, симметрично: оба множителя в знаменателе дроби получаются одинаковым путём. Задача и в самом деле обладает некоторой симметрией: выбрать, какие k шаров пересыпать в другой мешок, можно, очевидно, тем же числом способов, как и выбрать, какие k шаров оставить в мешке. Это выражается тождеством Сnk ≡ Сnn-k.
Для вырожденных случаев делают допущение, что Сn0 = Сnn = 1 для любого натурального n, но это допущение, как нетрудно убедиться, вполне естественно. В самом деле, Сn0 соответствует ответу на вопрос “сколькими способами можно ноль шаров из n имеющихся пересыпать в другой мешок”. Очевидно, такой способ один: мы просто ничего не делаем, и все шары остаются лежать в исходном мешке, а второй мешок так и остаётся пустым. Практически так же обстоят дела и с Сnn: “сколькими способами можно n шаров из мешка с n шарами пересыпать в другой мешок”? Естественно, ровно одним: подставляем второй мешок, пересыпаем в него всё, что нашлось в первом, и дело сделано.
Числа Сnk называют биномиальными коэффициентами, потому что через них можно записать общий вид разложения бинома Ньютона:
![]()
Например, (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5, при этом числа 1, 5,10,10, 5 к 1 представляют собой С50, С51, С52, С53, С54 и С55. Интересно, что большинство профессиональных математиков полагают здесь всё настолько очевидным, что ни до каких объяснений не снисходят; между тем, остальная публика, в том числе и большинство людей, имеющих высшее техническое образование, но не являющихся профессиональными математиками, вообще не видят связи между задачей о пересыпании шаров из мешка в мешок и разложением бинома Ньютона; на вопрос, откуда в формуле бинома взялись комбинации шаров, они обычно отвечают сакраментальным “так получилось”, видимо, полагая происходящее то ли случайным совпадением (хотя откуда в математике случайности?), то ли взаимосвязью настолько нетривиальной, что её вообще невозможно проследить.
Между тем, чтобы получить в процессе разложения бинома нашу “задачу о мешках с шарами”, достаточно заметить, что речь должна идти не о том, как разложить бином на слагаемые (это вопрос слишком общий к затрагивает отнюдь не только комбинации), а о том, какой коэффициент будет стоять при каждом члене разложения.
Как известно, если при раскрытии скобок не приводить однородные члены, то в итоговой сумме получится 2n слагаемых. Например:
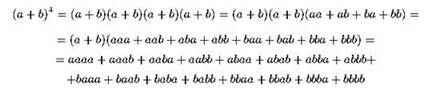
Для большей наглядности мы здесь не стали использовать показатели степени. Каждое слагаемое итогового разложения представляет собой произведение, в котором из каждой исходной “скобки” взято либо а, либо б, а сама сумма состоит из всех возможных таких слагаемых. Нетрудно видеть, что их возможно ровно 2n, ведь из каждой скобки мы должны взять либо а, либо б, то есть мы получаем уже знакомую нам задачу про юных шпионов к лампочки; но к делу это в данном случае не относится.
После приведения подобных членов мы, очевидно, получим сумму одночленов вида Makbn-k (напомним, что в нашем примере разложения n = 4, но это лишь частная иллюстрация к общим рассуждениям), и нам осталось выяснить, чему равно М; нетрудно догадаться, что М представляет собой ответ на вопрос, сколькими способами можно из всех n ““скобок” выбрать к ““скобок”, из которых мы возьмём сомножителем слагаемое а, а из остальных возьмём слагаемое b. В такой формулировке уже становится понятно, что это и есть, собственно говоря, наша задача про шары: вместо шаров у нас “скобки”; вместо перекладывания шара в другой мешок мы выбираем из “скобки” слагаемое b, вместо оставления шара в исходном мешке мы выбираем из “скобки” слагаемое а. В частности, для нашего примера одночлен a2b2 встречается в разложении шесть раз:
![]()
что соответствует значению С24; после приведения подобных членов в итоговом многочлене появится одночлен 6а2b2. В то же время, например, одночлен b4 встретился нам всего один раз (в виде bbbb), что соответствует С44 = 1, и так далее.
Известен очень простой способ вычисления значений Сnk, не требующий никаких операций кроме сложения — так называемый треугольник Паскаля (рис. 1.9). Первая строчка этого “треугольника” состоит из одной единицы, которая соответствует значению С00 (сколькими способами можно из пустого мешка в другой пустой мешок пересыпать ноль шариков? Очевидно, одним). Последующие строки начинаются к заканчиваются единицей, что соответствует Сn0 и Сnn; все остальные элементы строк получаются сложением элементов предыдущей строки, между которыми стоит вычисляемый элемент. Например, двойка в середине третьей строки получена как сумма стоящих над ней единичек; две тройки в следующей строке получены сложением стоящих над каждой из них двойки и единицы; в нижней из показанных строк число 15 получено сложением стоящих над ним 5 и 10, и так далее. Треугольник Паскаля основан на тождестве ![]() которое очень легко вывести сугубо аналитически:
которое очень легко вывести сугубо аналитически:
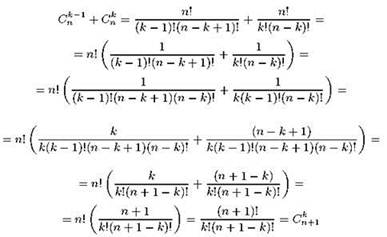
Однако гораздо интереснее в контексте нашего разговора “комбинаторный смысл” этого тождества, который оказывается неожиданно простым. Итак, пусть у нас был мешок с те шарами, пронумерованными от 1 до n. Нам дали ещё один шар, снабжённый номером n + 1, и спросили, сколькими способами мы сможем теперь, когда у нас есть дополнительный шарик, насыпать fcшаров в пустой мешок. Держа (n + 1)-й шар в руках, мы сообразили, что все наши варианты можно разделить на две непересекающиеся группы. Первая группа вариантов основывается на том, что мы так и продолжаем держать в руках (n + 1)-й шар, или вообще прячем его в карман, а для пересыпания в пустой мешок используем только шары, которые у нас были изначально. Таких вариантов, как несложно догадаться, Сnk. Вторая группа вариантов предполагает, наоборот, что мы для начала кидаем в пустой мешок наш (n + 1)-й шар, и нам остаётся досыпать туда (k — 1) шаров из нашего исходного мешка; это можно сделать Сnk-1 способами. Общее количество вариантов, таким образом, получается Сnk + Сnk-1, что и требовалось доказать.
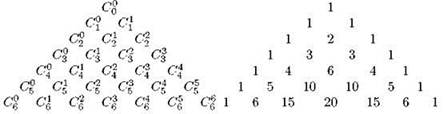
Рис. 1.9. Треугольник Паскаля
Треугольник Паскаля обладает множеством интересных свойств, перечислять которые мы здесь не станем, поскольку и так уже несколько увлеклись. Отметим только одно из них: сумма чисел в любой строке треугольника Паскаля представляет собой 2n, где n — номер строки, если их нумеровать с нуля (то есть n соответствует степени бинома, коэффициенты разложения которого составляют данную строку). Иначе говоря, ![]() Это свойство тоже имеет совершенно тривиальный комбинаторный смысл, который мы предлагаем читателю найти самостоятельно в качестве упражнения.
Это свойство тоже имеет совершенно тривиальный комбинаторный смысл, который мы предлагаем читателю найти самостоятельно в качестве упражнения.
В заключение разговора о комбинаторике рассмотрим ещё одну хрестоматийную задачу:
В турнире по шахматам участвует семь шахматистов, причём предполагается, что каждый с каждым сыграет ровно одну партию. Сколько всего будет сыграно партий?
Ясно, что каждый из семерых должен сыграть шесть партий, по одной с каждым из остальных участников турнира. Но вот следующая фраза почему-то многих начинающих комбинаторов вгоняет в ступор: поскольку в каждой партии участвуют двое, всего партий будет вдвое меньше, чем 7 ∙ 6, т. е. всего будет сыграна ![]()
Поскольку именно с этим вот “в каждой партии участвуют двое” имеются сложности, придётся дать некоторые пояснения, и мы дадим их двумя способами. Для начала давайте припомним, что шахматисты на соревнованиях обязательно записывают все ходы, причём это делают оба участника каждой игры; заполненные протоколы потом сдаются судьям. Представьте себе теперь, что каждый из участников турнира заготовил по одному бланку протокола для каждой предстоящей ему партии. Ясно, что таких бланков каждый заготовил шесть, а всего, стало быть, их было заготовлено 6 ∙ 7 = 42. Теперь шахматисты встретились в зале в день турнира и начали играть; после каждой партии её участники сдают свои протоколы судьям, то есть после каждой партии судьи получают два протокола. В конце турнира, очевидно, все 42 протокола оказываются у судей, но ведь судьи получали по два протокола после каждой партии — следовательно, всего партий было вдвое меньше, то есть 21.
Есть и второй вариант объяснения. Результаты спортивных соревнований по так называемой “круговой системе”, где каждый играет с каждым ровно одну партию, обычно представляют в виде турнирной таблицы, причём для каждого участника турнира предусматривается своя строка и свой столбец. Диагональные клетки таблицы, то есть такие, которые стоят на пересечении строки и столбца, соответствующих одному игроку, заштрихованы, поскольку сам с собой никто играть не собирается. Далее, если, например, игрок Б с игроком Д сыграли партию, и Б выиграл, то считается, что партия закончилась со счётом 1:0 в пользу Б; в его строку на пересечении со столбцом Д заносится результат “1:0”, тогда как в строку Д на пересечении со столбцом Б заносится результат “0:1” (см. рис. 1.10).
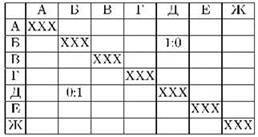
Рис. 1.10. Турнирная таблица
Очевидно, что сначала клеток в таблице было 7 ∙ 7 = 49, но семь из них сразу же закрасили, и их осталось 42; по итогам каждой партии заполняются ещё две клетки, то есть после 21 партии все клетки окажутся заполнены, а турнир окончится.
Будучи переведённой на сугубо математический язык, эта задача превращается в задачу о количестве рёбер в полном графе. Напомним, что граф — это некое конечное множество абстрактных вершин, а также конечный набор неупорядоченных пар вершин, которые называются рёбрами; граф изображают в виде рисунка, на котором вершины обозначаются точками, а рёбра — линиями, соединяющими соответствующие вершины. Полным графом называется такой граф, в котором любые две вершины соединены ребром, притом только одним. Полный граф, имеющий nвершин, имеет ![]() ребер; в самом деле, в каждую вершину входит (n — 1) ребро, то есть всего в графе n(n — 1) “концов рёбер”, но поскольку каждое ребро имеет два конца, их общее число составляет
ребер; в самом деле, в каждую вершину входит (n — 1) ребро, то есть всего в графе n(n — 1) “концов рёбер”, но поскольку каждое ребро имеет два конца, их общее число составляет ![]() .
.
1.5.2. Позиционные системы счисления
Как известно, общепринятая и знакомая нам с дошкольного возраста система записи чисел арабскими цифрами представляет собой частный случай позиционной системы счисления. Мы используем всего десять цифр; при этом, если число просматривать справа налево, то каждая следующая цифра имеет “вес” в десять раз больший, чем предыдущая, то есть действительное значение цифры зависит от её позиции в записи числа (именно поэтому система называется позиционной). Это никоим образом не совпадение: если мы хотим, чтобы каждое целое число могло быть записано в нашей системе, и притом только одним способом, то каждая следующая цифра должна “весить” ровно во столько же раз больше, сколько мы используем цифр. Число, обозначающее одновременно количество используемых цифр и то, во сколько раз каждая следующая цифра “тяжелее” предыдущей, называется основанием системы счисления; для десятичной системы основанием служит, как несложно догадаться, число десять.
Здесь имеется довольно простая связь с комбинаторикой, которую мы рассматривали в предыдущем параграфе. В самом деле, пусть у нас имеется к пронумерованных флагштоков к неограниченное количество флажков n — 1 разных расцветок, то есть на каждом из к флагштоков мы можем поднять любой из n — 1 флажков, либо оставить флагшток пустым, и всё это независимо друг от друга; иначе говоря, каждый из к флагштоков независимо находится в одном из n состояний. Тогда общее число комбинаций флажков составит nk. Если по какой-то причине нам этого количества комбинаций не хватит, придётся добавить ещё один флагшток; причём можно, в принципе, считать, что их изначально есть “сколько угодно”, просто все, кроме к первых, пустые.
Ровно это и происходит при записи чисел с помощью позиционной системы счисления. Мы используем n цифр, причём цифра 0 соответствует “пустому флагштоку”; при работе с k разрядами (позициями) это даёт нам nk чисел, от 0 до nk — 1. Например, существует 1000 = 103 трёхзначных десятичных чисел — от 0 до 999. При этом мы изначально можем предполагать, что разрядов вообще-то бесконечное количество, просто все они, кроме первых (младших) к, содержат нули.
При прибавлении единицы к числу nk — 1 (в нашем примере — к числу 999) мы исчерпываем возможности к разрядов и вынуждены задействовать ещё один разряд, (k + 1)-й. Раньше этого момента задействовать новый разряд не имеет смысла, ведь мы можем представить все меньшие числа, используя всего к разрядов, и если при этом “залезть” в следующий разряд, мы получим больше одного представления для одного и того же числа. С другой стороны, если возможности комбинаций младших разрядов уже исчерпаны, нам не остаётся иных возможностей, кроме задействования следующего разряда. Логично в этом следующем разряде начать с наименьшей возможной цифры, то есть с единицы, а все младшие разряды обнулить, чтобы “начать сначала”; таким образом, единица k + 1 разряда обязана соответствовать общему количеству комбинаций, которые можно получить в первых к разрядах.
То, что всё человечество сейчас использует именно систему по основанию 10, есть не более чем случайность: основание системы счисления соответствует количеству пальцев у нас на руках. Работа именно с этой системой кажется нам “простой” и “естественной” лишь только потому, что мы привыкаем к ней с раннего детства; на самом деле, как мы позже увидим, считать в двоичной системе гораздо проще, там не нужна таблица умножения (вообще; то есть её там просто нет), а само умножение в столбик, столь ненавистное школьникам младших классов, в двоичной системе превращается в тривиальную процедуру “выписываний со сдвигами”. Ещё в XVII веке Готфрид Вильгельм Лейбниц, впервые в истории описавший двоичную систему счисления в том виде, в котором она известна сейчас, заметил это обстоятельство и заявил, что использование десятичной системы — это роковая ошибка человечества.
Так или иначе, мы можем при желании использовать любое количество цифр, начиная от двух, для создания позиционной системы счисления; если при этом следовать традиционному подходу и, используя n цифр, приписывать им значения от 0 до (n — 1), то35 с такой системой записи чисел можно будет работать во многом по аналогии с хорошо знакомой нам десятичной системой. Например, в любой системе счисления запись числа 1000n (где n — основание системы счисления) будет означать n3: в десятичной системе это тысяча, в двоичной — 8, в пятеричной — 125. Необходимо только помнить одну важную вещь. Система счисления определяет, как будет записано число, но само число и его свойства никак от системы счисления не зависят; простое число всегда останется простым, чётное — чётным, 5 ∙ 7 будет 35 вне всякой зависимости от того, какими цифрами (да хоть римскими!) мы запишем эти числа.
Прежде чем продолжать рассмотрение других систем, отметим два свойства обыкновенной десятичной записи числа, которые без изменений обобщаются на системы счисления по другому основанию. Первое из них непосредственно вытекает из определения позиционной записи. Если число представлено цифрами ![]() то его численное значение будет
то его численное значение будет ![]() например, для числа 3275 его значение вычисляется как
например, для числа 3275 его значение вычисляется как ![]() Второе свойство требует чуть более длинного объяснения, но, по большому счёту, ничуть не сложнее: если последовательно делить число на 10 с остатком и выписывать остатки, и так до тех пор, пока очередным частным не окажется ноль, то мы получим (в виде выписанных остатков) все цифры, составляющие это число, начиная с самой младшей. Например, поделим 3275 на 10 с остатком, получим 327 и 5 в остатке; поделим 327 на 10, получим 32 и 7 в остатке, поделим 32, получим 3 и 2 в остатке, поделим 3 на 10, получим 0 и 3 в остатке. Последовательность остатков выглядит так: 5, 7, 2, 3; это и есть цифры числа 3275.
Второе свойство требует чуть более длинного объяснения, но, по большому счёту, ничуть не сложнее: если последовательно делить число на 10 с остатком и выписывать остатки, и так до тех пор, пока очередным частным не окажется ноль, то мы получим (в виде выписанных остатков) все цифры, составляющие это число, начиная с самой младшей. Например, поделим 3275 на 10 с остатком, получим 327 и 5 в остатке; поделим 327 на 10, получим 32 и 7 в остатке, поделим 32, получим 3 и 2 в остатке, поделим 3 на 10, получим 0 и 3 в остатке. Последовательность остатков выглядит так: 5, 7, 2, 3; это и есть цифры числа 3275.
Оба этих свойства обобщаются на систему счисления по произвольному основанию, только вместо 10 в вычислениях нужно использовать соответствующее основание системы счисления. Например, для семеричной записи 15327 численное значение будет ![]() (естественно, все подсчёты мы выполняем в десятичной системе, поскольку нам так проще). Попробуем теперь выяснить, из каких цифр состоит семеричная запись числа 611, для чего последовательно выполним несколько делений на 7 с остатком. Результатом первого деления будет 87, в остатке 2; результатом второго — 12, в остатке 3; результатом третьего — 1, в остатке 5; результатом четвёртого — 0, в остатке 1. Итак, семеричная запись числа 611 состоит из цифр 2, 3, 5, 1, если перечислять их начиная с младшей, то есть эта запись — 15327 (где-то мы это уже видели).
(естественно, все подсчёты мы выполняем в десятичной системе, поскольку нам так проще). Попробуем теперь выяснить, из каких цифр состоит семеричная запись числа 611, для чего последовательно выполним несколько делений на 7 с остатком. Результатом первого деления будет 87, в остатке 2; результатом второго — 12, в остатке 3; результатом третьего — 1, в остатке 5; результатом четвёртого — 0, в остатке 1. Итак, семеричная запись числа 611 состоит из цифр 2, 3, 5, 1, если перечислять их начиная с младшей, то есть эта запись — 15327 (где-то мы это уже видели).
Как видим, первое из двух сформулированных свойств позиционной записи позволяет перевести число из любой системы счисления в ту, в которой мы привыкли проводить вычисления (для нас это система по основанию 10), а второе свойство — перевести число из привычной нам записи (то есть десятичной) в запись в произвольной системе счисления.
Отметим, что при переводе числа из “какой-то другой” системы в десятичную можно сэкономить на умножениях, представив
![]()
в виде
![]()
Например, всё то же 15327 можно перевести в десятичную систему, вычислив ((1∙7+5)∙7+3)∙7+2 = (12∙7+3)∙7+2 = 87∙7+2 = 609+2 = 611.
Можно заметить, что традиционный порядок записи чисел от старших цифр к младшим, к которому мы привыкли с детства, при переводах из одной системы счисления в другую часто оказывается не очень удобным; например, нам уже приходилось, выписав последовательность остатков от деления на основание, потом “переворачивать” эту последовательность, чтобы получить искомую запись числа. Более того, если немного подумать, мы заметим, что, видя в тексте какое-нибудь десятичное число, например, 2347450, мы, в сущности, не знаем, что обозначает первая же из его цифр; это, конечно, “два” (или “две”), но чего? Десятков тысяч? Сотен тысяч? Миллионов? Десятков миллионов? Выяснить это мы можем, лишь просмотрев запись числа до конца к узнав, сколько в нём цифр; только после этого, вернувшись к началу записи, мы поймём, что в этот раз двойка действительно означала два миллиона, а не что-то иное.
Но почему же весь мир использует именно такую “неудобную” запись? Ответ оказывается неожиданно прост: цифры, которые мы используем, не случайно называются арабскими; согласно господствующим историческим представлениям, современная система записи чисел была изобретена индийскими и арабскими математиками предположительно в VI-VII вв. н.э., а своего практически окончательного вида достигла в сохранившихся до наших дней работах знаменитого мудреца Аль-Хорезми (от чьего имени происходит слово “алгоритм”) и его современника Аль-Кинди; эти работы были написаны, согласно традиционной датировке, в IX веке. Так или иначе, арабская письменность предполагает начертание слов к строк справа налево, а не слева направо, как привыкли мы; так что для создателей десятичной системы счисления цифры в записи числа располагались именно так, как им было удобнее: при просмотре записи числа они сначала видели цифру, обозначающую единицы, потом цифру десятков, потом цифру сотен и так далее.
В программировании приходится часто сталкиваться с двоичной записью чисел, потому что именно так — в виде последовательностей нулей и единиц — в памяти компьютера представляются как числа, так и вся остальная информация. Поскольку выписывать ряды двоичных цифр оказывается не очень удобно, программисты в качестве сокращённой записи часто применяют системы счисления по основанию 16 и 8: каждая цифра восьмеричной записи числа соответствует трём цифрам двоичной записи того же числа, а каждая цифра шестнадцатеричной записи — четырём двоичным цифрам. Поскольку для шестнадцатеричной системы требуется шестнадцать цифр, а арабских цифр всего десять, к ним добавляют шесть первых букв латинского алфавита: А обозначает 10, В — 11, С —12, D — 13, Е — 14 и F — 15. Например, запись 3F16 означает 63, 10016 соответствует числу 256, а 11116 — числу 273.
При работе с современными компьютерами двоичные цифры (биты), как правило, объединяются в группы по восемь цифр (так называемые байты), что объясняет популярность шестнадцатеричной системы, ведь каждому байту соответствуют ровно две цифры такой записи: байт может принимать значения от 0 до 255, в шестнадцатеричной нотации это числа от 0016до FF16.
С восьмеричными цифрами такой фокус не проходит: для записи байта их требуется в общем случае три, потому что числа от 0 до 255 в восьмеричной системе представляются записями от 0008до 3778; но при этом тремя восьмеричными цифрами можно записать числа, в байт не помещающиеся, ведь максимальное трёхзначное восьмеричное число — 7778 — составляет 511. В частности, для записи трёх идущих подряд байтов нужно ровно восемь восьмеричных цифр, но на практике группы по три байта почти никогда не встречаются. Однако у восьмеричной системы счисления есть другое несомненное достоинство: она использует только арабские цифры. Собственно говоря, 8 есть максимальная степень двойки, не превосходящая 10; именно поэтому восьмеричная система была очень популярна у программистов до того, как восьмибитный байт стал устойчивой единицей измерения информации, но к настоящему времени она используется гораздо реже, чем шестнадцатеричная.
Поскольку цифр в двоичной системе всего две, перевод чисел в неё и из неё оказывается проще, чем с другими системами; в частности, если запомнить наизусть степени двойки (а у программистов это в любом случае получается само собой), при переводе в любую сторону можно обойтись без умножений. Пусть, например, нам нужно перевести в десятичную запись число 10011012; старшая единица, стоящая в седьмом разряде, соответствует шестой степени двойки, то есть 64, следующая единица стоит в четвёртом разряде и соответствует третьей степени двойки, то есть 8, следующая означает 4, и последняя, младшая — 1 (вообще говоря, младшая цифра равна самой себе в любой системе счисления). Складывая 64, 8, 4 и 1, получаем 77, это и есть искомое число.
Перевод из десятичной записи в двоичную можно выполнить двумя способами. Первый из них — традиционный: делить исходное число пополам с остатком, выписывая получающиеся остатки, пока в частном не останется ноль. Поскольку деление пополам нетрудно выполнить в уме, обычно всю операцию проводят, начертив на бумаге вертикальную линию; слева (и сверху вниз) записывают сначала исходное число, потом результаты деления, а справа выписывают остатки. Например, при переводе числа 103 в двоичную систему получается: 51 и 1 в остатке; 25 и 1 в остатке; 12 и 1 в остатке; 6 и 0 в остатке; 3 и 0 в остатке; 1 и 1 в остатке; 0 и 1 в остатке (см. рис. 1.11, слева). Остаётся только выписать остатки, просматривая их снизу вверх, и мы получим 11001112. Аналогично для числа 76 мы получим 38 и 0, 19 и 0, 9 и 1, 4 и 1, 2 и 0, 1 и 0, 0 и 1; выписывая остатки, получим 10011002 (там же, справа).

Рис. 1.11. Перевод в двоичную систему делением пополам
Есть и другой способ, основанный на знании степеней двойки. На каждом шаге мы выбираем наибольшую степень двойки, не превосходящую оставшееся число, после чего выписываем единицу в соответствующий разряд, а из числа соответствующую степень вычитаем. Пусть, например, нам потребовалось перевести в двоичную систему число 757. Наибольшая степень двойки, не превосходящая его — девятая (512), остаётся 245. Следующая степень двойки будет седьмая (128, поскольку 256 не подходит); останется 117. Дальше точно так же вычитаем 64, остаётся 53; вычитаем 32, остаётся 21; вычитаем 16, остаётся 5; вычитаем 4, остаётся 1, вычитаем 1 (нулевую степень двойки), остаётся 0. Результат будет 10111101012. Этот способ особенно удобен, если исходное число немного превосходит какую-то из степеней двойки: например, число 260 таким способом в “двоичку” переводится почти мгновенно: 256 + 4 = 1000001002.
Поскольку, как мы уже говорили, для сокращения записи двоичных чисел программисты часто употребляют системы счисления по основанию 16 и (чуть реже) 8, часто возникает потребность переводить из двоичной системы в эти две и обратно. К счастью, если основание одной системы счисления представляет собой натуральную степень п основания другой системы счисления, то одна цифра первой системы в точности соответствует п цифрам второй системы. На практике это свойство применяется только к переводам между двоичной системой и системами по основанию 8 и 16, хотя точно так же, например, можно было бы переводить числа из троичной системы в девятичную и обратно; просто ни троичная, ни девятичная системы счисления не нашли широкого практического применения.
Для перевода числа из восьмеричной системы в двоичную каждую цифру исходного числа заменяют соответствующими тремя двоичными цифрами (см. табл. 1.6). Например, для числа 37418это будут группы цифр 011 111 100 001, незначащий ноль можно будет отбросить, так что в результате получится 111111000012. Для перевода из шестнадцатеричной в двоичную делают то же самое, но каждую цифру заменяют на четыре двоичные цифры; например, для 2A3Fi6 получим 0010 1010 0011 1111, а после отбрасывания незначащих нулей — 101010001111112.
Таблица 1.6. Двоичное представление восьмеричных и шестнадцатеричных цифр
|
восьмеричные |
шестнадцатеричные |
||||
|
d8 |
bin |
d16 |
bin |
d16 |
bin |
|
0 |
000 |
0 |
0000 |
8 |
1000 |
|
1 |
001 |
1 |
0001 |
9 |
1001 |
|
2 |
010 |
2 |
0010 |
A |
1010 |
|
3 |
011 |
3 |
0011 |
В |
1011 |
|
4 |
100 |
4 |
0100 |
c |
1100 |
|
5 |
101 |
5 |
0101 |
D |
1101 |
|
6 |
110 |
6 |
0110 |
E |
1110 |
|
7 |
111 |
7 |
0111 |
F |
1111 |
Для перевода в обратную сторону исходное двоичное число справа налево (это важно) разбивают на группы по три или четыре цифры (соответственно для перевода в восьмеричную или шестнадцатеричную системы); если в старшей группе не хватает цифр, её дополняют незначащими нулями. Затем каждую получившуюся группу заменяют соответствующей цифрой. Рассмотрим, например, число 100001011110112. Для перевода в восьмеричную систему разобъём его на группы по три цифры, дописав справа незначащий ноль: 010000101111011; теперь каждую группу заменим на соответствующую восьмеричную цифру и получим 205738. Для перевода того же числа в шестнадцатеричную систему разобьём его на группы по четыре цифры, дописав в начало два незначащих нуля: 0010 0001 0111 1011; заменив их на соответствующие шестнадцатеричные цифры, получим 217A16.
Комбинации двоичных цифр, приведённые в таблице 1.6, программисты обычно просто помнят, но специально их зазубривать не обязательно: при необходимости их легко вычислить, а через некоторое время они сами собой уложатся в памяти.
Двоичные дроби переводятся в десятичную систему аналогично тому, как мы переводили целые числа, только цифрам после “двоичной запятой”36 соответствуют дроби ![]() и т.д. Например, для числа 101.011012 имеем
и т.д. Например, для числа 101.011012 имеем ![]() Можно поступить и иначе: сообразив, что один знак после “запятой” — это “половинки”, два знака — это “четвертинки”, три знака — “восьмушки” и так далее, мы можем рассмотреть всю дробную часть как целое число и разделить его на соответствующую степень двойки. В рассматриваемом случае у нас пять знаков после “запятой” — это тридцать вторые части, а 11012 есть 1310, так что имеем
Можно поступить и иначе: сообразив, что один знак после “запятой” — это “половинки”, два знака — это “четвертинки”, три знака — “восьмушки” и так далее, мы можем рассмотреть всю дробную часть как целое число и разделить его на соответствующую степень двойки. В рассматриваемом случае у нас пять знаков после “запятой” — это тридцать вторые части, а 11012 есть 1310, так что имеем ![]()
Обратный перевод дробного числа из десятичной системы в двоичную выполнить тоже несложно, но несколько труднее объяснить, почему это делается именно так. Для начала отдельно переводим целую часть числа, выписываем результат и забываем о ней, оставив только десятичную дробь, заведомо меньшую единицы. Далее нам необходимо выяснить, сколько половинок (одна или ни одной) у нас имеется в этой дробной части. Для этого достаточно умножить её на два. В полученном числе целая часть может быть равна нулю или единице, это и есть искомое “количество половинок” в исходном числе. Какова бы ни была полученная целая часть, мы выписываем её в качестве очередной двоичной цифры, а из рабочего числа убираем, поскольку уже учли её в результате. Оставшееся число снова представляет собой дробь, заведомо меньшую единицы, ведь целую часть мы только что отсекли; умножаем эту дробь на два, чтобы определить “количество четвертинок”, выписываем, отсекаем, умножаем на два, определяем “количество восьмушек” и так далее.
Например, для уже знакомого нам числа 5.40625 перевод обратно в двоичную систему будет выглядеть так. Целую часть сразу же переводим как обычное целое число, получаем 101, выписываем результат, ставим двоичную точку и на этом забываем про целую часть нашего исходного числа. Остаётся дробь 0.40625. Умножаем её на два, получаем 0.8125. Поскольку целая часть равна нулю, выписываем в результат цифру 0 (сразу после запятой) и продолжаем процесс. Умножение 0.8125 на два даёт 1.625; выписываем в результат единичку, убираем её из рабочего числа (получается 0.625), умножаем на два, получаем 1.25, выписываем единичку, умножаем 0.25 на два, получаем 0.5, выписываем ноль, умножаем на два, получаем 1.0, выписываем единичку. На этом перевод заканчивается, поскольку в рабочем числе у нас остался ноль, и его, понятное дело, сколько ни умножай, будут получаться одни нули; заметим, в принципе мы имеем право так делать — ведь к полученной двоичной дроби можно при желании дописать справа сколько угодно нулей, все они будут незначащие. Выписанный результат у нас получился 101.011012, что, как мы видели, как раз и есть двоичное представление числа 5.40625.
Далеко не всегда всё будет столь благополучно; в большинстве случаев вы получите бесконечную (но, конечно, периодическую) двоичную дробь. Чтобы понять, почему это происходит так часто, достаточно вспомнить, что любую конечную или периодическую десятичную дробь можно представить в виде несократимой простой дроби с целым числителем и натуральным знаменателем; собственно говоря, это есть определение рационального числа. Так вот, нетрудно видеть, что в виде конечной двоичной дроби представимы такие и только такие рациональные числа, у которых в знаменателе степень двойки. Конечно, аналогичное ограничение присутствует и для десятичных дробей, а также и в системе счисления по вообще любому основанию, но в общем случае это ограничение формулируется мягче: рациональное число, представленное в виде несократимой дроби m/n, представимо в виде конечной дроби в системе по основанию Nтогда и только тогда, когда существует целая степень числа N, делящаяся нацело на n. В частности, дробь 49/50 можно представить в виде конечной десятичной дроби, потому что 102 = 100 делится на 50 нацело; аналогично можно записать в виде конечной десятичной дроби число 77/80, потому что на 80 без остатка поделится 104 = 10000. В общем случае у нас несократимая простая дробь превратится в конечную десятичную, если её знаменатель раскладывается на простые множители в виде 2k ∙ 5m: при этом нам достаточно выбрать большее из k и m и использовать его в качестве степени, в которую возвести 10.
Для случая двоичной системы всё жёстче: степень двойки, какова бы она ни была, нацело может поделиться только на другую степень двойки. В применении к переводу из десятичной системы в двоичную следует заметить, что любая десятичная дробь есть число вида n/10k; чтобы в знаменателе остались одни двойки, необходимо, чтобы числитель нужное число раз делился на пять. Так, рассмотренное в примере выше 5.40625 есть 540625/105, но числитель 540625 прекрасно делится без остатка на 55 = 3125 (результатом деления будет 173), поэтому после сокращения нужного числа пятёрок в знаменателе остаётся степень двойки, что и позволяет записать это число в виде конечной двоичной дроби. Но так, конечно, происходит не всегда; в большинстве случаев (в частности, всегда, когда последняя значащая десятичная цифра дроби отлична от 5) получаемая двоичная дробь окажется бесконечной, хотя и периодичной. В таком случае нужно выполнять описанную выше процедуру с последовательным умножением на два, пока вы не получите рабочее число, которое уже видели; это будет означать, что вы попали в период; напомним, что периодическая дробь записывается путём заключения её периода в круглые скобки. Например, для числа 0.3510 у нас получится 0.7 (выписываем 0), 1.4 (выписываем 1, оставляем 0.4), 0.8 (выписываем 0), 1.6 (выписываем 1, оставляем 0.6), 1.2 (выписываем 1, оставляем 0.2) — и, наконец, 0.4, которое мы уже видели четыре шага назад. Следовательно, период дроби составляет четыре цифры, а в результате 0.3510 = 0.01(0110)2.
1.5.3. Двоичная логика
В программировании мы часто сталкиваемся с проверками всевозможных условий, таких как “не слишком ли длинная строка”, “не оказался ли дискриминант отрицательным”, “хватит ли нам отведённого пространства”, “существует ли нужный файл”, “выбрал ли пользователь этот вариант работы или другой” и прочее; начав программировать, мы очень быстро убедимся, что выполнение даже самых простых программ основано на проверках условий. При этом сами условия представляют собой логические выражения, то есть такие выражения, которые вычисляются, а результатом вычисления становится логическое значение — ложь или истина.
Раздел математики, в котором изучаются выражения такого рода, называется математической логикой; надо сказать, что это достаточно сложная область знаний, включающая множество нетривиальных теорий, и на глубокое изучение математической логики может уйти вся жизнь. Мы в нашей книге рассмотрим только одну из самых примитивных составляющих математической логики — так называемую алгебру двоичной логики.
По своей сути двоичная логика похожа на арифметику, но вместо бесконечного множества чисел здесь используется множество, состоящее всего из двух значений: 0 (ложь) и 1 (истина). Над этими значениями определены разные операции, результатом которых тоже является 0 или 1. Одной из самых простых логических операций является отрицание, “не x”, которое обозначается ![]() в книгах можно встретить также другие обозначения, например ¬х. Операция отрицания меняет значение на противоположное, то есть
в книгах можно встретить также другие обозначения, например ¬х. Операция отрицания меняет значение на противоположное, то есть ![]() = 0 и
= 0 и ![]() = 1. Поскольку у операции отрицания всего один аргумент, говорят, что она унарная.
= 1. Поскольку у операции отрицания всего один аргумент, говорят, что она унарная.
Самыми известными и часто употребляемыми логическими бинарными операциями, то есть операциями двух аргументов, можно считать логическое или и логическое и, которые в математике называются также дизъюнкцией и конъюнкцией. “Логическое или” между двумя логическими значениями будет истинно, когда хотя бы одно из исходных значений истинно; естественно, они могут быть истинными одновременно, тогда “логическое или” между ними тоже останется истинным. Единственный вариант, когда “логическое или” оказывается ложным — это когда оба его аргумента ложны. “Логическое и”, напротив, истинно тогда и только тогда, когда истинны оба его аргумента, а во всех остальных случаях ложно.
Операция “логического или” обычно обозначается знаком “V”, что касается операции “логического и”, то наиболее популярное обозначение для неё — амперсанд “&”, но во многих современных учебниках эту операцию почему-то предпочитают обозначать знаком “Л”.
Помимо конъюнкции и дизъюнкции, достаточно часто встречаются операции исключающее или и импликация. “Исключающее или”, обозначаемое знаком “⊕”, истинно, когда истинен один из его аргументов, но не оба сразу; от обычного “или” эта операция отличается своим значением для случая обоих истинных аргументов.
Операция импликации (обозначается “→”) несколько более сложна для понимания. Она основана на принципе, что в рассуждениях из истинных посылок может следовать только истина, а вот из ложных посылок может следовать что угодно, то есть может получиться истина, а может — ложь. Чтобы понять, почему это так, можно припомнить, что далеко не все научные теории были истинными, но при этом замечательно использовались и даже давали правильные результаты. В частности, известно, что братья Монгольфье подняли в воздух первый в истории воздушный шар, наполнив его дымом от смеси соломы и шерсти; солому они рассматривали как растительное начало жизни, а шерсть — как животное начало, что, по их мнению, должно было привести к возможности полёта, и полёт действительно состоялся, несмотря на то, что животное и растительное начало к этому не имели никакого отношения. Иначе говоря, возможно получить абсолютно правильный результат, отталкиваясь от абсолютно ложных посылок. В соответствии с этим импликация ложна лишь в том случае, если её левый аргумент — истина, а правый — ложь (из истины ложь следовать не может), во всех остальных случаях импликация считается истинной.
Если обозначить множество {0,1} буквой В37, то логические операции двух аргументов можно рассматривать как функции, областью определения которых является В х В (то есть множество пар {(0, 0), (0,1), (1,0), (1,1)}), а областью значений — само В. Поскольку область определения логических функций конечна, их можно задавать таблицами, в которых в явном виде указано значение для каждого элемента из области определения. Такие таблицы для логических функций называются таблицами истинности; в частности, таблица 1.7 содержит таблицу истинности для рассмотренных нами конъюнкции, дизъюнкции, “исключающего или” и импликации.
Таблица 1.7. Основные бинарные логические операции
|
аргументы х у |
конъюнкция х&у, х Λ у |
дизъюнкция х V у |
искл. или х ⊕ у |
импликация x → у |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
Поскольку логическая функция двух аргументов полностью определяется своими значениями, которых у неё четыре, то есть, попросту говоря, набором из четырёх двоичных значений, мы, припомнив наши знания комбинаторики, можем заключить, что всего их существует 16. Множество всех возможных логических функций двух аргументов показано в таблице 1.8, где они упорядочены по возрастанию их набора значений, как если бы набор значений был записью двоичного числа. Начинается перечисление с функции “константа 0”, которая ложна для любых аргументов, а заканчивается “константой 1”, или тавтологией — функцией, которая, напротив, на любых аргументах истинна. Как можно легко убедиться, таблица содержит, в числе прочего, только что рассмотренные нами конъюнкцию, дизъюнкцию, импликацию и “исключающее или”. Кроме того, в таблице обнаруживаются функции ж (всегда равна первому аргументу, независимо от второго) и у (всегда равна второму аргументу, независимо от первого), а также их отрицания; функции, обозначенные как “↓” и “|”, называются соответственно “стрелка Пирса” и “штрих Шеффера” и представляют собой отрицание дизъюнкции и отрицание конъюнкции:
![]()
Таблица 1.8. Все возможные двоичные функции двух аргументов
|
x |
y |
0 |
& |
> |
x |
< |
y |
⊕ |
V |
↓ |
≡ |
|
← |
|
→ |
| |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Функция, обозначенная знаком “≡”, называется эквивалентностью: она истинна, когда её аргументы равны, и ложна, если аргументы различаются. Нетрудно убедиться, что эквивалентность представляет собой отрицание “исключающего или”. Остаются ещё три функции, это “импликация наоборот” (“x ← у = у → x”), а также функции “больше” и “меньше”, которые представляют собой отрицание импликаций. Итого, начав с констант, мы перечислили ровно 16 функций, то есть все.
Если рассмотреть логические функции трёх аргументов, то область их определения — множество В х В х В — состоит из восьми троек {(0, 0, 0), (0, 0,1), (0,1, 0), ..., (1,1,0), (1,1,1)}; как следствие, логическая функция трёх аргументов определяется набором из восьми значений, а всего таких функций будет 28 = 256. В общем случае логическая функция п аргументов определена на множестве мощности 2n и определяется, соответственно, упорядоченным набором из 2n значений, а всего таких функций, очевидно, ![]() . Так, функций от четырёх аргументов оказывается 216 = 65536, функций от пяти аргументов — 232 = 4294967296 и так далее. Если в этом абзаце что-то показалось непонятно, перечитайте параграф о комбинаторике; если и это не помогло, обязательно найдите кого-нибудь, кто сможет вам объяснить, что тут происходит. Дело здесь, разумеется, не в количестве функций; но если вы тут чего-то не поняли, то у вас определённо есть проблемы с простейшей комбинаторикой, а вот это уже никуда не годится.
. Так, функций от четырёх аргументов оказывается 216 = 65536, функций от пяти аргументов — 232 = 4294967296 и так далее. Если в этом абзаце что-то показалось непонятно, перечитайте параграф о комбинаторике; если и это не помогло, обязательно найдите кого-нибудь, кто сможет вам объяснить, что тут происходит. Дело здесь, разумеется, не в количестве функций; но если вы тут чего-то не поняли, то у вас определённо есть проблемы с простейшей комбинаторикой, а вот это уже никуда не годится.
Вернувшись к функциям двух аргументов, отметим, что конъюнкция и дизъюнкция во многом аналогичны умножению и сложению: так, конъюнкция с нулём, как и умножение на ноль, всегда даёт ноль; конъюнкция с единицей, как и умножение на единицу, всегда даёт исходный аргумент; дизьюнкция с нулём, как и сложение с нулём, тоже всегда даёт исходный аргумент. Из-за этого сходства математики часто в формулах опускают обозначение конъюнкции, будь то “x & у” или “x Λ у”, и пишут просто “ху” или “х ∙ у”. В частности:
х ∙ 0 = 0 х ∙ 1= х х V 0 = х х V 1 = 1
Запоминать эти соотношения не надо! Достаточно вспомнить, что означает конъюнкция или дизъюнкция, и все четыре приведённых соотношения оказываются совершенно очевидны. В самом деле, конъюнкция равна единице только при обоих единичных аргументах, так что если один из аргументов конъюнкции равен нулю, то каков бы ни был второй, вся она вместе уже единицей не станет, т. е. х ∙ 0 = 0; в то же время если один из её аргументов уже заведомо единица, то нужно, чтобы второй был единицей, тогда и вся она окажется единицей, иначе она будет нулём; тоесть при одном из аргументов заведомо единичном конъюнкция равна второму аргументу: х ∙ 1 = х. Аналогично если один из аргументов дизъюнкции заведомо единичный, то этого достаточно, и в ноль её уже не превратить, т. е. х V 1 = 1; ну а если один из аргументов дизъюнкции — ноль, то это ещё не приговор, ведь второй может оказаться единицей, и тогда она вся будет единицей: х V 0 = х.
Точно так же не нуждаются в запоминании соотношения, позволяющие раскрывать скобки в выражениях, состоящих из конъюнкции, дизъюнкции и отрицания:
(х V y)z = xz V yz (xу) V z = (х V z)(y V z)
Первое соотношение получается из рассуждения “для истинности всего выражения слева необходимо и достаточно, чтобы хотя бы одна из двух переменных х и у была истинна, при этом чтобы была истинна переменная z; но это то же самое, как если сказать, что нам нужно, чтобы или оказались одновременно истинными х и z (истинная х сделает истинной скобку, z должна быть истинной, иначе конъюнкция не может быть истинной), или по тем же причинам должны быть одновременно истинными у и z”. Второе соотношение получается рассуждением “истинность выражения могут обеспечить или истинность z, или одновременная истинность х и у; это то же самое, как сказать, что у нас должны быть одновременно истинными две скобки, причём истинность первой из них может обеспечить либо х, либо z, а истинность второй — либо у, либо z”.
Приведём ещё несколько элементарных соотношений:
![]()
Их, разумеется, тоже не нужно запоминать. Соответствующие рассуждения предлагаем читателю найти самостоятельно.
Отдельного упоминания заслуживают так называемые законы де Моргана:
![]()
Почему-то то обстоятельство, что эти соотношения являются именными, то есть носят имя человека, якобы их открывшего, нагоняет на многих новичков изрядный страх; уж если эти соотношения кому-то потребовалось “открывать”, да ещё за это открытие соотношения назвали именем того, кто их открыл, то тут уж точно без зубрёжки никак. Между тем здесь на самом деле всё совершенно элементарно. Первое соотношение: “Что нам нужно, чтобы сделать ложной дизъюнкцию? Если хотя бы один аргумент будет истинным, то она вся станет истинной; следовательно, для её ложности необходимо, чтобы оба аргумента были ложными, то есть и х был ложным, и у был ложным”. Второе соотношение: “Что нам нужно, чтобы сделать ложной конъюнкцию? Очевидно, достаточно, чтобы хотя бы один из её аргументов был ложным”. Вот вам и все “великие и ужасные” законы де Моргана.
В заключение обзора двоичной логики дадим одну рекомендацию. Если вам пришлось решать задачу, в которой дана некая логическая формула и с ней что-то предлагается сделать, то для начала убедитесь, что в формуле применяются только конъюнкция, дизъюнкция и отрицание. Если это не так, немедленно избавьтесь от всех остальных знаков операций, сведя их к первым трём; отметим, что это всегда можно сделать. Возьмём, например, загадочную импликацию. Для её истинности достаточно, чтобы первый аргумент был ложным (ведь из лжи может следовать что угодно); точно так же достаточно, чтобы второй аргумент был истинным (ведь истина может следовать как из истины, так и из лжи). Получаем, что
![]()
Точно так же, если вам встретилось “исключающее или”, замените его одним из следующих способов: “один из аргументов должен быть истинным, но не два одновременно” или “нужно, чтобы один был ложным, другой истинным, или наоборот”:
![]()
Заметим, что из первого раскрытием скобок получается второе:
![]()
Между прочим, в аналогичном виде можно записать вообще любую логическую функцию от произвольного количества переменных, просто посмотрев на её таблицу истинности. Выбрав те строки, где значение функции — 1, мы для всех таких строк выписываем конъюнкты, состоящие из всех переменных, причём те, которые в этой строке равны нулю, в конъюнкт входят со знаком отрицания. Все полученные конъюнкты (которых будет столько, на скольких наборах переменных функция равна единице) записываем через знак дизъюнкции. Например, для стрелки Пирса соответствующая запись будет состоять из одного конъюнкта ![]() а для штриха Шеффера — из трёх конъюнктов
а для штриха Шеффера — из трёх конъюнктов ![]() Если же, к примеру, мы рассмотрим функцию трёх аргументов f(x,y,z), которая равна единице на четырёх наборах {(0, 0, 0), (0, 0,1), (0,1,1), (1,1,1)}, а на всех остальных наборах равна нулю, то соответствующее выражение для этой функции будет выглядеть так:
Если же, к примеру, мы рассмотрим функцию трёх аргументов f(x,y,z), которая равна единице на четырёх наборах {(0, 0, 0), (0, 0,1), (0,1,1), (1,1,1)}, а на всех остальных наборах равна нулю, то соответствующее выражение для этой функции будет выглядеть так: ![]() Такая форма записи логической функции называется дизъюнктивной нормальной формой (ДНФ).
Такая форма записи логической функции называется дизъюнктивной нормальной формой (ДНФ).
1.5.4. Виды бесконечности
Материал этого параграфа может показаться вам слишком “заумным”; в принципе, следует признать, что к практическому программированию всё это прямого отношения не имеет, или, точнее говоря, программировать можно без этого. К сожалению, если вы пропустите этот параграф, то следующие параграфы этой главы, в которых рассказывается про алгоритмы и теорию вычислимости, вы тоже не поймёте; но если математика вам уже надоела, вы можете спокойно пропустить их все. Никто не мешает вернуться сюда позже, когда вы будете к этому готовы. Если вы действительно решите пропустить остаток “математической” главы, запомните только одну вещь: термин “алгоритм” на самом деле гораздо сложнее, чем о нём принято думать. В частности, определения алгоритма не существует и существовать не может, причём вообще ни в каком виде и ни в каком смысле. О том, почему это так, рассказывается в следующем параграфе.
Вернёмся к нашему предмету обсуждения. Из школьного курса математики мы знаем, что, например, чисел существует “бесконечно много”; этот факт выражается в том, что, сколь бы огромное число мы ни взяли, мы всегда можем прибавить к нему единицу, получив число ещё большее. В школе обычно этим и удовлетворяются, но в курсе высшей математики приходится отметить, что бесконечности бывают разные. “Наименьшая” из них — это так называемая счётная бесконечность; множество считается счётно-бесконечным, если его элементы можно перенумеровать натуральными числами в каком-то порядке. Простейший пример счётной бесконечности — само по себе множество натуральных чисел: числу 1 мы дадим номер первый, числу 2 — номер второй и так далее. Множество целых чисел (в которое, наряду с натуральными, входят также ноль и отрицательные целые, то есть “натуральные с минусом”) также является счётно-бесконечным: например, можно первый номер отдать числу 0, второй номер — числу 1, третий номер — числу -1, числа 2 и —2 получат соответственно четвёртый и пятый номера, и так далее; каждое положительное число к при этом получает номер 2k, а каждое отрицательное число — m — номер 2m + 1 (например, число 107 получит номер 214, а число —751 — номер 1503). Множество чётных натуральных чисел тоже счётное: число 2 получает номер первый, число 4 — номер второй, и так до бесконечности, то есть каждое число вида 2n получает номер n. Получается, что натуральных чисел ровно столько же, сколько натуральных чётных, и, с другой стороны, ровно столько же, сколько всех целых. “Количество” натуральных чисел математики обозначают символом ![]() (читается “алеф-нуль”).
(читается “алеф-нуль”).
При внимательном рассмотрении оказывается, что множество рациональных чисел, то есть чисел, представимых в виде несократимой дроби m/n, где m — целое, а n — натуральное, — тоже счётное. Чтобы их занумеровать, представьте себе координатную полуплоскость, где по горизонтальной оси откладываются значения знаменателя дроби — напомним, таковые должны быть натуральными, то есть начинаться с единицы, — а по вертикальной откладываются значения числителя. Иначе говоря, нам нужно придумать некую нумерацию для целочисленных точек координатной плоскости, лежащих справа от вертикальной оси, при этом нужно, чтобы в нумерацию каждое число попало только один раз, то есть, например, дробям ![]() и т. д. приписывать различные номера не нужно, ведь эти дроби обозначают одно и то же число. Впрочем, это как раз просто: при нумерации следует, во-первых, пропускать все сократимые дроби, а во-вторых, все дроби с числителем 0, кроме самой первой такой дроби 0/1, которая будет обозначением нуля. Простейший пример такой нумерации строится “уголками”, расходящимися от начала координат. Номер первый мы дадим дроби 0/1. На первый “уголок” попадут дроби 1/1, 0/2 и -1/1, но дробь 0/2 мы, как договорились, пропустим, а вот две остальные (числа 1 и -1) получат номера второй и третий. Двигаясь вдоль следующего “уголка”, занумеруем: 2/1 (№4), 1/2 (№5), 0/3 (пропускаем), -1/2 (№6) и -2/1 (№7). На следующем после этого “уголке” мы уже будем вынуждены пропускать сократимые дроби: 3/1 (№8), 2/2 (пропускаем), 1/3 (№9), 0/4 (пропускаем), -1/3 (№10), -2/2 (пропускаем), -3/1 (№11). Продолжая процесс “до бесконечности”, мы припишем натуральные номера всем рациональным числам.
и т. д. приписывать различные номера не нужно, ведь эти дроби обозначают одно и то же число. Впрочем, это как раз просто: при нумерации следует, во-первых, пропускать все сократимые дроби, а во-вторых, все дроби с числителем 0, кроме самой первой такой дроби 0/1, которая будет обозначением нуля. Простейший пример такой нумерации строится “уголками”, расходящимися от начала координат. Номер первый мы дадим дроби 0/1. На первый “уголок” попадут дроби 1/1, 0/2 и -1/1, но дробь 0/2 мы, как договорились, пропустим, а вот две остальные (числа 1 и -1) получат номера второй и третий. Двигаясь вдоль следующего “уголка”, занумеруем: 2/1 (№4), 1/2 (№5), 0/3 (пропускаем), -1/2 (№6) и -2/1 (№7). На следующем после этого “уголке” мы уже будем вынуждены пропускать сократимые дроби: 3/1 (№8), 2/2 (пропускаем), 1/3 (№9), 0/4 (пропускаем), -1/3 (№10), -2/2 (пропускаем), -3/1 (№11). Продолжая процесс “до бесконечности”, мы припишем натуральные номера всем рациональным числам.
Предложение “продолжать процесс до бесконечности” может показаться неконструктивным, ведь в нашем распоряжении нет и не может быть “бесконечного” времени, но в данном случае бесконечное время нам и не нужно. Важно то, что каково бы ни было рациональное число, мы сможем установить, какой именно номер оно имеет в нашей нумерации, причём сделать это мы сможем за конечное время, сколь бы “заковыристое” число нам ни дали.
Можно очень легко доказать, что множество бесконечных десятичных дробей (то есть тех самых иррациональных38 чисел) счётным не является. В самом деле, пусть мы придумали некую нумерацию бесконечных десятичных дробей. Рассмотрим теперь, например, дробь, имеющую нулевую целую часть; в качестве её первой цифры после запятой возьмём любую цифру, кроме той, которая является первой цифрой в дроби №1; в качестве второй — любую, кроме той, которая является второй цифрой в дроби №2, и так далее. Полученная дробь будет заведомо отличаться от каждой дроби из попавших в нашу нумерацию, ведь от дроби с номером n она отличается по меньшей мере цифрой в n-ной позиции после запятой. Получается, что в нашей (бесконечной!) нумерации эта новая дробь номера не имеет, причём это никак не зависит от того, как конкретно мы попытались занумеровать дроби. Нетрудно видеть, что таких “неучтённых” дробей — бесконечное количество, хотя, на самом деле, это не так уж важно. Итак, никакая нумерация не может охватить всё множество бесконечных десятичных дробей. Применённая здесь схема доказательства носит название канторовского диагонального метода в честь придумавшего её немецкого математика Георга Кантора.
Говорят, что множество бесконечных десятичных дробей имеет мощность континуум; математики обозначают это символом ![]() (“алеф-один”). Чтобы понять, насколько это “много”, проведём некий мысленный эксперимент, тем более что его результаты нам пригодятся при рассмотрении теории алгоритмов. Пусть у нас есть некий алфавит, то есть некое конечное множество “символов”, чем бы эти символы ни были: это могут быть буквы, цифры, вообще любые знаки, но с таким же успехом это могут быть вообще элементы любой природы, лишь бы их было конечное множество. Обозначим алфавит буквой А. Рассмотрим теперь множество всех конечных цепочек, составленных из символов алфавита А, то есть множество конечных последовательностей вида a1, а2, а3, ... аk, где каждое ai ∈ А. Такое множество, включающее в себя пустую цепочку (цепочку длины 0), обозначают А*. Нетрудно видеть, что, коль скоро алфавит конечен и каждая отдельно взятая цепочка тоже конечна (хотя их длину мы не ограничиваем, то есть можно рассматривать цепочки длиной в миллиард символов, в триллион, в триллион триллионов и так далее), всё множество цепочек окажется счётным. В самом деле, пусть алфавит включает п символов. Пустая цепочка получит номер 1; цепочки из одного символа получат номера с 2 по n + 1; цепочки из двух символов, которых в общей сложности n2, получат номера с n + 2 по n2 + n + 1; аналогично номера цепочек из трёх символов начнутся с n2 + n + 2 и закончатся номером n3 + n2 + n + 1 и так далее.
(“алеф-один”). Чтобы понять, насколько это “много”, проведём некий мысленный эксперимент, тем более что его результаты нам пригодятся при рассмотрении теории алгоритмов. Пусть у нас есть некий алфавит, то есть некое конечное множество “символов”, чем бы эти символы ни были: это могут быть буквы, цифры, вообще любые знаки, но с таким же успехом это могут быть вообще элементы любой природы, лишь бы их было конечное множество. Обозначим алфавит буквой А. Рассмотрим теперь множество всех конечных цепочек, составленных из символов алфавита А, то есть множество конечных последовательностей вида a1, а2, а3, ... аk, где каждое ai ∈ А. Такое множество, включающее в себя пустую цепочку (цепочку длины 0), обозначают А*. Нетрудно видеть, что, коль скоро алфавит конечен и каждая отдельно взятая цепочка тоже конечна (хотя их длину мы не ограничиваем, то есть можно рассматривать цепочки длиной в миллиард символов, в триллион, в триллион триллионов и так далее), всё множество цепочек окажется счётным. В самом деле, пусть алфавит включает п символов. Пустая цепочка получит номер 1; цепочки из одного символа получат номера с 2 по n + 1; цепочки из двух символов, которых в общей сложности n2, получат номера с n + 2 по n2 + n + 1; аналогично номера цепочек из трёх символов начнутся с n2 + n + 2 и закончатся номером n3 + n2 + n + 1 и так далее.
Рассмотрим теперь алфавит, состоящий из всех символов, когда-либо использовавшихся в книгах на Земле. Включим туда латиницу, кириллицу, греческий алфавит, арабские письмена, экзотические азбуки, используемые в грузинском и армянском языке, все китайские, японские и корейские иероглифы, вавилонскую клинопись, иероглифику древнего Египта, скандинавские руны, добавим цифры и все математические значки, подумаем некоторое время, не забыли ли чего-нибудь, добавим всё, что припомним или что нам посоветуют знакомые. Ясно, что такой супер-алфавит, несмотря на его довольно внушительные размеры, будет всё же конечен. Обозначим его буквой V и посмотрим, что у нас в результате попадёт в множество цепочек V* (напомним, цепочки мы тоже рассматриваем только конечные).
Очевидно, в это множество угодят все книги, когда-либо написанные на Земле. Мало того, туда же попадут все книги, которые ещё не написаны, но когда-нибудь будут39; все книги, которые никогда не были и не будут написаны, но теоретически могли бы быть написаны; а равно и такие, которые никто и никогда не стал бы писать — например, все книги, текст которых представляет собой хаотическую последовательность символов из разных систем письменности, где немецкая буква ![]() соседствует с дореволюционной русской
соседствует с дореволюционной русской ![]() а японские иероглифы перемежаются вавилонской клинописью.
а японские иероглифы перемежаются вавилонской клинописью.
Если вам и этого мало, представьте себе книгу толщиной в радиус Солнечной системы, а диагональю листа как от нас до соседней галактики, при этом набранную обычным 12-м шрифтом; ясно, что физически такую книгу сделать невозможно, но, тем не менее, в множество V* войдёт не просто “эта книга”, в него войдут все такие книги, отличающиеся друг от друга хотя бы одним символом. И не только эти, Вселенная ведь бесконечна! Кто мешает представить себе книгу размером в миллиард световых лет? А все такие книги?
Если ваше воображение ещё не дало сбоя, вам можно только позавидовать. И после всего этого мы вспоминаем, что множество V* “всего лишь” счётное! Чтобы получить континуум, нам надо рассматривать не просто книги несуразно огромных размеров, нам потребуются бесконечные книги, такие, у которых вообще нет размера, которые никогда не кончаются, сколько бы мы ни двигались вдоль текста; в сравнении с этим книга форматом в миллиард световых лет оказывается чем-то вроде детской игрушки. Причём сама такая “бесконечная книга”, отдельно взятая, ещё не даёт континуума, она ведь всего одна; нет, нам нужно рассмотреть все бесконечные книги, и вот тогда мы увидим, что рассматриваемое множество (бесконечных книг) имеет мощность континуум. Вот только не вполне понятно, как именно мы собираемся эти бесконечные книги “рассматривать”, особенно прямо во всём их многообразии, если мы даже одну такую книгу представить себе толком не можем.
Вполне очевидно, что оперировать континуальными бесконечностями в каком бы то ни было конструктивном смысле невозможно; счётные бесконечности представляют собой абсолютный предел не только для человеческого, но и для любого другого мозга, если только такой мозг не окажется бесконечным сам по себе. Откровенно говоря, даже работая со счётными бесконечностями, мы никогда не рассматриваем сами бесконечности, мы просто заявляем, что каков бы ни был элемент N, всегда найдётся элемент N + 1; иначе говоря, каков бы ни был уже рассмотренный набор элементов множества, мы всегда придумаем ещё один элемент, который входит во множество, но ещё не рассмотрен в предложенном наборе. Здесь, по большому счёту, нет никакой “бесконечности”, есть просто наш отказ от рассмотрения некоего “потолка”, выше которого почему-то запрещено прыгать.
При всём при этом в математике рассматриваются не только континуальные бесконечности, но и бесконечности, превосходящие континуум: простейшим примером такой бесконечности может послужить множество всех множеств действительных чисел (его мощность обозначают ![]() ). Конечно, никакого конструктивного смысла такие построения не несут; коль скоро мы ставим себе прикладные задачи, появление в наших рассуждениях континуальной бесконечности должно служить своего рода “тревожной лампочкой”: осторожно, выход за пределы конструктивного. Значит ли это, что математика чем-то плоха? Разумеется, нет; просто математика вовсе не обязана быть конструктивной. Математики постоянно проверяют на прочность границы возможностей человеческого мышления, и за одно это им следует сказать огромное спасибо, как, кстати, и за то, что именно математики обеспечивают широкую публику средствами для развития возможностей мозга; ради одного только этого эффекта — развития собственных интеллектуальных возможностей — математику, несомненно, стоит изучать. Просто не всякая математическая модель пригодна для прикладных или, если угодно, инженерных целей; само по себе это не плохо и не хорошо, это просто факт.
). Конечно, никакого конструктивного смысла такие построения не несут; коль скоро мы ставим себе прикладные задачи, появление в наших рассуждениях континуальной бесконечности должно служить своего рода “тревожной лампочкой”: осторожно, выход за пределы конструктивного. Значит ли это, что математика чем-то плоха? Разумеется, нет; просто математика вовсе не обязана быть конструктивной. Математики постоянно проверяют на прочность границы возможностей человеческого мышления, и за одно это им следует сказать огромное спасибо, как, кстати, и за то, что именно математики обеспечивают широкую публику средствами для развития возможностей мозга; ради одного только этого эффекта — развития собственных интеллектуальных возможностей — математику, несомненно, стоит изучать. Просто не всякая математическая модель пригодна для прикладных или, если угодно, инженерных целей; само по себе это не плохо и не хорошо, это просто факт.
Примечательна ситуация с вопросом о том, существуют ли такие множества, которые нельзя занумеровать (то есть несчётные), но которые при этом “меньше”, чем континуум; иными словами, есть ли ещё какие-нибудь бесконечности между счётной и континуальной. Существование таких бесконечностей невозможно ни доказать, ни опровергнуть, то есть мы вправе считать, что таких множеств не бывает, но точно так же мы вправе считать, что они бывают. В любом случае, ещё никому не удалось и вряд ли когда-нибудь удастся конструктивно построить такое множество, то есть описать элементы, из которых оно будет состоять, подобно тому, как мы описывали натуральные числа для счётных множеств и бесконечные десятичные дроби для континуумов.
1.5.5. Алгоритмы и вычислимость
Рассказывая об истории компьютеров, мы отметили, что работа компьютера состоит в проведении вычислений, хотя результаты этих вычислений в большинстве случаев не имеют ничего общего с числами: любая информация, с которой работает компьютер, должна быть представлена в некоторой объективной форме, и, как следствие, правила, по которым из одной информации получается другая (а именно это и делает компьютер), суть не что иное, как функции в сугубо математическом смысле слова: в роли области определения такой функции выступает множество неких “порций информации”, представленных избранным объективным способом, и оно же служит областью значений. Обычно считается, что информация — как исходная, так и получаемая — представляется в виде цепочек символов в некотором алфавите40 А, то есть каждая “порция информации” есть элемент уже знакомого нам по предыдущему параграфу множества А*. С учётом этого мы можем считать, что работа компьютера всегда состоит в вычислении некой функции вида А* → А* (выражение X → Y обозначает функцию с областью определения X и областью значений Y). При этом мы можем легко заметить определённую проблему. Коль скоро мы можем вычислить значение функции (в каком бы то ни было смысле), то, очевидно, мы можем как-то записать наши промежуточные вычисления, то есть представить вычисление в виде текста. Больше того, если функция в каком-то смысле может быть вычислена, то, видимо, в виде текста можно представить вообще само по себе правило, как эту функцию надо вычислять. Множество всех возможных текстов, как мы уже знаем, счётное. Между тем с помощью всё того же канторовского диагонального метода легко убедиться, что множество всех функций над натуральными числами имеет мощность континуум; если заменить тексты, то есть элементы множества А*, их номерами (а это можно сделать в силу счётности множества А*), получится, что функций вида А* → А* тоже континуум, тогда как множество всех возможных правил вычисления функции — не более чем счётное, ведь их можно записать в виде текстов. Следовательно, далеко не для каждой такой функции можно указать правило, по которому она будет вычисляться; говорят, что одни функции вычислимы, а другие — нет.
Даже если рассматривать только функции, областью определения которых является множество натуральных чисел, а областью значений — множество десятичных цифр от 0 до 9, то и такое множество функций окажется континуумом: в самом деле, каждой такой функции можно взаимно однозначно поставить в соответствие бесконечную десятичную дробь с нулевой целой частью, взяв f(1) в качестве первой цифры, f(2) в качестве второй, f(27) в качестве двадцать седьмой и так далее, ну а множество бесконечных десятичных дробей, как мы уже видели, несчётное, то есть континуум. Ясно, что если расширить область значений до всех натуральных, то функций меньше не станет; впрочем, не станет их и “больше” — их так и останется всё тот же континуум. При этом вычислимых функций, напомним, не более чем счётная бесконечность, ведь каждой из них соответствует описание, то есть текст, а множество всех текстов счётное. Получается, что всех “натуральных” функций гораздо “больше”, нежели может существовать всех вычислимых, что бы мы ни понимали под вычислимостью — если только мы при этом подразумеваем, что правила конструктивного вычисления можно записать.
Поскольку бесконечных двоичных дробей тоже континуум, мы можем упростить множество рассматриваемых функций ещё больше, оставив лишь два варианта результата: 0 и 1, или “ложь” к “истину”. Таких функций, которые, принимая натуральный аргумент, выдают истину или ложь, тоже оказывается континуум, из чего немедленно следует, что множество всех множеств натуральных чисел тоже несчётное (имеет мощность континуум): в самом деле, ведь каждая такая функция именно что задаёт множество натуральных чисел, и, напротив, каждому множеству натуральных чисел соответствует функция, выдающая истину для элементов множества к ложь для чисел, в множество не входящих. Этот результат нам в дальнейшем изложении не потребуется, но он настолько красив, что не упомянуть его было бы варварством.
Компьютер проводит свои вычисления, подчиняясь программе, которая воплощает собой некую конструктивную процедуру, или алгоритм. Попросту говоря, для того, чтобы компьютер был нам чем-то полезен — а полезен он может быть только созданием одной информации из другой — обязательно нужен кто-то, кто точно знает, как из этой “одной” информации получить “другую”, и знает это настолько хорошо, что может заставить компьютер воплотить это знание на практике, причём без непосредственного контроля со стороны обладателя исходного знания; этот человек, собственно говоря, называется программистом. Как несложно догадаться, алгоритм как раз и есть то самое правило, по которому вычисляется функция; можно сказать, что функцию следует считать вычислимой, если для неё существует алгоритм вычисления.
Простота этих рассуждений на самом деле обманчива; понятия алгоритма и вычислимой функции оказываются материей крайне заковыристой. Так, практически в любом школьном учебнике информатики вы найдёте определение алгоритма — не пояснение, о чём идёт речь, не рассказ о предмете, а именно определение, короткую фразу вида “алгоритм — это то-то и то-то” или “алгоритмом называется то- то и то-то”. Такое определение обычно выделяется крупным жирным шрифтом, обводится рамочкой, снабжается какой-нибудь пиктограммой с восклицательным знаком — словом, делается всё, чтобы убедить как учеников, так и их учителей, что сие подлежит заучиванию наизусть. К сожалению, такие определения годятся только в качестве упражнения на зазубривание. На самом же деле определения алгоритма не существует, то есть какое бы “определение” ни приводилось, оно будет заведомо неверным: каждый автор, дающий такое определение, допускает фактическую ошибку уже в тот момент, когда решает начать его формулировать, и совершенно неважно, какова будет итоговая формулировка. Правильного определения не существует не в том смысле, что “определения могут быть разные” и даже не в том, что “мы сейчас не знаем точного определения, но, возможно, когда-нибудь узнаем”; напротив, мы точно знаем, что определения алгоритма нет и быть не может, потому что любое такое определение, каково бы оно ни было, выбьет основу из-под целого раздела математики — теории вычислимости.
Чтобы понять, как же так получилось, нам понадобится очередной экскурс в историю. В первой половине XX века математики заинтересовались вопросом, как среди всего теоретического многообразия математических функций выделить такие, которые человек с использованием каких бы то ни было механических или любых других приспособлений может вычислить. Начало этому положил Давид Гильберт, сформулировавший в 1900 году список нерешённых (на тот момент) математических проблем, известных как “Гильбертовы проблемы”; проблема решения произвольного диофантова уравнения, известная как десятая проблема Гильберта, позже оказалась неразрешимой, но для доказательства этого факта потребовалось создать теорию, формализующую понятие “разрешимости”: без этого невозможно ничего определённого сказать ни про множество задач, которые можно конструктивно решить, ни про то, что следует понимать под конструктивностью решения. Проблемами разрешимости задач (иначе говоря, вычислимости функций) занимались такие известные математики, как Курт Гёдель, Стивен Клини, Алонсо Чёрч и Алан Тьюринг.
Функции, оперирующие с иррациональными числами, пришлось отбросить сразу же. Иррациональных оказалось “слишком много”; в предыдущем параграфе мы дали некоторые пояснения, почему континуальные бесконечности не годятся для конструктивной работы.
Коль скоро континуальные бесконечности конструктивным вычислениям не поддаются, ограничивая нас счётными множествами, Гёдель и Клини предложили для теоретических изысканий рассматривать только функции натуральных аргументов (возможно, нескольких), значениями которых тоже являются натуральные числа; при необходимости любые функции, работающие над произвольными счётными множествами (в том числе, что важно для нас, и над множеством А*), могут быть сведены к таким “натуральным” функциям путём замены элементов множеств их номерами.
Здравый смысл подсказывает, что даже такие функции не всегда вычислимы; отсылка к здравому смыслу здесь требуется, поскольку мы пока не поняли (а на самом деле — так и не поймём), что же такое “вычислимая функция”. Тем не менее, как уже было сказано, функций вида N → N (где N — множество натуральных чисел) — континуум, тогда как алгоритмов, судя по всему, не более чем счётное множество; общее количество возможных функций, даже когда мы рассматриваем “всего лишь” натуральные функции натурального аргумента, оказывается “гораздо больше”, чем количество функций, которые можно как-то вычислять.
Изучая вычислимость функций, Гёдель, Клини, Аккерман и другие математики пришли к классу так называемых частично-рекурсивных функций. В качестве определения этого класса рассматривается некий базовый набор очень простых исходных функций (константа, увеличение на единицу и проекция — функция нескольких аргументов, значением которой является один из её аргументов) и операторов, то есть операций над функциями, позволяющих строить новые функции (операторы композиции, примитивной рекурсии и минимизации); под частично-рекурсивной функцией понимается любая функция, которую можно построить с помощью перечисленных операторов из перечисленных исходных функций. Слово “частичные” в названии класса указывает на то, что в этот класс обязательно41 входят функции, которые определены лишь на некотором множестве чисел, а для чисел, не входящих в это множество — не определены, то есть не могут быть вычислены. Следует отметить, что эпитет “рекурсивные” в данном контексте означает, что функции выражаются одна через другую — возможно, даже через саму себя, но не обязательно. Как мы увидим позже, в программировании смысл термина “рекурсия” несколько уже.
Многочисленные попытки расширить множество вычислимых функций путём введения новых операций успехом не увенчались: каждый раз удавалось доказать, что класс функций, задаваемых новыми наборами операций, оказывается всё тем же — уже известным классом частично-рекурсивных функций, а все новые операции благополучно (хотя в некоторых случаях довольно сложно) выражаются через уже имеющиеся.
Алонсо Чёрч отказался от дальнейших попыток расширить этот класс и заявил, что, по-видимому, как раз частично-рекурсивные функции соответствуют понятию вычислимой функции в любом разумном понимании вычислимости. Это утверждение называют тезисом Чёрча. Отметим, что тезис Чёрча не может рассматриваться как теорема — его нельзя доказать, поскольку у нас нет определения вычислимой функции и тем более нет определения “разумного понимания”. Но почему бы, спросите вы, не дать какое-нибудь определение, чтобы тезис Чёрча оказался доказуем? Ответ здесь очень простой. Превратив тезис Чёрча в якобы доказанный факт, мы совершенно безосновательно лишили бы себя перспектив дальнейшего исследования вычислимости и разнообразных механизмов вычисления.
Пока что все попытки создания набора конструктивных операций, более богатого, нежели предложенный ранее, потерпели неудачу: каждый раз оказывается, что класс функций получается ровно тот же. Вполне возможно, что так будет всегда, то есть класс вычислимых функций никогда не будет расширен; именно это и утверждает тезис Чёрча. Но ведь это не может быть доказано — хотя бы потому, что не вполне понятно, что же такое “конструктивная операция” и каково их множество. Следовательно, всегда остаётся возможность, что в будущем кто-нибудь предложит такой набор операций, который окажется мощнее, нежели базис для частично-рекурсивных функций. Тезис Чёрча в этом случае будет опровергнут, или, точнее говоря, вместо него появится новый тезис, аналогичный имеющемуся, но ссылающийся на другой класс функций. Подчеркнём, что определение вычислимой функции от этого не появится, поскольку даже если класс вычислимых функций окажется расширен, само по себе это не может означать, что его нельзя расширить ещё больше.
С некоторой натяжкой можно считать, что класс частично-рекурсивных функций со всеми его свойствами представляет собой некую абстрактную математическую теорию наподобие геометрии Евклида или, скажем, теории вероятности, тогда как понятие вычислимости как таковое находится вне математики, являясь свойством нашей Вселенной (“реального мира”) наряду со скоростью света, законом всемирного тяготения к тому подобным. Тезис Чёрча в этом случае оказывается своего рода научной гипотезой относительно того, как устроен реальный мир; всё окончательно встаёт на свои места, если мы вспомним, что согласно теории научного знания, сформулированной Карлом Поппером, гипотезы не бывают верными, а бывают только неопровергнутыми, и исследователь обязан принимать во внимание, что любая гипотеза, сколько бы подтверждений ей не нашлось, может оказаться опровергнута в будущем. Тезис Чёрча утверждает, что любая функция, которая может быть конструктивно вычислена, находится в классе частично-рекурсивных функций; это утверждение пока никому не удалось опровергнуть, в связи с чем мы принимаем его за верное. Заметим, критерий фальсификации Поппера к тезису Чёрча прекрасно применим. В самом деле, мы можем (и достаточно легко) указать такой эксперимент, положительный результат которого опроверг бы тезис Чёрча: достаточно построить некий конструктивный автомат, который вычислял бы функцию, не входящую в класс частично-рекурсивных.
Формальная теория алгоритмов построена во многом аналогично теории вычислимости. Считается, что алгоритм есть конструктивная реализация некоего преобразования из входного слова в результирующее, причём как входное слово, так и слово-результат представляют собой конечные цепочки символов в некотором алфавите. Иначе говоря, чтобы можно было говорить об алгоритме, необходимо для начала зафиксировать какой-нибудь алфавит А, и тогда алгоритмы окажутся конструктивными реализациями всё тех же знакомых нам преобразований вида А* →А*, то есть, попросту говоря, реализациями (если угодно, конструктивными правилами вычислений) функций одного аргумента, для которых аргументом является слово из символов алфавита, и слово же является результатом вычисления. Отметим, что всё сказанное никоим образом не может считаться определением алгоритма, поскольку опирается на такие выражения, как “конструктивная реализация”, “конструктивные правила вычислений”, а сами эти “термины” остаются без определений. Продолжая аналогию, мы отмечаем, что не всякое такое преобразование может быть реализовано алгоритмом, ведь таких преобразований континуум, тогда как алгоритмов, естественно, не более чем счётное множество — ведь что бы мы ни понимали под алгоритмом, мы, во всяком случае, подразумеваем, что его можно как-то записать, то есть представить в виде конечного текста, а множество всех возможных текстов счётное. Кроме того, отметим, что было бы не вполне правильно отождествлять алгоритм с тем преобразованием, которое он выполняет, поскольку два разных алгоритма могут выполнять одно и то же преобразование; к этому вопросу мы вскоре вернёмся.
Один из основателей теории алгоритмов Алан Тьюринг предложил формальную модель автомата, известную как машина Тьюринга. Этот автомат имеет ленту, бесконечную в обе стороны, в каждой ячейке которой может быть записан символ алфавита либо ячейка может быть пустой. Вдоль ленты движется головка, которая может находиться в одном из нескольких предопределённых состояний, причём одно из этих состояний считается начальным (в нём головка находится в начале работы), а другое — заключительным (при переходе в него машина завершает работу). В зависимости от текущего состояния и от символа в текущей ячейке машина может:
• записать в текущую ячейку любой символ алфавита вместо того, который там записан сейчас, в том числе и тот же самый символ, то есть оставить содержимое ячейки без изменений;
• изменить состояние головки на любое другое, в том числе остаться в том состоянии, в котором головка находилась до этого;
• сдвинуться на одну позицию вправо, на одну позицию влево или остаться в текущей позиции.
Программа для машины Тьюринга, чаще называемая просто “машиной Тьюринга”, представляется в виде таблицы, задающей, что должна сделать машина при каждой комбинации текущего символа и текущего состояния; по горизонтали отмечают символы, по вертикали — состояния (или наоборот), а в каждой ячейке таблицы записывают три значения: новый символ, новое состояние и следующее движение (влево, вправо или остаться на месте). Перед началом работы на ленте записано входное слово; если после какого-то числа шагов машина перешла в заключительное состояние, считается, что слово, которое записано теперь на ленте, является результатом работы.
Тезис Тьюринга гласит: каково бы ни было разумное понимание алгоритма, любой алгоритм, соответствующий такому пониманию, можно реализовать в виде машины Тьюринга. Этот тезис подтверждается тем, что множество предпринятых попыток создать “более мощный” автомат потерпели неудачу: для каждого создаваемого формализма (формального автомата) удаётся указать, каким способом построить аналогичную ему машину Тьюринга. Самих таких формализмов было построено немало: это и нормальные алгоритмы Маркова, и лямбда- исчисление Чёрча, и всевозможные автоматы с регистрами, причём каждый такой “алгоритмический формализм”, будучи рассмотренным в роли конкретно определимой рабочей модели вместо “неуловимого” понятия алгоритма, оказывается в том или ином виде полезен для развития теории, а в ряде случаев — и для практического применения; существуют, в частности, языки программирования, основанные на лямбда-исчислении, а также языки, вычислительная модель которых напоминает алгоритмы Маркова. При этом для каждого такого формализма было доказано, что его можно реализовать на машине Тьюринга, а машину Тьюринга — на нём.
Тем не менее доказать тезис Тьюринга не представляется возможным, поскольку невозможно определить, что такое “разумное понимание алгоритма”; это не исключает теоретической возможности, что когда-либо в будущем тезис Тьюринга окажется опровергнут: для этого достаточно предложить некий формальный автомат, соответствующий нашему пониманию алгоритма (то есть конструктивно реализуемый), но при этом имеющий конфигурации, которые в машину Тьюринга не переводятся. То, что пока никому не удалось предложить такой автомат, формально ничего не доказывает: а вдруг кому-то повезёт больше?
Всё это весьма напоминает ситуацию с вычислимыми функциями, частично-рекурсивными функциями и тезисом Чёрча, и такое подобие не случайно. Как мы уже отмечали, все преобразования вида А* → А* путём замены элемента множества А* (то есть слова) его номером (что можно сделать, поскольку множество А* счётное) могут быть превращены в преобразования вида N → N, а путём замены номера слова самим словом — обратно. Более того, доказано, что любое преобразование, реализованное машиной Тьюринга, может быть задано в виде частично-рекурсивной функции, а любая частично-рекурсивная функция — реализована в виде машины Тьюринга.
Означает ли это, что “вычислимая функция” к “алгоритм” суть одно к то же? Формально говоря, нет, и тому есть две причины. Во-первых, оба понятия не определены, так что доказать их эквивалентность невозможно, как, впрочем, и опровергнуть её. Во-вторых, как уже говорилось, эти понятия несколько отличаются по своему наполнению: если две функции, записанные различным образом, имеют при этом одну и ту же область определения и всегда дают одинаковые значения при одинаковых аргументах, обычно считается, что речь идёт о двух записях одной к той же функции, тогда как в применении к двум алгоритмам говорят об эквивалентности двух различных алгоритмов.
Прекрасным примером таких алгоритмов будет решение известной задачи о ханойских башнях. В задаче фигурируют три стержня, на один из которых надето N плоских дисков, различающихся по размеру, в виде своеобразной пирамидки (внизу самый большой диск, сверху самый маленький). За один ход мы можем переместить один диск с одного стержня на другой, при этом если стержень пуст, на него можно поместить любой диск, но если на стержне уже имеются какие-то диски, то можно поместить только меньший диск сверху на больший, но не наоборот. Брать сразу несколько дисков нельзя, то есть перемещаем мы только один диск за ход. Задача состоит в том, чтобы за наименьшее возможное число ходов переместить все диски с одного стержня на другой, пользуясь третьим в качестве промежуточного.
Хорошо известно, что задача решается за 2N — 1 ходов, где N — количество дисков, к, больше того, хорошо известен рекурсивный42 алгоритм решения, изложенный, например, в книге Я. Перельмана “Живая математика” [5], которая вышла в 1934 году. Базисом рекурсии может служить перенос одного диска за один ход с исходного стержня на целевой, однако ещё проще в качестве базиса использовать вырожденный случай, когда задача уже решена и ничего никуда переносить не надо, то есть количество дисков, которые надо перенести, равно нулю. Если нужно переместить N дисков, то мы пользуемся своим же собственным алгоритмом (то есть рекурсивно обращаемся к нему), чтобы сначала перенести N —1 дисков с исходного стержня на промежуточный, потом переносим самый большой диск с исходного стержня на целевой, и снова обращаемся к самому себе, чтобы перенести N — 1 дисков с промежуточного стержня на целевой.
Чтобы воплотить этот алгоритм в виде программы, нужно придумать некие правила записи ходов. С этим всё довольно просто: поскольку переносится всего один диск, ход представляется в виде пары номеров стержней: с какого и на какой мы собираемся переносить очередной диск. Исходными данными для нашей программы послужит количество дисков. Тексты этой программы на Паскале и на Си мы напишем позже, когда изучим эти языки в достаточной степени; нетерпеливому читателю можем предложить посмотреть § 2.14.2, где приведено решение на Паскале, ну а за решением на Си придётся обратиться ко второму тому нашей книги.
Отметим, забегая вперёд, что рекурсивная подпрограмма, осуществляющая собственно решение задачи, на обоих языках займёт по восемь строк, включая заголовок и операторные скобки, а всё остальное, что придётся написать — это вспомогательные действия, проверяющие корректность входных данных и переводящие их из текстового представления в числовое.
Рассмотрим теперь другое решение той же задачи, обходящееся без рекурсии. Перельман этого решения не привёл, так что его никто в итоге не знает43; при этом на русском языке решение описывается гораздо проще, чем рекурсивное. Итак, на нечётных ходах (на первом, третьем, пятом и т. д.) самый маленький диск (то есть диск № 1) перемещается “по кругу”: с первого стержня на второй, со второго на третий, с третьего на первый и так далее, либо, наоборот, со первого на третий, с третьего на второй, со второго на первый и так далее. Выбор “направления” этого перемещения зависит от общего количества дисков: если оно чётное, идём в “естественном” направлении, то есть 1 → 2 → 3 → 1 → ..., если же оно нечётное, идём “обратным” кругом: 1 → 3 → 2 → 1 → .... Перенос диска на чётных ходах определяется однозначно тем, что мы не должны при этом трогать самый маленький диск, а сделать ход, не трогая его, можно только одним способом, то есть мы попросту смотрим на те два стержня, на которых нет самого маленького диска, к делаем единственный возможный ход между ними.
Как ни странно, компьютерная программа, воплощающая этот вариант решения головоломки, оказывается значительно (более чем в десять раз!) сложнее, чем вышеприведённая для рекурсивного случая. Дело тут в формальной реализации фразы “смотрим на два стержня и делаем единственный ход”. Человек, решая головоломку, действительно посмотрит на стержни, сравнит, какой из верхних дисков меньше, и перенесёт этот диск. Чтобы сделать то же самое в программе, нам придётся запоминать, какие диски на каком стержне в настоящий момент присутствуют, что не слишком сложно, если уметь работать с односвязными списками, но всё же достаточно сложно, чтобы не вставлять текст этой программы в книгу — во всяком случае, целиком. Рекурсивное решение оказалось таким простым, потому что мы не помнили, какие диски где присутствуют, мы и без этого знали, какие ходы надо сделать.
Что можно сказать точно, так это то, что при тех же входных данных эта программа напечатает такие же ходы, как и предыдущая (рекурсивная), хотя сама программа, очевидно, будет написана совершенно иначе. Терминологическая проблема, встающая в этот момент, следующая. Очевидно, что речь идёт о двух разных программах (такие программы называются эквивалентными). Но идёт ли речь о двух разных алгоритмах или об одном и том же, записанном разными словами? В большинстве случаев принимается “очевидный” ответ, что это два разных алгоритма, пусть и эквивалентных, то есть реализующих одну и ту же функцию (естественно, вычислимую).
Тем не менее, обычно считается, что в теории алгоритмов и в теории вычислимых функций речь идёт более-менее об одном и том же. Здравый смысл подсказывает, что это правильно: и то, и другое представляет собой некое “конструктивное” преобразование из некоторого счётного множества в него же само, только множества рассматриваются разные: в одном случае это множество цепочек над неким алфавитом, в другом случае — просто множество натуральных чисел. Нумерация цепочек позволяет легко переходить от одного к другому, не нарушая “конструктивности”, чем бы она ни была; следовательно, мы имеем дело с одной и той же сущностью, только выраженной в разных терминах. Различать ли преобразования только с точностью до их “внешних проявлений”, как в теории вычислимости, или же с точностью до их “конкретного воплощения”, как в теории алгоритмов — это, в конце концов, вопрос традиций. Более того, у многих авторов встречается понятие “тезиса Чёрча-Тьюринга”, предполагающее, что эти тезисы не следует разделять: речь ведь идёт об одном и том же, только в разных терминах.
После всего сказанного любые определения алгоритма вызывают в лучшем случае недоумение, ведь дав такое определение, мы тем самым отправим на свалку теорию вычислимости и теорию алгоритмов, тезис Чёрча вместе с тезисом Тьюринга, множественные попытки построения чего-то более сложного — например, машины Тьюринга с несколькими лентами, доказательства их эквивалентности исходной машине Тьюринга, работу сотен, возможно даже тысяч исследователей — а определение при этом всё равно окажется либо неправильным, либо настолько расплывчатым, что его невозможно будет использовать на практике.
Значит ли это, что понятие алгоритма вообще нельзя использовать из-за его неопределённости? Конечно же, нет. Во-первых, если говорить о математике, то мы вообще довольно часто используем понятия, не имеющие определений: например, нельзя дать определения точки, прямой и плоскости, но этот факт никоим образом не отменяет геометрию. Во-вторых, если говорить о сфере инженерно-технических знаний, то строгие определения здесь вообще встречаются очень редко, и это никому не мешает. Наконец, следует принять во внимание тезисы Чёрча и Тьюринга: с учётом этих тезисов понятие алгоритма обретает вполне строгое математическое наполнение, нужно только помнить, откуда это наполнение взялось, то есть не забывать о роли тезисов Чёрча и Тьюринга во всей нашей теории.
1.5.6. Алгоритм и его свойства
Несмотря на то, что само понятие алгоритма не может быть определено, наше интуитивное понимание алгоритма позволяет говорить о некоторых свойствах, выполняющихся для любого объекта, который нам может прийти в голову считать алгоритмом. Кроме того, можно говорить о неких характеристиках алгоритмов, то есть о свойствах, которые могут выполняться для одних алгоритмов и не выполняться для других.
Одно из базовых свойств любого алгоритма мы уже неоднократно использовали в наших рассуждениях, постулируя, что алгоритм можно записать в виде текста, притом, естественно, конечного: бесконечные тексты мы в действительности записать не можем сугубо технически, так что, коль скоро алгоритмы имеют отношение к конструктивной деятельности, бесконечными они быть не могут. Представимость любого алгоритма в виде текста, и притом конечного, можно назвать свойствами объективности и конечности алгоритма.
Ещё одно достаточно очевидное свойство любого алгоритма — его дискретность: каково бы ни было правило, согласно которому из исходной информации получают результирующую, и каков бы ни был исполнитель этого правила, само по себе исполнение всегда представляет собой некий дискретный процесс, который при ближайшем рассмотрении распадается на какие-то элементарные шаги/действия. Понимать дискретность можно также и в том смысле, что любая информация, над которой работает алгоритм, может быть представлена в виде текста, что означает, в частности, что с целыми и рациональными числами мы работать можем, а с иррациональными у нас возникнут определённые сложности. Впрочем, коль скоро для иррационального числа существует обозначение, алгоритм вполне может оперировать таким числом — точнее, не им самим, а его обозначением; так, мы вполне можем придумать такой алгоритм для решения квадратных уравнений, который при невозможности извлечения квадратного корня из дискриминанта выдаст в качестве результата выражение, содержащее этот корень: например, получив на вход уравнение х2 — 5х + 6 = 0, такой алгоритм в качестве результата выдаст числа 2 и 3, тогда как для уравнения х2 — х — 1 =0 он, используя то или иное текстовое обозначение квадратного корня, выдаст в качестве ответа выражения ![]() Важно понимать, что такой алгоритм ни в какой момент не будет оперировать численным значением √5, поскольку таковое не имеет дискретного представления.
Важно понимать, что такой алгоритм ни в какой момент не будет оперировать численным значением √5, поскольку таковое не имеет дискретного представления.
Заметим, что число √5 имеет довольно простое “аналоговое” представление: достаточно зафиксировать некий эталон единичной длины, например, сантиметра, к взять прямоугольник со сторонами 1 к 2, к его диагональ как раз будет представлять корень из пяти. Иначе говоря, мы можем построить (если угодно, с помощью циркуля и линейки) отрезок, который будет ровно в √5 раз длиннее заданного. Если немного подумать, можно, используя исходно целые величины, получить √5 в виде силы, действующей на какое-нибудь тело, в виде объёма жидкости в сосуде и тому подобных аналоговых физических величин. Так вот, алгоритмы ни с чем подобным не работают; как мы уже говорили, вся теория вычислимости построена исключительно на целых числах, и целыми же (в конечном счёте) числами оперируют компьютеры.
В принципе, известны так называемые аналоговые ЭВМ, работающие как раз с непрерывными физическими процессами; исходные, промежуточные и результирующие данные в таких машинах представляются значениями электрических величин, чаще всего напряжения; но функционирование аналоговых ЭВМ не имеет ничего общего с алгоритмами.
Третье фундаментальное свойство, присущее любому алгоритму, не столь очевидно; оно называется детерминированностью и состоит в том, что алгоритм не оставляет исполнителю никакой “свободы выбора”: следовать предписанной процедуре можно одним и только одним способом. Единственное, что может повлиять на ход выполнения алгоритма — это исходные данные; в частности, при одних и тех же исходных данных алгоритм всегда выдаёт одни и те же результаты.
Читатели, уже сталкивавшиеся с практическим программированием, могут заметить, что программы, в особенности игровые (а также, например, криптографические), часто отходят от этого правила, используя датчики случайных чисел. На самом деле это никоим образом не противоречит теории алгоритмов, просто случайные числа, откуда бы они ни брались, следует рассматривать как составную часть исходных данных.
Свойства объективности/конечности (в том смысле, что всякий алгоритм имеет конечное объективное представление), дискретности и детерминированности присущи всем алгоритмам без исключения, то есть если нечто не обладает каким-либо из этих свойств, то перед нами заведомо никакой не алгоритм. Конечно, эти свойства следует рассматривать скорее, как некие аксиомы, то есть утверждения, которые приняты, невзирая на их недоказуемость: просто принято считать, что алгоритмы, что бы под ними ни понималось, всегда таковы. С некоторой натяжкой можно утверждать, что алгоритм должен ещё обладать понятностью для исполнителя, хотя это уже на грани фола: понятность относится скорее не к алгоритму, а к его записи, но ведь алгоритм и его запись — это совсем не одно и то же; больше того, один алгоритм может иметь бесконечно много представлений даже в одной и той же системе записи: например, если в программе переименовать все переменные или поменять местами подпрограммы, алгоритм от этого не изменится.
Наряду с перечисленными обязательными свойствами алгоритм может обладать (но может и не обладать) некоторыми частными свойствами, такими как массовость, завершаемость (применимость к отдельным входным словам или ко всем возможным входным словам), правильность и полезность (что бы под ними ни понималось) и т. д. Возможно, эти свойства желательны, но не более того; это характеристики, которым отдельно взятый алгоритм может соответствовать, а может и не соответствовать, а во многих случаях такое соответствие даже нельзя (невозможно!) проверить. К сожалению, существует много разнообразных литературных источников сомнительного качества (в число которых, как ни прискорбно, входят некоторые школьные учебники информатики), где обязательные свойства алгоритмов сваливают в одну кучу с частными, порождая на выходе совершенно феерический кавардак.
Начнём со свойства массовости алгоритма, как самого простого; это свойство обычно понимается в том смысле, что алгоритм должен уметь решать некое семейство задач, а не одну задачу; именно для этого алгоритм делают зависимым от входных данных. Свойство массовости, очевидно, можно проверить, то есть, рассматривая конкретный алгоритм, легко определить, обладает он массовостью или нет; но на этом, собственно, и всё. Обязательным оно никоим образом не является, то есть алгоритм, который вообще не зависит от входных слов, алгоритмом быть не перестаёт. Как среди вычислимых функций присутствуют константы, так и среди алгоритмов присутствуют генераторы единственного результата. Между прочим, именно к этой категории относится знаменитая программа “Hello, world” — излюбленный многими авторами пример первой программы на очередном языке программирования; всё, что она делает — это выдаёт фразу “Hello, world!”44и завершается. Кстати, мы тоже начнём изучение Паскаля, а затем и Си именно с этой программы. Очевидно, программа, всегда печатающая одну и ту же фразу, вообще никак не зависит ни от каких входных данных и, следовательно, никакой массовостью не обладает. Если бы мы считали массовость обязательным свойством алгоритма, пришлось бы считать, что программы, подобные этой, не реализуют никаких алгоритмов.
Если, скажем, рассматривать обыкновенные треугольники на плоскости, то можно заметить, что всякий треугольник подчиняется неравенству треугольника (то есть сумма длин любых двух сторон заведомо больше длины третьей стороны), а ещё его сумма углов всегда равна 180°; это свойства всех треугольников без исключения. Кроме того, среди всех треугольников есть ещё прямоугольные треугольники, для которых выполняется теорема Пифагора; разумеется, теорема Пифагора — очень важное к нужное свойство, но было бы нелепо требовать её выполнения для всех треугольников. Именно так обстоят дела к с массовостью алгоритмов.
Когда в рассуждениях о свойствах алгоритмов не проводится явной границы между свойствами обязательными, то есть присущими всем алгоритмам без исключения, и свойствами частными, такими, которыми алгоритм может обладать или не обладать, результатом таких рассуждений становятся грубейшие фактические ошибки; сейчас мы постараемся обсудить наиболее популярные из них. Такое обсуждение позволит нам, во-первых, не повторять ошибок, чья популярность никоим образом не отменяет их грубости, и, во-вторых, по ходу обсуждения мы узнаем ещё несколько интересных аспектов теории алгоритмов.
Так, на удивление часто можно встретить утверждение, что любой алгоритм должен обладать свойствами “правильности” и “завершаемости”, то есть, иначе говоря, любой алгоритм якобы должен всегда завершаться за конечное число шагов, притом не просто завершаться, а выдавать при этом правильный результат. Конечно, хотелось бы, чтобы все алгоритмы (и, стало быть, все компьютерные программы) действительно никогда не зависали и не делали никаких ошибок; как говорится, хотеть не вредно. В реальности дела обстоят совершенно иначе: такое “райски-идеальное” положение вещей оказывается принципиально недостижимо, причём не только технически, но и, как мы вскоре увидим, сугубо математически. С таким же успехом можно было бы хотеть, чтобы все автомобили были оснащены вечными двигателями, а число π стало равно трём, чтобы легче было считать.
Начнём с “правильности”. Очевидно, что это понятие попросту невозможно формализовать; более того, зачастую при разработке алгоритма вообще невозможно указать какой бы то ни было критерий проверки “правильности”, или, что ещё хуже, разные люди могут оперировать разными критериями при оценивании одного и того же алгоритма. Это свойство предметной области хорошо известно профессиональным программистам: одно и то же поведение компьютерной программы может её автору казаться правильным, а заказчику — не просто неправильным, но даже в некоторых случаях возмутительным. Никакие формальные описания, никакое сколь угодно подробное тестирование не способны эту ситуацию исправить. Среди программистов небезосновательно считается, что “правильных” программ не бывает, бывают лишь такие программы, в которых пока не найдено ошибок — но это не значит, что ошибок там нет. Некоторое время назад среди программистов-исследователей была популярна тема формальной верификации программ, доказательного программирования и т. п.; никаких обнадёживающих результатов в этой области никто так и не достиг, и популярность направления пошла на убыль. Получается, что если считать правильность обязательным свойством любого алгоритма, из этого будет следовать, что алгоритмов не существует — во всяком случае, их нельзя “предъявить”, ведь проверить свойство “правильности” технически невозможно.
Со свойством “завершаемости” дела обстоят ещё интереснее. В теории алгоритмов имеется термин “применимость”: алгоритм называется применимым к данному входному слову, если, имея это слово на входе, алгоритм завершается за конечное число шагов. А теперь самое интересное: проблема применимости алгоритма к входному слову является алгоритмически неразрешимой, то есть невозможно — математически! — построить такой алгоритм, который, получив на вход запись другого алгоритма и некоторое входное слово, определил бы, применим данный алгоритм к данному слову или нет. Проблема применимости, известная также под названием проблема останова, является хрестоматийным примером алгоритмически неразрешимой проблемы.
Неразрешимость проблемы применимости можно доказать, как говорится, в три строчки, если привлечь её частный случай — проблему самоприменимости, то есть вопрос о том, остановится ли данный алгоритм, если на вход ему подать его собственную запись. В самом деле, допустим, такой алгоритм есть; назовём его S. Напишем алгоритм S' следующего вида45:
![]()
Ясно, что алгоритм S' может быть либо самоприменим, либо не самоприменим. Рассмотрим его применение к самому себе, то есть S'(S'). Предположим, S' самоприменим; тогда результатом S(S') будет истина, и, следовательно, S'(S') в соответствии с собственным определением уйдёт в бесконечный цикл, то есть окажется не применим к самому себе, что противоречит предположению. Предположим теперь, что алгоритм S' не является самоприменимым. Тогда результатом S(S') будет ложь, так что S'(S') благополучно завершится, то есть окажется самоприменим, что, опять-таки, противоречит предположению. Таким образом, алгоритм S' не является ни самоприменимым, ни несамоприменимым; следовательно, его попросту не существует. Как следствие, не существует к алгоритма S, иначе S' можно было бы написать (вне зависимости от того, какой из алгоритмических формализмов мы используем — и ветвление, и бесконечный цикл реализуются везде).
Вернёмся к свойству “завершаемости”. Обычно при его упоминании никакой речи о “входных словах” не идёт, то есть авторы, приписывающие алгоритму такое свойство, имеют в виду, по всей видимости, что алгоритм должен быть, следуя классической терминологии, применим к любому входному слову. Между тем, на самом деле невозможно (в общем случае) проверить даже применимость алгоритма к одному отдельно взятому входному слову, не говоря уже обо всём бесконечном множестве таких слов. Конечно, можно указать тривиальные случаи таких алгоритмов: например, алгоритм, всегда выдающий одно и то же значение вне зависимости от входного слова, будет заведомо применим к любому входному слову. Однако не только “в общем случае”, но и во всех мало-мальски “интересных” случаях, к каковым относятся практически любые полезные компьютерные программы, мы не можем сказать ничего определённого на тему “завершаемости”: алгоритмическая неразрешимость — штука упрямая. Если считать “завершаемость” априорным свойством любого алгоритма (то есть считать, что нечто, не обладающее этим свойством, алгоритмом не является), то мы вообще не сможем привести примеры алгоритмов, за исключением самых тривиальных, и уж точно упустим из рассмотрения большую и наиболее интересную часть алгоритмов. Иначе говоря, если включить “завершаемость” в понятие алгоритма, как это, увы, часто делают авторы учебников, мы с таким понятием “алгоритма” в подавляющем большинстве случаев не смогли бы вообще определённо сказать, алгоритм перед нами или нет, то есть попросту не смогли бы отличать алгоритмы от не-алгоритмов; зачем нам, спрашивается, тогда такое определение?
Ситуация начинает выглядеть ещё пикантнее, если учесть, что в теории вычислимых функций возможная неопределённость функции на подмножестве области её определения играет чрезвычайно важную роль, причём любые попытки доопределить функции вроде “рассмотрим другую функцию, которая равна нулю во всех точках, в которых исходная функция не определена” терпят сокрушительное фиаско.
Чтобы понять, почему это так, рассмотрим следующее довольно простое рассуждение. Поскольку мы договорились, что любые конструктивные вычисления можно записать в виде текста, из этого следует, что вычислимых функций — счётное множество, то есть существует некоторая нумерация всех вычислимых функций. Пусть теперь мы пытаемся ввести такое понятие вычислимой функции одного аргумента, что всякая функция, вычислимая в этом смысле, оказывается при этом определена на всём множестве натуральных аргументов. Ясно, что, поскольку речь идёт о вычислимых функциях, этих функций тоже не более чем счётное множество. Обозначим их все через f1, f2, f3, ..., fn, ...; иначе говоря, пусть нумерованная последовательность fn исчерпывает множество вычислимых (в нашем смысле) функций. Рассмотрим теперь функцию g(n) = fn(n) + 1. Ясно, что в любом разумном смысле такая функция вычислима, но в то же время она отличается от каждой из fn, то есть получается, что она в множество вычислимых функций не входит46.
Как следствие, мы должны либо согласиться с тем, что прибавление единицы может сделать из вычислимой функции невычислимую, либо принять как данность, что при рассмотрении вычислимых функций (что бы мы под таковыми ни понимали) ограничиваться только всюду определёнными функциями нельзя. Заметим, если функции семейства fn не обязаны быть всюду определёнными, то никакого противоречия у нас не возникает; в самом деле, если функция fk не определена в точке k, то g(n), определённая вышеуказанным способом, оказывается тоже не определена в точке k, и, как следствие, её отличие от каждой из fk более не гарантируется её определением; иначе говоря, g(n) может совпадать с любой из тех функций fk, которые не определены в точке, соответствующей их номеру, и, соответственно, “получает право” не выходить за пределы множества {fk}.
Интересно, что в теории вычислимых функций рассматривается некий “упрощённый” класс функций — так называемые примитивно-рекурсивные функции. От частично-рекурсивных функций их отличает отсутствие оператора минимизации, то есть функции строятся на основе тех же примитивных функций (константы, увеличения на единицу и проекции) и операторов суперпозиции и примитивной рекурсии. Все функции, построенные таким образом, заведомо определены для любых значений аргументов, “зацикливаться” им попросту негде; в классе частично-рекурсивных функций возможность “неопределённости” вносит как раз оператор минимизации.
Казалось бы, класс этот достаточно широк, причём, если говорить об арифметике целых чисел, складывается (обманчивое) впечатление, что он покрывает “почти всё”. Чтобы привести пример частично-рекурсивной функции, которая не была бы при этом примитивно-рекурсивной, Вильгельму Аккерману пришлось специально придумать функцию, которую потом так и назвали функцией Аккермана; эта функция двух аргументов растёт настолько стремительно, что все её осмысленные значения умещаются в небольшую табличку, за пределами которой эти числа превышают количество атомов во Вселенной.
Если, однако, из области целочисленных функций вернуться в привычный нам мир алгоритмов, выяснится, что, когда речь идёт о нумерации входных и выходных цепочек, количество атомов во Вселенной окажется не таким уж и большим числом, примером же функции, которая, будучи частично-рекурсивной, не является примитивно-рекурсивной, “внезапно” оказывается любая компьютерная программа, использующая “неарифметические” циклы, то есть, по сути, обыкновенные циклы while, для которых на момент входа в цикл нельзя (иначе как пройдя цикл) определить, сколько будет у этого цикла итераций. Точно также оказывается “непримитивной” программа, использующая рекурсию, для которой при входе нельзя заранее узнать, сколько получится уровней вложенности47.
Для человека, имеющего опыт написания компьютерных программ, оказываются довольно очевидными два момента. С одной стороны, если программу писать только с использованием арифметических циклов, таких как for в Паскале, к при этом без всякой рекурсии (или с использованием “примитивной” рекурсии, для которой количество вложенных вызовов не превышает заданного числа), то можно будет заранее оценить (сверху) время выполнения такой программы. Зацикливаться таким программам попросту негде, так что какие бы данные ни оказались на входе, за конечное число шагов такая программа заведомо завершится.
С другой стороны, увы, ни одной мало-мальски полезной программы так не написать. Как только мы пытаемся решить практическую задачу, нам приходится прибегнуть либо к циклу while, либо к рекурсии без “счётчика уровней”, либо к оператору перехода назад (каковой на самом деле тоже представляет собой цикл while, так что вместо такого перехода как раз и следует использовать цикл). Ну а вместе с таким “недетерминированным повторением” в нашу программу просачиваются источники неопределённостей, алгоритмическая неразрешимость вопроса об останове и прочие прелести, известные пользователям под общим названием “глюки”. При взгляде на действительность под таким углом оказывается, что общая “глючность” программ является не следствием безалаберности программистов, как это принято считать, а скорее математическим свойством предметной области. А всё потому, что, добавив в свою программу хотя бы одно недетерминированное повторение (будь то неарифметический цикл или непримитивная рекурсия), мы тем самым выводим алгоритм, реализуемый нашей программой, из класса примитивно-рекурсивных функций в класс частичнорекурсивных.
Таким образом, неопределённость некоторых вычислимых функций в некоторых точках, или, что то же самое, неприменимость некоторых алгоритмов к некоторым входным словам — это фундаментальное свойство любых моделей конструктивных вычислений, практически тривиально вытекающее из самых основ теории. С этим не только нельзя ничего сделать, но и не нужно ничего делать, иначе мы потеряем гораздо больше, чем приобретём: наши программы станут “правильными” и совершенно перестанут “глючить”, только при этом они ещё и станут бесполезны.
1.5.7. Последовательность действий тут ни при чём
Среди “определений” алгоритма, которые, несмотря на их изначальную некорректность, всё же встречаются в литературе, и притом гораздо чаще, чем хотелось бы, преобладают вариации на тему “последовательности действий”. Так вот, в действительности алгоритм в общем случае может не иметь ничего общего ни с какими последовательностями действий, во всяком случае, явно описанными.
В самом деле, мы уже упоминали, что для изучения алгоритмов используют самые разные формальные системы: среди них, например, машина Тьюринга (представляемая таблицей перехода между состояниями) и частичные рекурсивные функции (представляемые комбинацией базовых функций и операторов). Отметим, что в число алгоритмических формализмов входят также нормальные алгоритмы Маркова (набор правил по переписыванию слова, находящегося в поле зрения), лямбда-исчисление (системы функций одного аргумента над неким пространством выражений), абстрактная машина с неограниченными регистрами (МНР) и многие другие модели. Последовательность действий, выписанная в явном виде, среди всех этих формализмов присуща только МНР; между тем многократно доказано, что все эти формализмы попарно эквивалентны, то есть задают один и тот же класс возможных вычислений. Иначе говоря, любой алгоритм может быть представлен в любой из имеющихся формальных систем, среди которых большинство не имеет ничего общего с последовательностями действий.
Если вернуться с математических небес на грешную программистскую землю, мы обнаружим, что к воплощение алгоритма в виде компьютерной программы далеко не всегда будет описанием последовательности действий. Здесь всё зависит от используемой парадигмы программирования, то есть от стиля мышления, используемого программистом; во многом этот стиль определяется языком программирования. Так, при работе на языке Haskell и других языках функционального программирования у нас вообще нет никаких действий, есть лишь функции в сугубо математическом смысле — функции, вычисляющие некоторое значение на основе заданных аргументов. Вычисление такой функции выражается через другие функции, и это выражение не имеет ничего общего с действиями и их последовательностями. В большинстве случаев для программ на Haskelle вообще невозможно предсказать, в какой последовательности будут произведены вычисления, поскольку язык реализует так называемую ленивую семантику, позволяющую отложить выполнение вычисления до тех пор, пока результат оного не потребуется для другого вычисления.
Если на Haskelle мы хотя бы задаём то, как нужно вычислять результат, пусть даже и не в виде конкретной “последовательности действий”, то при работе на языках программирования, имеющих декларативную семантику, мы вообще не обращаем внимания на то, как искать требуемое решение; мы лишь указываем, какими свойствами оно должно обладать, а то, как его найти, оставляем на усмотрение системы. Среди таких языков наиболее известен реляционный язык Пролог: программа на этом языке пишется в виде набора логических утверждений, а её исполнение представляет собой доказательство теоремы (точнее, попытку её опровержения).
Наконец, суперпопулярная ныне парадигма объектно-ориентированного программирования тоже основана не на “последовательностях действий”, а на некоем обмене сообщениями между абстрактными объектами. Если же говорить о последовательностях действий, то в виде таковых программа пишется лишь на так называемых императивных языках программирования, также называемых иногда “фоннеймановскими”. К таким языкам относятся, например, Паскаль, Си, Бейсик к достаточно много других языков; однако популярность фоннеймановского стиля обусловлена исключительно господствующим подходом к построению архитектуры компьютера, а вовсе не “простотой” или тем более “естественностью” императивных конструкций.
В последние годы автору приходилось встречать утверждение, что объектно-ориентированное программирование есть якобы не более чем развитие идеи программирования императивного. Такие утверждения несостоятельны хотя бы потому, что основой императивного программирования является понятие присваивания, тогда как в каноническом ООП запрещены любые предположения о внутреннем состоянии объекта и, как следствие, операция присваивания (означающая, что состояние одного объекта должно стать копией состояния другого объекта) заведомо не может существовать. Причиной возникновения ощущения “императивной природы” ООП является исключительно то обстоятельство, что все индустриальные языки программирования, реализующие объектную парадигму, являются не чистыми объектно-ориентированными языками, а, напротив, языками императивными, имеющими ООП-надстройку; таковы и Си++, и Джава, и С#. Неудивительно, что в том же Си++ не просто можно присваивать объекты, но и присутствует специальная языковая поддержка этого; но всё это обусловлено не объектами, а исходно императивной природой языка Си++, основанного на Си.
Ясно, что программы на любом реально существующем языке программирования обладают свойством конструктивной вычислимости, иначе не могла бы существовать практическая реализация такого языка — а она существует. Очевидно, таким образом, что компьютерная программа — это всегда алгоритм, как её ни напиши; определение алгоритма как последовательности действий, следовательно, никуда не годится и может привести к достаточно опасным заблуждениям. Между прочим, в заблуждение авторы таких определений вгоняют также и самих себя: именно здесь кроется, по-видимому, источник часто встречающегося, но при этом совершенно безумного утверждения, что “языки программирования делятся на алгоритмические и неалгоритмические”. Разумеется, в действительности любой язык программирования является алгоритмическим. Можно было бы, пожалуй, представить себе некий язык программирования, не обладающий свойством детерминированности, основанный, скажем, на эвристиках и, как следствие, не гарантирующий не только правильности программ, но даже их стабильности, а результаты выполнения программ делающий совершенно непредсказуемыми. Подобного рода подходы к решению некоторых задач, как ни странно, действительно существуют (вспомнить хотя бы те же нейронные сети), но до создания таких языков программирования, к счастью, дело не дошло, да и популярность нейронных сетей давно уже сошла на нет: с непредсказуемыми результатами тяжело работать, такие методы, в частности, полностью исключают отладку, так что практический потенциал неалгоритмических вычислений весьма сомнителен.
Впрочем, говоря о “неалгоритмических” языках, обычно имеют в виду сущность гораздо более простую: именно, все языки, на которых программа записывается иначе как в виде всё той же “последовательности действий”. Строго говоря, “неалгоритмическими” тогда следовало бы, наверное, признать вообще все современные языки, кроме разве что языка ассемблера, ведь даже насквозь императивные Си и Паскаль допускают рекурсивное программирование к, как следствие, написание программы в виде, не имеющем с “последовательностью действий” ничего общего.
Отметим, что для выражения той же мысли о “делении” языков программирования можно предложить вполне корректную формулировку: например, сказать, что языки программирования делятся на императивные к неимперативные, что, конечно, потребует хотя бы краткого пояснения термина “императивное программирование”, и вот здесь как раз вполне имеет право появиться “последовательность действий”.
Защищая свою картину мира, любители определять алгоритм как последовательность действий довольно часто прибегают к утверждению, что в теории алгоритмов-де рассматривается “не тот алгоритм”, а теория вычислимости якобы вообще не имеет отношения к программированию. Как водится в таких случаях, опровергнуть такое утверждение оказывается несколько сложно — в самом деле, оно ведь при ближайшем рассмотрении оказывается сугубо терминологическим, ну а споры, центральным пунктом которых является значение того или иного термина — занятие неблагодарное.
Тем не менее, кое-что сказать на эту тему всё же можно и даже нужно. Начнём с алгоритмической неразрешимости: можно сколько угодно апеллировать к “абстрактной математичности” теории алгоритмов, но стоит предложить более-менее грамотному программисту разработать дополнение к операционной системе, которое бы само автоматически находило “зависшие” программы и останавливало бы их — и если программист что-то представляет собой в плане квалификации, мы тут же услышим, что за такую задачу он не возьмётся, да и никто не возьмётся, а если вдруг кто и возьмётся, то всё равно не решит, ведь это алгоритмически неразрешимая проблема. Получается, что в этом случае алгоритм оказался “именно тот”.
Больше того, алгоритмическая неразрешимость проблемы применимости (проблемы останова) вдохновляет программистов на быструю и эффективную отправку “в сад” любых идей, связанных с доказательством свойств произвольной программы: уж если невозможно даже формально предсказать, остановится она или нет, то что говорить о свойствах более интересных.
Несмотря на это, стоит только упомянуть теорию вычислимости или какие-нибудь термины из неё, вроде “частично-рекурсивных функций”, и у нас почему-то резко повышается риск нарваться на собеседника, утверждающего, что “это не тот алгоритм”. В принципе, это явление легко объясняется: алгоритмическую неразрешимость обычно демонстрируют, не влезая в дебри теории вычислимости и даже вообще не упоминая её, причём делается это в большинстве случаев ровно так, как сделали мы ранее. Доказательство неразрешимости проблемы самоприменимости алгоритма практически тривиально, так что у большинства будущих программистов, хотя бы раз увидевших его, не возникает никаких трудностей с постижением сути алгоритмической неразрешимости. Иное дело теория вычислимости: это предмет весьма специфический, так что большинство программистов никогда толком и не слышали термина “частично-рекурсивная функция” и уж тем более не знают, что это за зверь. Отмахнуться от непонятного, естественно, гораздо проще, нежели в него вникать.
Больше того, выше мы уже показали, что классы функций, введённые в теории вычислимости, имеют к практическому программированию самое прямое отношение, а именно, что примитивно-рекурсивные функции соответствуют классу программ без “непредсказуемых” циклов, тогда как частично-рекурсивные функции соответствуют всему множеству компьютерных программ. Найдутся ли после этого желающие утверждать, что алгоритм в математическом смысле — это “не тот” алгоритм?