Возведение в степень и деление натуральных чисел - Материалы для подготовки к самостоятельным работам

Пример 1. Вычислим:

а) 8²;

б) 5³;

в) 19¹.

Решение. Применим определение степени с натуральным показателем:

а) 8² = 8 ∙ 8 = 64;

б) 5³ = 5 ∙ 5 ∙ 5 = 25 ∙ 5 = 125;

в) 19¹ = 19.

Пример 2. Вычислим:

Решение. Деление во всех случаях можно выполнить уголком. Покажем другие способы вычисления.

а) Так как 56 : 7 = 8, а 560 в 10 раз больше, чем 56, то 560 : 7 = 80 (здесь и далее деление легко проверить умножением).

б) Воспользуемся свойством частного, разделим делимое и делитель на 10, потом на 11, получим 5500 : 220 = 550 : 22 = 50 : 2 = 25.

в) Так как число 3987 сначала умножили, а потом разделили на одно и то же число 11, то получили то же число 3987. Для проверки можно умножить частное 3987 на делитель 11 — получится делимое 3987 ∙ 11.

Замечание. Задания г) — е) можно выполнить, используя свойство частного: (а + b) : с = а : с + b : с.

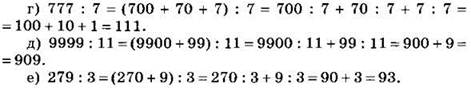
Пример 3. Число 26 увеличили в 10 раз, полученный результат уменьшили в 2 раза. Какое число получили?

Решение.

1) 26 ∙ 10 = 260 — получили после увеличения числа 26 в 10 раз;

2) 260 : 2 = 130 — получили после уменьшения 260 в 2 раза.

Ответ. 130.

Пример 4. Задумали число, увеличили его в 7 раз, полученный результат уменьшили в 5 раз и получили 42. Какое число задумали?

Решение. Воспользуемся схемой (рис. 3). Решим задачу обратным ходом:

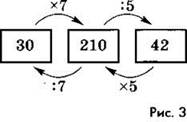
1) 42 ∙ 5 = 210;

2) 210 : 7 = 30.

Ответ. 30.

Пример 5. Число 5 возвели в степень 2, полученный результат возвели в степень 3. В какую степень за два раза возвели число 5?

Решение. Число 5 возвели в степень 2, получили 5² = 5 ∙ 5. Число 5 ∙ 5 возвели в степень 3, получили

Ответ. 6.