Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Умножение и деление степеней - СТЕПЕНЬ И ЕЕ СВОЙСТВА - СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Цель: рассмотреть свойства умножения и деления степеней с одинаковыми основаниями.
Планируемые результаты: научиться умножать и делить степени с одинаковыми основаниями.
Тип уроков: уроки общеметодологической направленности.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Дайте определение степени с натуральным показателем.
2. Какое число получается при возведении положительного числа в степень?
3. Выполните возведение в степень:
![]()
4. Выполните действие:
а) (12 - 3)2;
б) 122 - 32.
5. Запишите в виде выражения куб суммы чисел а и b.
Вариант 2
1. Дайте определение степени с натуральным показателем.
2. Какое число получается при возведении отрицательного числа в степень?
3. Выполните возведение в степень:
![]()
4. Выполните действие:
а) (14 - 5)2;
б) 142 - 52.
5. Запишите в виде выражения сумму кубов чисел а и b.
III. Работа по теме уроков
При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются, т. е. ![]()
Используя определение степени с натуральным показателем и свойства умножения, получаем
![]()
Доказанное свойство выполняется для любого числа множителей.
Пример 1
![]()
При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются, т. е. ![]() . Очевидно, что а ≠ 0 (так как делить на нуль нельзя) и m > n (степень m - n должна также быть натуральным числом).
. Очевидно, что а ≠ 0 (так как делить на нуль нельзя) и m > n (степень m - n должна также быть натуральным числом).
Очевидно, что равенство ![]() будет доказано, если будет доказано, что произведение аm-n и аn равно аm. Используя свойство умножения степеней, получаем
будет доказано, если будет доказано, что произведение аm-n и аn равно аm. Используя свойство умножения степеней, получаем ![]()
![]() Тогда пo определению частного имеем
Тогда пo определению частного имеем ![]() .
.
Пример 2
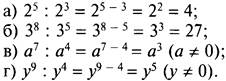
Свойство деления ![]() было доказано для случая m - n > 0. Будем считать, что такое же свойство справедливо и при m = n. Тогда получаем
было доказано для случая m - n > 0. Будем считать, что такое же свойство справедливо и при m = n. Тогда получаем ![]() Очевидно, что при a ≠ 0 и любом натуральном m величина
Очевидно, что при a ≠ 0 и любом натуральном m величина ![]() Поэтому разумно считать, что а0 = 1 при а ≠ 0. Итак, степень числа а, не равного нулю, с нулевым показателем равна единице, т. е. а0 = 1 при а ≠ 0. Заметим, что если основание равно нулю, то степень с нулевым показателем не определена (не имеет смысла), т. е. 00 не имеет смысла.
Поэтому разумно считать, что а0 = 1 при а ≠ 0. Итак, степень числа а, не равного нулю, с нулевым показателем равна единице, т. е. а0 = 1 при а ≠ 0. Заметим, что если основание равно нулю, то степень с нулевым показателем не определена (не имеет смысла), т. е. 00 не имеет смысла.
Пример 3
а) 2,70 = 1;
б) ![]()
в) 0° не имеет смысла;
г) (3х)0 = 1 при х ≠ 0;
Д) (x - у)0 = 1 при х ≠ у;
е) (2х + 3у)0 = 1 при 2х + 3у ≠ 0.
После введения нулевой степени формулу ![]() можно применять и в случае, когда m = 0 и n = 0, если а ≠ 0. Формулу
можно применять и в случае, когда m = 0 и n = 0, если а ≠ 0. Формулу ![]() можно применять, когда m и n не только натуральные числа, но и нули, если m ≥ n и а ≠ 0. В старших классах будет показано, что свойства умножения и деления степеней выполняются при любых показателях степеней. Очевидно, что свойства умножения и деления можно применять и совместно.
можно применять, когда m и n не только натуральные числа, но и нули, если m ≥ n и а ≠ 0. В старших классах будет показано, что свойства умножения и деления степеней выполняются при любых показателях степеней. Очевидно, что свойства умножения и деления можно применять и совместно.
Пример 4
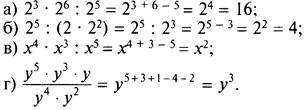
IV. Задания на уроках
№ 403, 405, 408 (в, д), 410 (а, д), 414, 417, 419 (а, в, д), 420 (б, г), 421 (а, б).
V. Контрольные вопросы
— Запишите свойства умножения и деления степеней.
— Сформулируйте словами свойства умножения и деления степеней.
— Чему равна степень с нулевым показателем? Для каких оснований степени?
VI. Творческие задания
1. Определите закономерности и найдите последнюю цифру числа аn для а = 1, 2, 3, ..., 10 и натурального n.
(Ответ: результаты приведены в таблице. Сверху указано основание а, слева — степень n = 1, 2, ..., 8. В последней строке указана повторяемость последней цифры. Видно, что при возведении а = 1, 5, 6, 10 в любую степень последняя цифра не меняется. При возведении а = 2, 3, 7, 8 последняя цифра повторяется при изменении показателя степени на 4. При возведении а = 4, 9 последняя цифра повторяется при изменении показателя степени на 2.)
|
a n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1 |
2 |
3 |
5 |
6 |
7 |
8 |
9 |
0 |
|
|
2 |
1 |
4 |
9 |
6 |
5 |
6 |
9 |
4 |
1 |
0 |
|
3 |
1 |
8 |
7 |
4 |
5 |
6 |
3 |
2 |
9 |
0 |
|
4 |
1 |
6 |
1 |
6 |
5 |
6 |
1 |
6 |
1 |
0 |
|
5 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
6 |
1 |
4 |
9 |
6 |
5 |
6 |
9 |
4 |
1 |
0 |
|
7 |
1 |
8 |
7 |
4 |
5 |
6 |
3 |
2 |
9 |
0 |
|
8 |
1 |
6 |
1 |
6 |
5 |
6 |
1 |
6 |
1 |
0 |
|
4 |
4 |
2 |
4 |
4 |
2 |
2. Используя результаты предыдущей задачи (см. таблицу), найдите последнюю цифру числа:
![]()
(Ответы:
а) 6 (последняя цифра основания 4, показатель степени 2004 кратен 4);
б) 6 (последняя цифра основания 6, число 6 в любой степени оканчивается на 6);
в) 7 (последняя цифра основания 7, показатель 1993 при делении на 4 дает остаток 1, т. е. 1993 = 4 ∙ 498 + 1);
г) 5 (последняя цифра основания 5, число 5 в любой степени оканчивается на 5);
д) 4 (последняя цифра основания 8, показатель степени 1734 при делении на 4 дает остаток 2, т. е. 1734 = 4 ∙ 433 + 2).)
3. Найдите последнюю цифру числа:
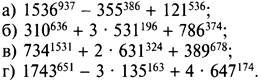
(Ответы:
а) 2 (1536937 оканчивается на 6, 355386 — на 5, 121536 — на 1, и полученное число оканчивается на 6 - 5 + 1 = 2);
б) 9 (310636 оканчивается на 0, 531196 — на 1, 3 ∙ 531196 — на 3, 786374 — на 6, и полученное число оканчивается на 0 + 3 + 6 = 9);
в) 7 (7341531 оканчивается на 4, 631324 — на 1, 2 ∙ 63 1324 — на 2, 389678 — на 1, и полученное число оканчивается на 4 + 2 + 1 = 7);
г) 8 (1743651 оканчивается на 7, 135163 — на 5, 3 ∙ 135163 — на 5, 647174 — на 9, 4 ∙ 647174 — на 6, и полученное число оканчивается на 7 - 5 + 6 = 8).)
4. Определите, является ли число простым или составным:
![]()
(Ответ: все числа составные.)
VII. Подведение итогов уроков
Домашнее задание
№ 404, 406, 408 (г, е), 410 (б, е), 415, 418, 419 (б, г, е), 420 (а, в), 421 (в, г).