Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Использование умножения одночлена на многочлен при преобразовании алгебраических выражений и решении уравнений - ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА - МНОГОЧЛЕНЫ
Цель: рассмотреть практическое применение операции умножения одночлена на многочлен.
Планируемые результаты: использовать умножение одночлена на многочлен для решения прикладных задач.
Тип уроков: уроки общеметодологической направленности.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Выполните умножение:
![]()
2. Упростите выражение ![]() и вычислите его значение при х = -2.
и вычислите его значение при х = -2.
3. Представьте выражение ![]() в виде многочлена и определите его степень.
в виде многочлена и определите его степень.
Вариант 2
1. Выполните умножение:
![]()
2. Упростите выражение ![]() и вычислите его значение при х = -3.
и вычислите его значение при х = -3.
3. Представьте выражение ![]() в виде многочлена и определите его степень.
в виде многочлена и определите его степень.
III. Работа по теме уроков
Навыки умножения одночлена на многочлен используются при преобразовании выражений и решении уравнений.
Пример 1
Упростим выражение ![]() и вычислим его значение при а = 1, b = 2, с = 3.
и вычислим его значение при а = 1, b = 2, с = 3.
Получаем ![]()
![]()
Было учтено переместительное свойство умножения: ba = ab, са = ас и cb = bс. Найдем значение выражения: ![]()
![]()
Пример 2
Докажем, что выражение ![]()
![]() принимает одно и то же значение при любых значениях переменных а и b.
принимает одно и то же значение при любых значениях переменных а и b.
Раскроем скобки и получим ![]()
![]()
Вновь было учтено переместительное свойство умножения: bа2 = а2b.
Пример 3
На простейшем примере обоснуем геометрически правило умножения одночлена на многочлен, т. е. распределительный закон а(b + с) = ab + ас.
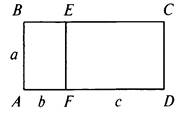
Рассмотрим прямоугольник ABCD со сторонами АВ = а и AD = b + с. Его площадь SABCD = АВ ∙ AD = а(b + с). Этот прямоугольник ABCD состоит из прямоугольников ABEF со сторонами АВ = а и AF = b и площадью SABEF = АВ ∙ AF = а ∙ b и FECD со сторонами EF = а и FD = с и площадью SFECD = EF ∙ FD = а ∙ с. Очевидно, что SABCD = SABEF + SFECD или a(b + с) = ab + ас.
Пример 4
Решим уравнение ![]()
Умножим одночлены на многочлены (т. е. раскроем скобки) и приведем подобные члены. Получаем 2х2 + 6х - 2х2 - 4х = 6 - х или 2х = 6 - х, откуда х = 2.
Пример 5
Решим уравнение ![]()
Умножим все члены уравнения на наименьшее общее кратное чисел 12, 18, 9, т. е. НОК (12, 18, 9) = 36. Получаем
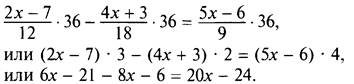
В левой части уравнения приведем подобные члены: -2х - 27 = 20х - 24 или -3 = 22х, откуда х = -3/22.
Пример 6
Решим уравнение ![]()
Умножим все члены уравнения на наименьшее общее кратное чисел 4, 3, 12, т. е. на число 12. Получаем
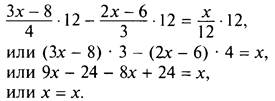
Таким образом, получим тождество х = х. Это означает, что решением данного уравнения является любое число х.
Разумеется, к появлению уравнений и дальнейшему их решению приводят и текстовые задачи.
Пример 7
В первый день завод выпустил на 8 т продукции больше, чем во второй. В третий день завод выпустил в 1,5 раза продукции больше, чем в первые два дня. Всего за эти три дня было выпущено 220 т продукции. Сколько тонн продукции выпускалось каждый день?
По условиям задачи в таблице приведены данные о выпуске продукции в каждый день. В качестве неизвестного х взято количество продукции (в тоннах), выпущенной заводом во второй день. Данные в остальных столбцах таблицы следуют из условий задачи.
|
День |
1 |
2 |
1 + 2 |
3 |
|
Выпуск продукции |
х + 8 |
x |
х + 8 + х |
1,5(х + 8 + х) |
Теперь, исходя из условий задачи, подсчитываем общий выпуск продукции за три дня, используя данные таблицы. Получаем уравнение х + 8 + х + 1,5(х + 8 + х) = 220, или 2х + 8 + 1,5(2х + 8) = 220, или 2х + 8 + 3х + 12 = 200, или 5х + 20 = 220, или 5х = 200, откуда х = 40 (т).
На основе данных таблицы легко подсчитать количество продукции, выпущенной в каждый день.
В первый день: х + 8 = 40 + 8 = 48 (т);
во второй день: х = 40 (т);
в третий день: 1,5(х + 8 + х) = 1,5(2х + 8) = 3х + 12 = 3 ∙ 40 + 12 = 132 (т).
(Ответ: было выпущено: в первый день - 48 т, во второй день - 40 т, в третий день - 132 т.)
IV. Задания на уроках
№ 630 (а, д), 631 (в), 632 (а, в), 633 (б, г), 635 (а), 637 (а, б), 639, 644, 646, 648.
V. Подведение итогов уроков
Домашнее задание
№ 630 (в, е), 631 (г), 632 (б, г), 633 (а, в), 635 (г), 637 (в, г), 640, 645, 647, 649.