Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Системы линейных уравнений с двумя переменными - ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ - СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Цель: рассмотреть понятие системы линейных уравнений с двумя переменными, графический способ решения таких систем.
Планируемые результаты: ознакомиться с системами линейных уравнений с двумя переменными.
Тип уроков: урок проблемного изложения, урок-практикум.
Ход уроков
I. Сообщение темы и цели уроков
II. Работа по теме уроков
Пример 1
В двух седьмых классах 57 учеников. В 7 “А” классе на 5 учеников больше, чем в 7 “Б” классе. Сколько учеников в каждом классе?
Пусть в 7 “А” классе х учеников, в 7 “Б” классе — у учеников. По условию задачи в двух классах 57 учеников, т. е. х + у = 57. В 7 “А” классе на 5 учащихся больше, т. е. х - у = 5. Итак, мы составили два линейных уравнения с двумя переменными (или неизвестными) х + у = 57 и х - у = 5. Чтобы ответить на вопрос задачи, надо найти такие значения переменных х и у, при которых каждое из уравнений будет верным равенством, т. е. нужно найти общее решение этих уравнений. В таких случаях говорят, что надо решить систему уравнений.
Систему уравнений принято записывать с помощью фигурной скобки. Полученную систему уравнений можно записать в виде ![]()
Пара чисел х = 31 и у = 26 удовлетворяет каждому уравнению, так как при их подстановке в уравнения получаем верные числовые равенства: ![]()
Такую пару чисел называют решением системы уравнений.
Решением системы уравнений с двумя переменными называется пара значений переменных, при которых каждое уравнение системы обращается в верное равенство. Решить систему уравнений — значит найти все ее решения или доказать, что решений нет.
В примере 1 было указано решение системы (оно является единственным). Система уравнений может и не иметь решений.
Пример 2
Рассмотрим систему линейных уравнений ![]()
Второе уравнение системы заменим равносильным. Для этого все его члены разделим на число -2 и получим х - 2у = -4. Тогда система уравнений имеет вид ![]()
Из первого уравнения следует, что величина х - 2у равна 5. Из второго уравнения та же величина х - 2у равна -4. Очевидно, что при любых значениях х и у величина х - 2у не может равняться двум различным числам 5 и -4. Поэтому данная система уравнений решений не имеет.
Для решения систем уравнений можно использовать графики этих уравнений (графический способ решения). Достоинство такого способа решения в его наглядности, недостаток — в приближенных значениях решения.
Пример 3
Решим систему уравнении ![]()
Построим графики уравнений системы. Для этого из каждого уравнения выразим переменную у. При этом каждое уравнение системы заменяется равносильным. Получаем систему уравнений 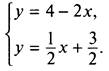
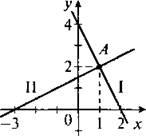
Графиком первого уравнения является прямая I, т. е. координаты всех точек этой прямой удовлетворяют такому уравнению. Графиком второго уравнения является прямая II. Имеем точку А, в которой данные прямые пересекаются (она расположена и на первой, и на второй прямой). Поэтому координаты этой точки удовлетворяют каждому уравнению системы, т. е. являются решением системы уравнений. Определяем координаты точки А и находим х = 1 и у = 2. (Вообще говоря, определить координаты можно лишь приближенно.) Подставив значения х и у в данную систему ![]() убеждаемся, что х = 1 и у = 2 — решение этой системы.
убеждаемся, что х = 1 и у = 2 — решение этой системы.
Итак, в примере 3 система имеет единственное решение. Обсудим вопрос о количестве решений системы двух линейных уравнений с двумя переменными. Общий вид такой системы:
![]()
где x и у — неизвестные, a1, а2, b1, b2, с1, с2 — некоторые числа. Если из каждого уравнения выразить переменную у, то систему (1) можно записать в следующем виде:
![]()
где k1, k2, d1, d2 — некоторые числа. В зависимости от расположения прямых, соответствующих каждому уравнению системы, возможны три варианта при ее решении.
1. Если ![]() (или k1 ≠ k2), то прямые пересекаются и система имеет единственное решение.
(или k1 ≠ k2), то прямые пересекаются и система имеет единственное решение.
Пример 4
Вернемся еще раз к примеру 3. Там рассматривалась система ![]()
В такой системе а1 = 2, b1 = 1, а2 = 1, b2 = -2. Проверим условие ![]() и получим
и получим ![]() После преобразовании система имела вид
После преобразовании система имела вид 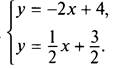
В такой системе k1 = -2 и k2 = 1/2. В ней угловые коэффициенты прямых различны, т. е. k1 ≠ k2. Видно, что для рассматриваемой системы условие единственности решения было выполнено. Соответственно, эта система имеет единственное решение.
2. Если ![]() (или k1 = k2 и d1 ≠ d2), то прямые параллельны и система не имеет решений.
(или k1 = k2 и d1 ≠ d2), то прямые параллельны и система не имеет решений.
Пример 5
Вернемся к примеру 2. Там рассматривалась система ![]()
Для такой системы а1 = 1, а2 = -2, b1 = -2, b2 = 4, с1 = 5, с2 = 8. Проверим условие ![]() и получим
и получим ![]() Из каждого уравнения выразим переменную у и запишем систему в виде
Из каждого уравнения выразим переменную у и запишем систему в виде 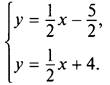
В этой системе ![]() Поэтому условия k1 = k2 и d1 ≠ d2 выполнены. Видно, что для рассматриваемой системы условие отсутствия решений было выполнено, поэтому такая система решений не имеет.
Поэтому условия k1 = k2 и d1 ≠ d2 выполнены. Видно, что для рассматриваемой системы условие отсутствия решений было выполнено, поэтому такая система решений не имеет.
В отсутствии решений легко убедиться, построив графики первого уравнения ![]() (прямая I) и второго уравнения
(прямая I) и второго уравнения ![]() (прямая II). Видно, что прямые I и II параллельны. Соответственно, эти прямые не имеют общих точек, т. е. нет такой точки, координаты которой были бы решением и первого, и второго уравнений. Поэтому данная система решений не имеет.
(прямая II). Видно, что прямые I и II параллельны. Соответственно, эти прямые не имеют общих точек, т. е. нет такой точки, координаты которой были бы решением и первого, и второго уравнений. Поэтому данная система решений не имеет.
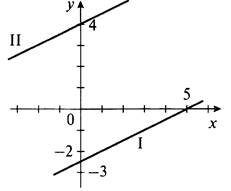
Если система уравнений не имеет решений, то она называется несовместной.
3. Если ![]() (или k1 = k2 и d1 = d2), то прямые совпадают и система имеет бесконечно много решений.
(или k1 = k2 и d1 = d2), то прямые совпадают и система имеет бесконечно много решений.
Пример 6
Рассмотрим систему ![]()
В такой системе а1 = 1, а2 = -2, b1 = -2, b2 = 4, с1 = 5, с2 = -10. Проверим условие ![]() и получим
и получим ![]() Второе уравнение разделим на число -2 и из каждого уравнения выразим переменную у.
Второе уравнение разделим на число -2 и из каждого уравнения выразим переменную у.
Запишем систему в виде 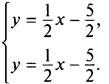
В этой системе ![]()
Очевидно, что равенства k1 = k2 и d1 = d2 выполнены. Условия бесконечного множества решений осуществлены, соответственно, эта система имеет бесконечное множество решений. Если построим графики уравнений х - 2у = 5 и -2х + 4у = -10, то увидим, что они совпадают. Любая точка, расположенная на построенной прямой, имеет координаты, которые являются решением данной системы. Очевидно, что таких решений бесконечно много.
Однако не все пары чисел х и у являются решениями этой системы. Решениями будут такие пары чисел х и у, для которых ![]()
Если система имеет бесконечно много решений, то она называется неопределенной.
Пример 7
При каких значениях а система уравнений ![]() имеет единственное решение?
имеет единственное решение?
Запишем условие единственности решения: ![]()
Используя свойство пропорции, получаем 2(2а - 1) ≠ 3(а + 2) или 4а - 2 ≠ 3а + 6, откуда а ≠ 8. Итак, при всех значениях а, кроме а = 8, данная система имеет единственное решение.
Пример 8
При каком значении а система уравнений ![]() несовместна?
несовместна?
Запишем условие несовместности системы: ![]()
Сначала рассмотрим равенство ![]() Используя свойство пропорции, получаем 5(2а - 1) = 3(2а + 1), или 10а - 5 = 6а + 3, или 4а = 8, откуда а = 2.
Используя свойство пропорции, получаем 5(2а - 1) = 3(2а + 1), или 10а - 5 = 6а + 3, или 4а = 8, откуда а = 2.
Теперь проверим неравенство ![]() При подстановке значения а = 2 получаем
При подстановке значения а = 2 получаем ![]() или
или ![]() (верное неравенство). Итак, при а = 2 данная система несовместна.
(верное неравенство). Итак, при а = 2 данная система несовместна.
Пример 9
При каком значении а система уравнений ![]() неопределенна? Укажите решения системы.
неопределенна? Укажите решения системы.
Запишем условие неопределенности системы: ![]()
Сначала рассмотрим равенство ![]() или
или ![]() Используя свойство пропорции, получаем 2(2а - 1) = а + 1, или 4а - 2 = а + 1, или 3а = 3, откуда а = 1.
Используя свойство пропорции, получаем 2(2а - 1) = а + 1, или 4а - 2 = а + 1, или 3а = 3, откуда а = 1.
Теперь проверим равенство ![]() При подстановке значения а = 1 имеем
При подстановке значения а = 1 имеем ![]() или
или ![]() (верное равенство). Итак, при а = 1 данная система неопределенна.
(верное равенство). Итак, при а = 1 данная система неопределенна.
Подставим значение а = 1 в данную систему и получим ![]()
Поделим второе уравнение на число 2. Получаем систему ![]()
Решением такой системы будет любая пара чисел х и у, в которой х = 8 - 3у, а у — произвольное число.
III. Задания на уроках
№ 1056, 1058 (а), 1059 (б), 1060 (а, б), 1061 (а), 1062 (а, в, д), 1063, 1064 (а).
IV. Контрольные вопросы
— Что называется решением системы уравнений с двумя переменными?
— Что значит решить систему уравнений?
— Сколько решений может иметь система линейных уравнений с двумя переменными?
— Напишите общий вид системы линейных уравнений с двумя переменными.
— Напишите условие единственности решения системы уравнений.
— Напишите условие несовместности системы уравнений.
— Напишите условие неопределенности системы уравнений.
V. Творческие задания
1. При каком значении параметра а система уравнений имеет данное решение (указанное в скобках)?
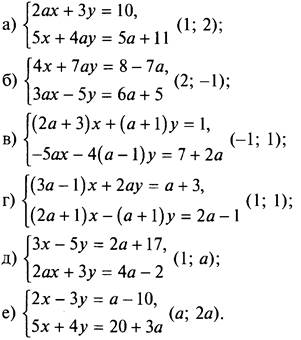
(Ответы: а) а = 2; б) а - любое число; в) а = -3; г) а = 1; д) а = -2; е) а = 2.)
2. При каких значениях параметра а система имеет единственное решение?
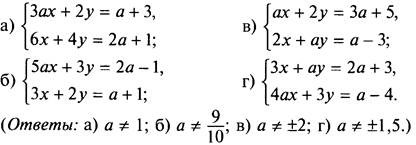
3. При каком значении параметра а система уравнений несовместна?
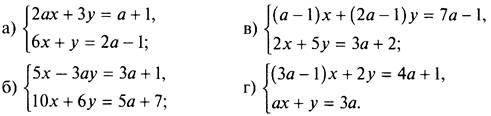
(Ответы: а) а = 9; б) а = -1; в) а = 3; г) а = 1.)
4. При каком значении параметра а система уравнений неопределенна?
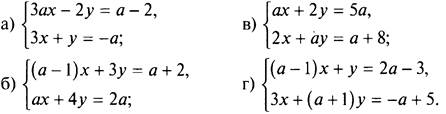
(Ответы: а) а = -2; б) а = 4; в) а = 2; г) а = -2.)
VI. Подведение итогов уроков
Домашнее задание
№ 1057, 1058 (б), 1059 (а), 1060 (в, г), 1061 (б), 1062 (б, г, е), 1064 (б).