Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Допустимые значения переменных в выражениях. Формулы - ВЫРАЖЕНИЯ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ
Цель: сформировать представление о допустимых значениях переменных в алгебраических выражениях и о формулах.
Планируемые результаты: научиться находить допустимые значения переменных в выражениях; иметь представление о простейших формулах.
Тип урока: урок-практикум.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Что называется алгебраическим выражением и переменной?
2. Было закуплено 5 телевизоров стоимостью а руб., 7 приемников стоимостью b руб. и 8 магнитофонов стоимостью с руб. Напишите алгебраическое выражение для вычисления стоимости покупки и найдите его значение при а = 8200, b = 2100 и с = 4300.
3. Найдите значение выражения 2х + 3у - z, если х + у = 3 и у - z = 2.
Вариант 2
1. Как вычислить значение алгебраического выражения при данных значениях переменных?
2. Было закуплено 7 телевизоров стоимостью а руб., 6 приемников стоимостью b руб. и 5 магнитофонов стоимостью с руб. Напишите алгебраическое выражение для вычисления стоимости покупки и найдите его значение при а = 8300, b = 2200 и с = 4100.
3. Найдите значение выражения 3х - 4у - z, если х - у = 5 и у + z = 3.
III. Работа по теме урока
План урока
1. Допустимые значения переменных в выражениях.
2. Простейшие формулы.
3. Деление натуральных чисел.
1. Допустимые значения переменных в выражениях
(Учащиеся с помощью наводящих вопросов сравнивают выражения из примера 1.)
Пример 1
Сравним два алгебраических выражения:
![]()
В первом выражении с переменными а и b выполняются следующие операции: возведение в степень, умножение, сложение, вычитание. Все эти действия можно выполнить с любыми числами (или при любых значениях переменных а и Ь). Поэтому выражение а имеет смысл при любых значениях а и b (или допустимыми значениями для выражения а являются любые значения переменных а и b). В выражении б, помимо упомянутых операций, есть еще одно действие — деление на выражение а - 3. Такая операция выполнима, только если делитель а - 3 не равен нулю (так как делить на нуль нельзя), т. е. а - 3 ≠ 0, откуда а ≠ 3. Поэтому при любых значениях переменной b и значениях а ≠ 3 выражение б имеет смысл, а при а = 3 не имеет смысла. Следовательно, допустимые значения переменных а и b для выражения б — любые значения b и а, кроме а = 3 (т. е. а ≠ 3).
Значения переменных, при которых данное выражение имеет смысл (или выполнимы все действия с этими переменными), называются допустимыми значениями переменных в алгебраическом выражении.
Пример 2
Найдем допустимые значения переменных в алгебраических выражениях:

а) В выражении с переменными х и у выполняются следующие операции: возведение в степень, умножение, вычитание и сложение. Такие действия выполнимы при любых значениях х и у. Поэтому допустимые значения переменных — любые значения X и у.
б) В выражении с переменными х и у выполняются следующие операции: возведение в степень, умножение, вычитание и деление на величину х - 2. Это действие возможно, если делитель х - 2 ≠ 0, т. е. х ≠ 2. Поэтому допустимые значения переменных — любые значения у и любые х ≠ 2.
в) В выражении, помимо других операций, есть и деление на величину х-у. Такое действие возможно, если делитель х - у ≠ 0, т. е. х ≠ у. Поэтому допустимые значения переменных — любые значения х и у, кроме х ≠ у (например, х = 5 и у = 3 — допустимые значения переменных, х = 5 и у = 5 — недопустимые значения).
г) В выражении присутствует деление на величины х + 1 и у - 2. Такие операции возможны, если делители х + 1 ≠ 0 и у - 2 ≠ 0, откуда х ≠ -1 и у ≠ 2. Поэтому допустимые значения переменных — любые значения х ≠ -1 и любые значения у ≠ 2.
2. Простейшие формулы
Равенство, обе части которого являются алгебраическими выражениями, называется формулой.
Пример 3
а) Р = 2 ∙ (а + b) — формула периметра прямоугольника (где Р — периметр, а и b — длины сторон прямоугольника);
б) S = а ∙ b — формула площади прямоугольника (где S — площадь);
в) m = 3 ∙ n — формула числа, кратного 3 (где m — число, кратное 3, n — любое целое число);
г) s = v ∙ t — формула пройденного пути при равномерном движении (где S - пройденный путь, v — скорость движения, t — время движения);
д) v = s/t — формула средней скорости (где v — средняя скорость, s — пройденный путь, t — время, затраченное на этот путь).
3. Деление натуральных чисел
Остановимся на делении натуральных чисел более подробно, так как с этим понятием связано много задач.
Пример 4
а) Число 28 без остатка делится на 7, и в частном получается число 4. Тогда число 28 можно представить так: 28 = 7 ∙ 4, т. е. делимое = делитель ∙ частное.
б) Число 36 без остатка делится на 3, и в частном получается число 12. Тогда число 36 можно представить в том же виде: 36 = 3 ∙ 12, т. е. делимое = делитель ∙ частное.
(Следует обобщить результаты решения этого примера с помощью учащихся.)
Если число m без остатка делится на число р и в частном получается число n, то его можно представить так: m = р ∙ n, т. е. делимое = делитель ∙ частное.
Пример 5
а) Запишем формулу числа, кратного 5: m = 5 ∙ n, так как 5 — делитель, n — некоторое частное (n — целое число).
б) Запишем формулу числа, кратного 13: m = 13 ∙ n, так как 13 — делитель, n — некоторое частное (n — целое число).
Если в эти формулы подставлять различные натуральные числа n, то будем получать числа m, кратные 5 или 13.
Пример 6
Докажем, что сумма и разность двух чисел, кратных 7, также кратны 7.
Первое число m1, кратное 7, запишем в виде m1 = 7 ∙ n1 (где n1 — некоторое частное), второе число m2, кратное 7, запишем в виде m2 = 7 ∙ n2 (где n2 — частное). Найдем сумму чисел m1 и m2и получим m1 + m2 = 7 ∙ n1 + 7 ∙ n2. Это выражение можно записать в виде m1 + m2 = 7 ∙ (n1 + n2). Такая запись означает, что число m1 + m2 делится на 7 и в частном получается число n1 + n2, т. е. сумма чисел m1 и m2 кратна 7.
Аналогично найдем разность чисел m1 и m2 и получим m1 - m2 = 7 ∙ n1 - 7 ∙ n2. Это выражение запишем в виде m1 - m2 = 7 ∙ (n1 - n2). Такая запись означает, что число m1 - m2 делится на 7 и в частном получается число n1 - n2, т. е. разность чисел m1 и m2 кратна 7.
Обсудим теперь деление натуральных чисел с остатком.
Пример 7
а) Число 28 делится на число 9 с остатком. При этом в частном получается 3 и в остатке 1. Тогда число 28 можно представить в виде 28 = 9 ∙ 3 + 1, т. е. делимое = делитель ∙ частное + + остаток (при этом остаток меньше делителя).
б) Число 46 делится на число 8 с остатком. При этом в частном получается 5 и в остатке 6. Тогда число 46 можно записать в виде 46 = 8 ∙ 5 + 6, т. е. делимое = делитель ∙ частное + остаток (при этом остаток меньше делителя).
(Следует обобщить результаты решения этого примера с помощью учащихся.)
Если число m делится на число р и в частном получается число n, а в остатке — число r, то его можно представить в виде m = р ∙ n + r (где r < р), т. е. делимое = делитель ∙ частное + остаток (при этом остаток меньше делителя).
Пример 8
а) Запишем формулу нечетного числа: m = 2 ∙ n + 1 (где n — некоторое частное), так как нечетное число при делении на 2 дает остаток 1.
б) Запишем формулу числа, которое при делении на 7 дает остаток 3: m = 7 ∙ n + 3 (где n — некоторое частное).
Пример 9
При делении на 8 два числа дают остаток 5. Найдите остаток при делении на 8 суммы и разности этих чисел.
Данные числа m1 и m2 можно записать так: m1 = 8 ∙ n1 + 5 и m2 = 8 ∙ n2 + 5 (где n1 и n2 — некоторые частные). Найдем сумму этих чисел: m1 + m2 = 8 ∙ n1 + 8 ∙ n2 + 10. Так как рассматривается деление на 8, то число 10 представим в виде суммы двух чисел, одно из которых кратно 8, т. е. 10 = 8 + 2. Тогда число m1 + m2 запишем в виде m1 + m2 = 8 ∙ n1 + 8 ∙ n2 + 8 + 2 = 8(n1 + n2 + 1) + 2. Эта запись означает, что при делении на 8 числа m1 + m2 в частном получается число n1 + n2 + 1, а в остатке — число 2.
Найдем разность данных чисел: m1 - m2 = 8 ∙ n1 + 5 - 8 ∙ n2 - 5 = 8 ∙ n1 - 8 ∙ n2. Представим разность в виде m1 - m2 = 8 ∙ (n1 - n2). Эта запись означает, что число m1 - m2 кратно 8 (при этом в частном получается n1 - n2), т. е. остаток равен 0.
IV. Задания на уроке
№ 39, 41 (в), 42.
1. Напишите формулу числа, которое при делении на 5 дает остаток:
а) 0;
б) 2;
в) 3.
По этой формуле найдите любое:
а) однозначное число;
б) двузначное число;
в) трехзначное число.
2. Напишите формулу числа, которое при делении на 11 дает остаток:
а) 3;
б) 7;
в) 10.
По этой формуле найдите три любых двузначных числа.
3. Докажите, что сумма и разность двух нечетных чисел является числом четным.
V. Контрольные вопросы
— Какие значения переменных в алгебраическом выражении называются допустимыми?
— Найдите допустимые значения переменных в выражениях:

— Какое равенство называется формулой? Приведите примеры.
— Напишите формулу числа, кратного числу р.
— Напишите формулу числа, которое при делении на число р дает остаток r.
VI. Творческие задания
1. На примере двух чисел, кратных числу n, докажите, что их сумма, разность и произведение также кратны числу n.
Решение
Пусть числа m1 и m2 кратны числу n. Тогда их можно записать в виде m1 = n ∙ a1 и m2 = n ∙ а2 (где а1 и а2 — некоторые частные). Рассмотрим сумму чисел m1 и m2 и получим m1 + m2 = n ∙ а1+ n ∙ а2 = n ∙ (a1 + а2). Эта запись означает, что число m1 + m2 делится на n (при этом в частном получается число a1 + a2), т. е. сумма данных чисел m1 и m2 кратна n.
Найдем разность чисел m1 - m2: n ∙ а1 - n ∙ а2 = n ∙ (а1 - а2). Из этой записи следует, что разность данных чисел кратна n (при этом в частном получается число а1 - а2).
Рассмотрим произведение данных чисел m1 и m2 и получим m1 ∙ m2 = n ∙ а1 ∙ n ∙ a2. Эта запись означает, что число m1 ∙ m2 делится на n (при этом в частном получается число a1 ∙ n ∙ а2), т. е. произведение данных чисел m1 и m2 кратно n. Вообще говоря, из приведенной записи следует, что произведение данных чисел m1 и m2 кратно даже n2.
2. Два числа при делении на число n дают одинаковый остаток. Докажите, что разность данных чисел кратна числу n.
Решение
Даны числа m1 и m2, которые при делении на число n дают одинаковый остаток r. Тогда их можно записать в виде m1 = n ∙ а1 + r и m2 = n ∙ а2 + r (где а1 и а2 — некоторые частные). Найдем разность данных чисел: m1 - m2 = n ∙ а1 + r - (n ∙ а2 + r) = n ∙ а1 + r - n ∙ а2 - r = n ∙ а1 - n ∙ а2 = n ∙ (а1 - а2). Эта запись означает, что число n ∙ (а1 - а2) кратно n (при делении получается частное а1 - а2). Следовательно, разность данных чисел кратна n.
VII. Подведение итогов урока
Домашнее задание
№ 40, 41 (б), 43.
1. Найдите допустимые значения переменных в выражениях:
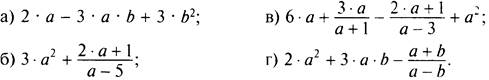
2. Напишите формулу числа, кратного 17. По этой формуле найдите любое:
а) двузначное число;
б) трехзначное число.
3. Напишите формулу числа, которое при делении на 7 дает остаток:
а) 0;
б) 2;
в) 5.
По этой формуле найдите любое:
а) однозначное число;
б) двузначное число;
в) трехзначное число.