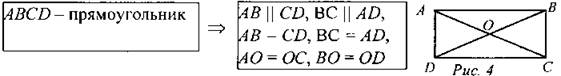ПРЯМОУГОЛЬНИК - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для введения определения прямоугольника, изучения свойств прямоугольника

Термины и понятия

Прямоугольник, диагонали прямоугольника

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики

Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в решении учебных задач.

Регулятивные: проявляют познавательный интерес к изучению предмета.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: умеют контролировать процесс и результат учебной математической деятельности

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Проверка домашнего задания

Цель деятельности

Деятельность учителя

Деятельность учащихся

Выявить трудности, возникшие при выполнении домашнего задания

(И/Ф)

1. Сформулируйте теорему Фалеса.

2. Сформулируйте свойства равнобедренной трапеции.

3. Решите устно задачи по готовым чертежам.

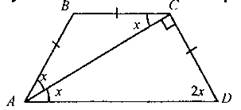
1. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

2. В равнобедренной трапеции углы при основаниях равны, диагонали равны.

3. ∆ABC - равнобедренный.

∠BAC = ∠BCA = х°, как внутренние накрест лежащие при ВС || AD и секущей АС,∠BAD = ∠CDA = 2х°.

Из прямоугольного ∆ACD: ∠CAD + ∠CDA = 90° => х = 30°.

В трапеции ABCD ∠BAC = ∠CAD = 60°, ∠BCD = 120°

II этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятие прямоугольника, доказать свойства и признаки прямоугольника

1. Ввести понятие прямоугольника.

Учащиеся знакомы с прямоугольником еще с начальной школы, поэтому ввести понятие прямоугольника можно в процессе беседы по вопросам:

- Какой четырехугольник называется прямоугольником? (Ученики могут дать различные ответы, например: “Это четырехугольник, у которого все углы прямые”; “Это четырехугольник, у которого противолежащие стороны равны”.)

- Можно ли утверждать, что прямоугольник - это параллелограмм, и почему?

- Чем отличается произвольный параллелограмм от прямоугольника?

- Закончите предложение: “Прямоугольник - это параллелограмм, у которого...”

- Сформулируйте свойства прямоугольника.

(И/Г) 2. Рассмотреть особое свойство диагоналей прямоугольника.

- Исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу.

Параллелограмм

Прямоугольник

Стороны

1.

2.

1.

2.

Углы

1.

2.

1.

2.

3.

Диагонали

1.

1.

2.

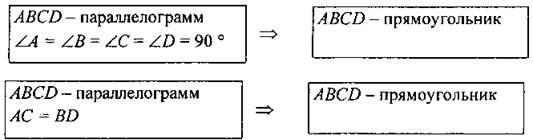
(И/Ф) 3. Рассмотреть признак прямоугольника.

- Как определить, является ли данный параллелограмм прямоугольником? Ответ обоснуйте. (Дать учащимся 3-5 минут на обдумывание и обсудить варианты ответов.)

(Ф) — Выберите верные утверждения (устно):

а) Если в четырехугольнике диагонали равны и делятся точкой пересечения пополам, то этот четырехугольник — прямоугольник.

б) Если в четырехугольнике противоположные стороны параллельны, а все его углы прямые, то этот четырехугольник — прямоугольник.

в) Если в четырехугольнике диагонали равны, то этот четырехугольник - прямоугольник.

г) Если в параллелограмме два угла прямых, то этот параллелограмм - прямоугольник.

д) Если в четырехугольнике два прямых угла и две стороны равны, то этот четырехугольник - прямоугольник.

е) Если в четырехугольнике диагонали равны, а один угол прямой, то этот четырехугольник - прямоугольник

III этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач, опираясь на полученные знания

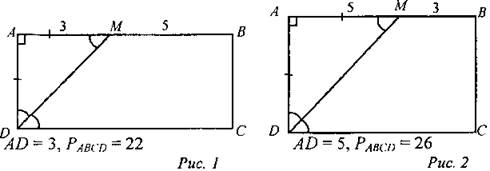
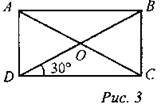
(И/Ф)1. Решите задачу:

В прямоугольнике ABCD биссектриса угла D пересекает сторону АВ в точке М.

Докажите, что ∆ADM - равнобедренный.

Найдите периметр прямоугольника, если сторона АВ оказалась разбита на отрезки длиной 3 см и 5 см. Сколько решений имеет задача?

2. Решите № 403.

Дано: ABCD — прямоугольник, АС ∩ BD = О, ∠CAD = 30°, АС = 12 см.

Найти: Р_AOB

1. Решение:

№ 403.

Решение: ∆ACD - прямоугольный, в нем ∠CAD = 30°, значит,

тогда АВ = CD = 6 см. В прямоугольнике диагонали равны и точкой пересечения делятся пополам, то есть

Р_AOB = АО + ВО + АВ = 6 + 6 + 6 = 18 см.

Ответ: Р_АOB = 18 см

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф)

(И) Домашнее задание: п. 46 прочитать, решить № 401, 404