СВОЙСТВО ВПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА - ОКРУЖНОСТЬ

Цель деятельности учителя

Создать условия для рассмотрения свойства вписанного четырехугольника и показать его применение при решении задач

Термины и понятия

Описанная около четырехугольника окружность, вписанный четырехугольник

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам содержания

Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: формулируют, аргументируют и отстаивают свое мнение.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Проверить домашнее задание

(Ф) К доске вызвать двоих учеников и проверить выполнение домашнего задания.

№ 707.

Решение:

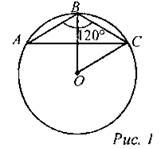
В ∆АВС ∠A = ∠C = (180° - 120°) : 2 = 30°. Тогда ∪BC = 60° => ∠BOC = 60° => ∆ОВС - равносторонний => ОВ = ОС = r = 8 см => диаметр равен 16 см.

Ответ: 16 см.

№ 711.

Решение:

Центр описанной около треугольника окружности совпадает с точкой пересечения его серединных перпендикуляров, а радиус окружности равен расстоянию от центра окружности до любой из вершин треугольника.

В прямоугольном треугольнике центр описанной около него окружности совпадает с серединой гипотенузы, а радиус равен половине гипотенузы

II этап. Решение задач по готовым чертежам

Цель деятельности

Совместная деятельность

Повторить изученный материал и подготовить учащихся к восприятию новой темы

(Ф)

Найти: ∠B.

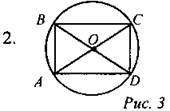
Дано: АВ : ВС = 1 : 2; АС = 5√5.

Доказать: ABCD - прямоугольник.

Найти: АВ, ВС.

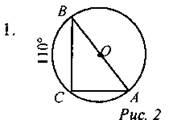
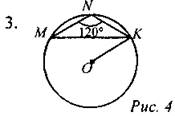
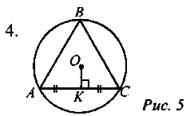
Дано: MN = NK = 4.

Найти: OK.

Дано: ∆АВС - равносторонний. OK = 3

Найти: АВ.

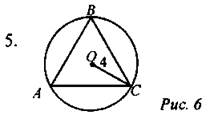
Дано: ∆АВС - равносторонний.

Найти: АВ.

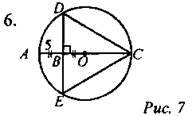
Найти: DC.

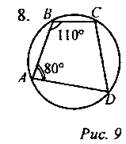
Найти: углы четырехугольника ABCD.

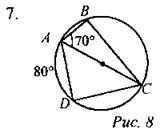
Найти: ∠C, ∠D.

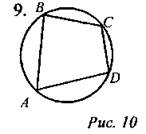
Найти: ∠A + ∠C.

Ответы:

III этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Рассмотреть свойство вписанного четырехугольника

(Ф). 1. Объяснить, что около четырехугольника не всегда можно описать окружность, на примерах ромба, параллелограмма, не являющихся квадратом и прямоугольником соответственно.

2. Для доказательства теоремы о свойстве вписанного четырехугольника учащимся можно предложить самостоятельно решить задачу с последующим обсуждением.

Задача: Докажите, что в любом вписанном четырехугольнике сумма противоположных углов равна 180°.

3. Для доказательства утверждения, обратного свойству вписанного четырехугольника, предложить задание:

Сформулируйте утверждение, обратное свойству вписанного четырехугольника, и выясните его истинность (можно по учебнику).

Теорема. Если сумма противолежащих углов четырехугольника равна 180°, то около него можно описать окружность

IV этап. Закрепление изученного материала

Цель деятельности

Задания для самостоятельной работы

Совершенствовать навыки решения задач

(Ф) 1. Решить № 708 (а), 710.

(И) 2. Выполнить самостоятельную работу.

Вариант I

Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки 5 см и 13 см. Найдите площадь этого треугольника.

Вариант II

Меньший из отрезков, на которые центр описанной окружности равнобедренного треугольника делит его высоту, равен 8 см, а основание треугольника равно 12 см. Найдите площадь этого треугольника

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу на уроке.

- Какой этап урока оказался для вас наиболее сложным?

(И) Домашнее задание: № 708 (б), 709; № 729 (по желанию)