СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНОЙ ДРОБИ И ЦЕЛОГО ВЫРАЖЕНИЯ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цели: формировать умение выполнять сложение и вычитание рациональных дробей и целых выражений; продолжить формирование умения преобразовывать рациональные дроби.

Ход урока

I. Организационный момент.

II. Устная работа.

Вычислите:

III. Объяснение нового материала.

При объяснении целесообразно использовать аналогию с числовыми выражениями.

Выполните сложение:

Известно, что любое целое число может быть представлено в виде дроби со знаменателем 1.

Поэтому Очевидно, что общим знаменателем этих дробей будет b.

Имеем:

Принцип сложения и вычитания рациональной дроби и целого числа вы могли увидеть и при выполнении устной работы. Любой многочлен может быть также представлен в виде рациональной дроби со знаменателем 1. В этом и состоит основная идея сложения и вычитания рациональных дробей и целых выражений.

Пример 1.

Пример 2.

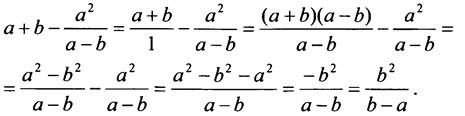
Сделайте вывод о том, как складываются (вычитаются) рациональные дроби с целыми выражениями.

IV. Формирование умений и навыков.

Все задания можно разбить на две группы:

1-я группа. Задания на сложение (вычитание) рациональных дробей с целыми выражениями: № 80, 82, 90 (а, в, д).

2-я группа. Задания на различные более сложные преобразования дробно-рациональных выражений: № 91 (а), 96 (б, г), 97 (а, в), 98 (а), 99 (а).

• Выполнение заданий по учебнику.

№ 91.

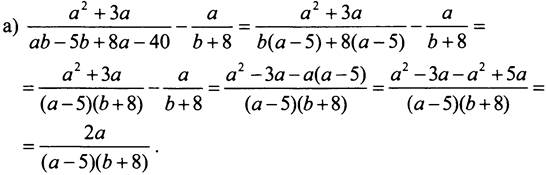
№ 99.

Чтобы доказать тождественное равенство данных выражений, нужно преобразовать их.

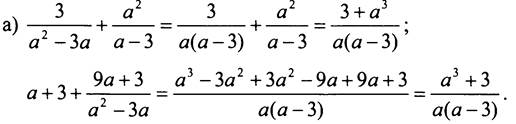
Значит, данные выражения тождественно равны.

• Дополнительное задание. Запишите данные дроби в виде суммы целого выражения и дроби.

Решение

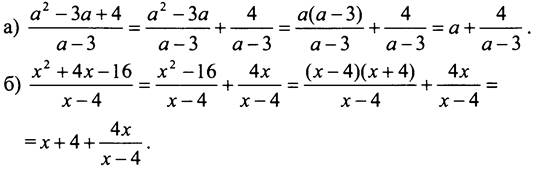
V. Итоги урока.

- Как найти общий знаменатель рациональных дробей?

- Как выполнить сложение или вычитание двух рациональных дробей с разными знаменателями?

- Как выполнить сложение или вычитание рациональной дроби и целого выражения?

Домашнее задание: № 81, 83, 90 (б, г, е), 91 (б), 97 (б, г).