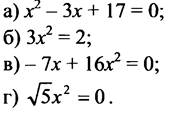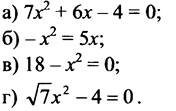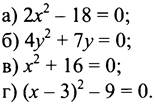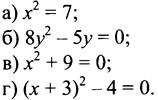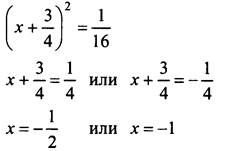ВЫВОД ФОРМУЛЫ КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ - КВАДРАТНЫЕ УРАВНЕНИЯ

Цели: вывести общую формулу нахождения корней квадратного уравнения; формировать умение её использовать.

Ход урока

I. Организационный момент.

II. Проверочная работа.

1. Выпишите коэффициенты а, b, с квадратного уравнения:

Вариант 1	Вариант 2

2. Найдите корни уравнения:

Вариант 1	Вариант 2

3. Решите уравнение приемом выделения квадрата двучлена:

Вариант 1	Вариант 2
2х2 – 24x + 54 = 0	3х2 + 24х - 27 = 0

III. Объяснение нового материала.

Для мотивации изучения общей формулы корней квадратного уравнения достаточно обратить внимание учащихся на два момента:

1) решение квадратных уравнений выделением квадрата двучлена часто приводит к громоздким преобразованиям;

2) каждый раз, решая квадратное уравнение данным приёмом, мы повторяем одни и те же шаги (алгоритм).

Указанные пункты позволяют предположить, что можно провести рассуждения о решении квадратного уравнения приёмом выделения квадрата двучлена для уравнения общего вида.

Для наглядности и осознанности восприятия можно процесс вывода формулы корней квадратного уравнения разбить на несколько шагов, записывая при этом на доске параллельно решение конкретного уравнения и уравнения общего вида.

2х2 + 3х + 1 = 0	ах2 + bх + с = 0, а ≠ 0
Шаг 1. Преобразуем уравнение в приведённое
Шаг 2. Представим второе слагаемое в виде удвоенного произведения, в котором один из множителей есть х
Шаг 3. Прибавим к левой части уравнения выражение и вычтем его:
Шаг 4. Выделим квадрат двучлена:
Шаг 5. Решим полученное уравнение:

Замечаем, что в левой части уравнения находится квадрат выражения (двучлена). Количество корней уравнения зависит от знака правой части уравнения. Более того, 4а² > 0 для любого а ≠ 0, значит для решения важен только знак выражения b² - 4ас. Так появляется понятие дискриминанта D = b² - 4ас (“дискриминант” в переводе с латинского - различитель).

После рассмотрения вопроса о количестве корней квадратного уравнения и вывода их общей формулы желательно вывесить на доску плакат:

Решение квадратного уравнения ах2 + bх + с = 0, а ≠ 0; D = b2 - 4ac. Если D < 0, то уравнение не имеет корней; Если D = 0, то Если D > 0, то

IV. Формирование умений и навыков.

На этом уроке основное внимание следует уделить вопросу определения количества корней квадратного уравнения с помощью дискриминанта. Желательно, чтобы учащиеся за урок выучили формулу D = b² - 4ас и хорошо усвоили алгоритм нахождения корней квадратного уравнения.

1. Выполните упражнение по учебнику: № 533.

2. Докажите, что уравнение не имеет корней:

3. Убедитесь, что уравнение имеет единственный корень, найдите этот корень:

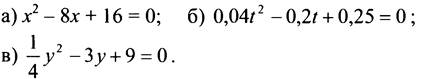
4. Выполните упражнения по учебнику: № 534 (а, в), 535 (а, в, г), 536 (в, д), 538 (а).

V. Итоги урока.

- На чем основан вывод формулы корней квадратного уравнения?

- Как вычислить дискриминант квадратного уравнения?

- Сколько корней может иметь квадратное уравнение?

- Как определить количество корней квадратного уравнения?

- Если квадратное уравнение имеет единственный корень, то что можно сказать о трёхчлене, стоящем в левой части уравнения?

Домашнее задание: № 535 (б, д, е), 536 (б, г, е), 537 (а, в).