Основные понятия (продолжение) - Системы уравнений

Цель: продолжить изучение основных понятий темы.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Определение решения уравнения с двумя переменными.

2. Постройте график уравнения:

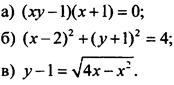
Вариант 2

1. Определение уравнения с двумя переменными.

2. Постройте график уравнения:

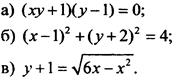
III. Изучение нового материала

4. Системы уравнений с двумя переменными

Уравнения р(х; у) = 0 и q(х; у) = 0 образуют систему уравнений, если возникает задача нахождения пары чисел (х; у), которые удовлетворяют каждому уравнению. При этом такая пара чисел (х; у) является решением системы уравнений. Уравнения, образующие систему, объединяются фигурной скобкой Решить систему уравнений - это значит найти все ее решения или доказать, что решений нет.

Одним из эффективных и наглядных способов решения и исследования уравнений и систем уравнений является графический способ.

Пример 1

Решим систему уравнений

Построим в одной системе координат графики первого х² + y² = 25 (окружность) и второго ху = 12 (гипербола) уравнений.

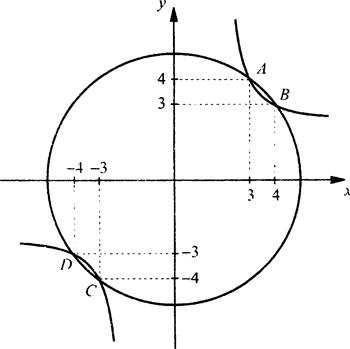
Видно, что графики уравнений пересекаются в четырех точках: А(3; 4), В(4; 3), С(-3; -4) и D(-4; -3), координаты которых являются решениями данной системы. Так как при графическом способе решения могут быть найдены с некоторой точностью, то их необходимо проверить подстановкой. Проверка показывает, что система действительно имеет четыре решения: (3; 4), (4; 3), (-3; -4), (-4; -3).

Пример 2

Решим систему уравнений

Построим в одной системе координат графики первого и второго уравнений. При х = 0 для первого уравнения находим у = √5. При больших значениях |х| имеем: После этого график первого уравнения легко построить.

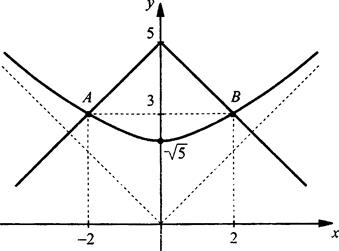
Второе уравнение запишем в виде у = 5 - |x|. Построение его графика также не вызывает груда. Графики пересекаются в двух точках: А(-2; 3) и В(2; 3). Проверкой убеждаемся, что система уравнений имеет два решения: (-2; 3) и (2; 3).

Пример 3

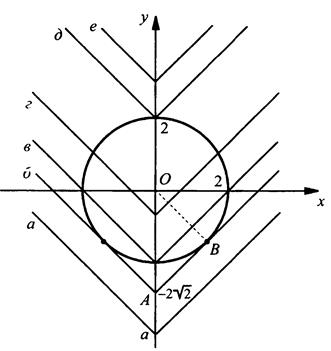
При всех значениях параметра а определим число решений системы уравнений

Построим график первого уравнения х² + у² = 2² (окружность) и второго уравнения у = |х| + а для различных значений параметра а. Этот график пересекает ось ординат в точке у = а. Из прямоугольного равнобедренного треугольника ОАВ найдем гипотенузу ОА = 2√2. Тогда сразу получаем ответ задачи: при система не имеет решений (графики а, е), при - имеет два решения (графики б, г), при a = -2 - три решения (график в) и при a = 2 - одно решение (график д).

Пример 4

При каких значениях параметра а система уравнений имеет единственное решение?

Построим график первого уравнения (верхняя полуокружность, так как y ≥ 0). Также в этой системе координат строим график второго уравнения у = a - х для различных значений параметра а (прямая). Эта прямая пересекает оси координат в точках х = а и у = а.

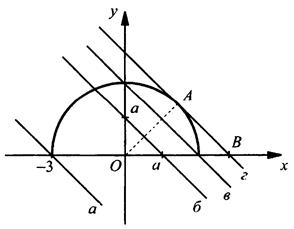
Очевидно, что система уравнений имеет единственное решение, если прямая у = а - х находится между положениями а и в, а также в случае касания г. Для этого случая из прямоугольного равнобедренного треугольника ОАВ найдем гипотенузу OB = 3√2 (соответственно, а = 3√2). Следовательно, при система уравнений имеет единственное решение.

5. Неравенства и системы неравенств с двумя переменными

Часто приходится изображать на координатной плоскости множество решений неравенства с двумя переменными. Напомним, что решением неравенства р(х; y) v 0 с двумя переменными х и у называют пару значений (х; у) этих переменных, которая обращает данное неравенство в верное числовое неравенство.

Пример 5

Рассмотрим неравенство Пара значений переменных (-1; 1) обращает это неравенство в верное числовое неравенство: или 2 ≤ 8 - и является решением неравенства. Пара значений (2; 1) приводит к неверному числовому неравенству: или 11 ≤ 8 - и не является решением данного неравенства.

На примерах рассмотрим, как изображается множество решений неравенства с двумя переменными на координатной плоскости.

Пример 6

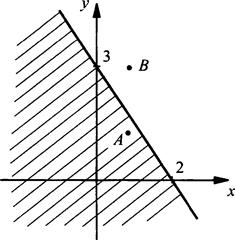
Изобразим на координатной плоскости множество решений неравенства 2у + 3х ≤ 6.

Сначала построим прямую 2у + 3х = 6 или Она разбивает множество всех точек координатной плоскости на точки, расположенные выше ее, и точки, расположенные ниже ее. Возьмем из каждой области по контрольной точке, например A(1; 1) и B(1; 3). Координаты точки А удовлетворяют данному неравенству: 2у + 3х ≤ 6, т. е. 2 ∙ 1 + 3 ∙ 1 ≤ 6. Координаты точки В не удовлетворяют данному неравенству: 2 ∙ 3 + 3 ∙ 1 ≤ 6.

Так как данное неравенство может изменить знак на прямой 2у + 3х = 6, то неравенству удовлетворяет множество точек той области, где расположена точка А. Заштрихуем эту область. Таким образом, изобразили множество решений неравенства 2у + 3х ≤ 6.

Пример 7

Изобразим множество решений неравенства х² + 2х + у² - 4у + 1 > 0 на координатной плоскости.

Построим сначала график уравнения х² + 2х + у² - 4у + 1 = 0. Выделим в этом уравнении уравнение окружности: (x² + 2х + 1) + (у² - 4у + 4) = 4 или (х + 1)² + (y - 2)² = 2². Это уравнение окружности с центром в точке O(-1; 2) и радиуса R = 2. Построим эту окружность. Так как данное неравенство строгое и точки, лежащие на самой окружности, неравенству не удовлетворяют, то строим окружность пунктирной линией.

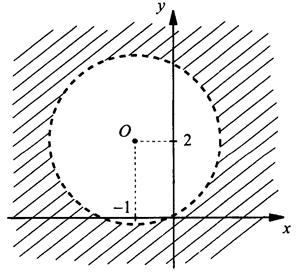
Легко проверить, что координаты центра О окружности данному неравенству не удовлетворяют. Выражение х² + 2х + у² - 4у + 1 меняет свой знак на построенной окружности. Тогда неравенству удовлетворяют точки, расположенные вне окружности. Эти точки заштрихованы.

Пример 8

Изобразим на координатной плоскости множество решений неравенства (у - х²)(y - х - 3) ≤ 0.

Сначала построим график уравнения (у - х²)(у – х - 3) = 0. Им являются парабола y = х² и прямая у = х + 3. Построим эти линии и отметим, что изменение знака выражения (у - х²)(у – х - 3) происходит только на этих линиях. Для точки А(0; 5) определим знак этого выражения: (5 - 0²)(5 - 0 - 3) > 0 (т. е. данное неравенство не выполняется). Теперь легко отметить множество точек, для которых данное неравенство выполнено (эти области заштрихованы).

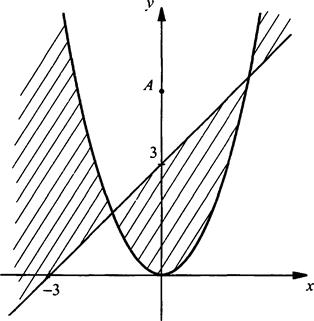
Как видно из рассмотренных примеров, для построения множества решений неравенства с двумя переменными используется метод интервалов на координатной плоскости.

В ряде случаев на координатной плоскости приходится изображать множество решений системы неравенств с двумя переменными. Напомним, что пара значений неизвестных, которая одновременно является решением и первого, и второго неравенств, называется решением системы двух неравенств с двумя переменными.

Пример 9

Рассмотрим систему неравенств с двумя переменными

Пара значений переменных (1; 4) является решением системы неравенств, так как является решением каждого неравенства: или Пара значений переменных (1; 1) не является решением системы неравенств, так как не является решением первого неравенства: или

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений всех неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.

Пример 10

Изобразим на координатной плоскости множество решений системы неравенств

Первое неравенство системы задает на координатной плоскости круг с центром в начале координат и радиуса, равного 1. Второе неравенство задает полуплоскость, расположенную ниже прямой 2х + у = 0. Итак, решениями данной системы неравенств являются точки полукруга (они заштрихованы).

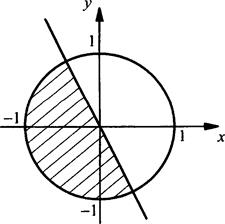
Пример 11

На плоскости хОу изобразим точки, удовлетворяющие системе

Изобразим сначала точки, удовлетворяющие первому неравенству. Сначала построим график границы - график функции у = х² - 2х - 1. Эта парабола пересекает ось Оу в точке у = -1, ось Ох - в точках х₁ = 1 - √2 и х₂ = 1 + √2. Вершина параболы находится в точке (1; -2), ветви параболы направлены вверх. Эта кривая разбила координатную плоскость на две части: часть, заключенную между ветвями параболы, и часть, находящуюся за ветвями параболы. Взяв любую точку (например, (1; -1)) из первой части плоскости, видим, что она удовлетворяет неравенству у ≥ х² - 2х - 1. Поэтому все точки этой части также удовлетворяют неравенству (за исключением границы, так как неравенство строгое).

Аналогично, построив границу (х - 1)² + (y + 2)² = 1, видим, что неравенству (х - 1)² + (у + 2)² ≤ 1 удовлетворяют внутренние и граничные точки окружности.

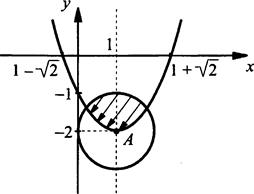
Штриховкой показаны те точки, которые удовлетворяют системе неравенству. Причем стрелки показывают, что данная граница (часть параболы) не входит в множество решений системы неравенств.

Пример 12

Изобразим множество точек, которые являются решениями системы неравенств и вычислим площадь этой фигуры.

Запишем систему неравенств в виде или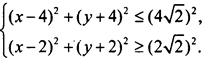

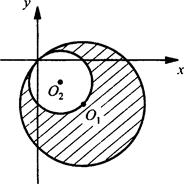
Графиком первого неравенства является круг с центром в точке O₁(4; -4) и радиуса R₁ = 4√2. Графиком второго неравенства являются точки, расположенные за окружностью с центром в точке O₂(2; -2) и радиуса R₂ = 2√2. Итак, решениями данной системы неравенств являются точки, расположенные между двумя касающимися в начале системы координат окружностями (эти точки заштрихованы).

Найдем площадь этой фигуры. Она равна разности площадей окружностей: Таким образом, площадь заштрихованной фигуры равно в 3 раза больше площади малого круга.

IV. Задание на уроках

§ 5, № 18 (а, б); 19 (в, г); 20 (а, в); 21 (а, б); 34 (г); 35 (в); 39 (а).

V. Задание на дом

§ 5, № 18 (в, г); 19 (а, б); 20 (б, г); 21 (в, г); 34 (б); 35 (г); 39 (б).

VI. Творческие задания

1. Найдите значения параметра а, при которых система уравнений имеет ровно два решения:

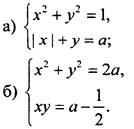
Ответы:

2. Найдите значения параметра а, при которых система уравнений имеет ровно три решения:

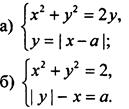
Ответы:

3. Для каждого значения параметра а определите число решений системы уравнений:

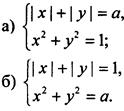
Ответы: а) при нет решений, при а ∈ {1; √2} четыре решения, при а ∈ (1; √2) восемь решений; б) при нет решений, при четыре решения, при восемь решений.

4. Изобразите на координатной плоскости множество решений неравенства:

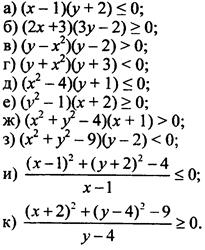
VII. Подведение итогов уроков