Поурочные разработки по Алгебре 9 класс к учебнику А. Г. Мордковича - 2011 год
Контрольная работа по теме Числовые функции - Числовые функции
Цель: проверить знания учащихся с использованием разноуровневых вариантов.
Ход уроков
I. Сообщение темы и цели уроков
II. Варианты контрольной работы
Вариант 1
1. Найдите область определения и область значений функции ![]()
2. Исследуйте на монотонность функцию у = 3х2 + 2х - 7.
3. Найдите наибольшее значение функции у = -3х2 - 6х + 5.
4. Постройте график функции:
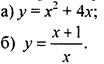
5. Найдите значение выражения ![]()
Вариант 2
1. Найдите область определения и область значений функции ![]()
2. Исследуйте на монотонность функцию у = -5х2 - 4х + 11.
3. Найдите наибольшее значение функции у = -2х2 + 4х - 7.
4. Постройте график функции:
![]()
![]()
5. Найдите значение выражения ![]()
Вариант 3
1. Найдите область определения и область значений функции ![]()
2. Исследуйте на монотонность функцию у = 7х2 - 2|х| + 1.
3. Найдите наибольшее значение функции ![]()
4. Постройте график функции:
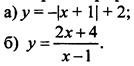
5. Упростите выражение ![]()
Вариант 4
1. Найдите область определения и область значений функции ![]()
2. Исследуйте на монотонность функцию у = -5х2 + 4|х| - 3.
3. Найдите наибольшее значение функции ![]()
4. Постройте график функции:
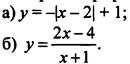
5. Упростите выражение ![]()
Вариант 5
1. Найдите область определения и область значений функции ![]()
2. Исследуйте на монотонность функцию у = (х - 1)|х + 3|.
3. Найдите наибольшее значение функции ![]() При каком значении х оно достигается?
При каком значении х оно достигается?
4. Постройте график функции:
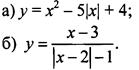
5. Упростите выражение ![]()
Вариант 6
1. Найдите область определения и область значений функции ![]()
2. Исследуйте на монотонность функцию у = |х - 1|(х + 3).
3. Найдите наименьшее значение функции ![]() При каком значении х оно достигается?
При каком значении х оно достигается?
4. Постройте график функции:
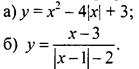
5. Упростите выражение ![]()