Поурочные разработки по Алгебре 9 класс к учебнику А. Г. Мордковича - 2011 год
Комбинаторные задачи - Элементы комбинаторики, статистики и теории вероятностей
Цель: рассмотреть простейшие комбинаторные задачи.
Ход уроков
I. Сообщение темы и цели уроков
II. Изучение нового материала
По мнению авторов, изучение этой темы в средней школе (а тем более в 9 классе) нецелесообразно по следующим причинам:
1) комбинаторика, статистика и теория вероятностей являются изолированными разделами математики, имеют своеобразные логику и методы решения задач;
2) эта тема практически не связана с изучаемым курсом алгебры, не подкреплена повседневной практикой и будет очень быстро забыта;
3) для более или менее осмысленного и логичного изучения таких разделов математики времени явно недостаточно (и взять его неоткуда);
4) даже далеко не в каждом техническом вузе необходимо изучение этих дисциплин;
5) вряд ли средний девятиклассник в состоянии освоить эту тему (надо смотреть правде в глаза). Поэтому разумнее потратить время, отведенное на такие разделы, для более детального изучения основного курса алгебры 9 класса (здесь ситуация весьма далека от идеальной).
В силу перечисленных доводов многие учителя (и не только 9 класса) игнорируют изучение этих разделов математики. Тем не менее такая тема входит в программу 9 класса и ее необходимо рассмотреть.
Комбинаторикой называют область математики, изучающую вопросы о числе различных наборов (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов. Первоначально комбинаторика (и теория вероятностей) возникла в XVI в. в связи с распространением азартных игр (кости, карты и т. д.). В настоящее время комбинаторика используется в теории информации (кодировка и декодировка), линейном программировании (составление расписаний уроков, перевозок) и т. д.
В случае небольшого количества элементов определить число всевозможных комбинаций несложно. Для этого рассматривают все возможные варианты, т. е. используют метод перебора вариантов. Причем необходимо, чтобы такой перебор был логично организован.
Пример 1
Из цифр 3,5,7 составим все возможные трехзначные числа с различными цифрами и определим количество таких чисел.
Поставим, например, на первое место цифру 3. Тогда второй цифрой может быть или 5, или 7, поэтому получаем два трехзначных числа: 357 и 375.
Теперь на первое место поместим цифру 5. Второй цифрой может быть или 3, или 7. Тогда имеем еще два трехзначных числа: 537 и 573.
Наконец на первое место ставим цифру 7. Второй цифрой может быть или 3, или 5. Получаем еще два трехзначных числа: 735 и 753.
Из алгоритма построения чисел понятно, что других трехзначных чисел с цифрами 3, 5, 7 (и без их повторения) не существует. Поэтому получаем шесть трехзначных чисел, удовлетворяющих условию: 357, 375, 537, 573, 735, 753.
Усложним рассмотренную задачу.
Пример 2
Из цифр 3, 5, 7 составим все трехзначные числа, в которых ни одна цифра не повторяется более двух раз. Определим количество таких чисел.
Как и в предыдущей задаче, переберем все возможные варианты. При этом упорядочим такой процесс, построив дерево возможных вариантов. Пусть первая цифра числа 3. Второй цифрой числа может быть цифра 3, или 5, или 7. При этом задача разветвляется на три направления. Получаем двузначные числа 33, 35, 37. Для двузначного числа 33 третьей цифрой может быть или 5, или 7 (цифра 3, очевидно, быть не может). Имеем трехзначные числа 335 и 337.
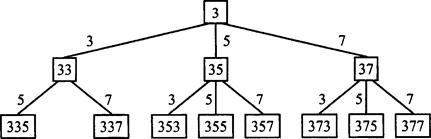
Для двузначных чисел 35 и 37 третьей цифрой будет или 3, или 5 или 7. Получаем два набора трехзначных чисел: 353, 355, 357 или 373, 375, 377. Всего имеем 8 трехзначных чисел с первой цифрой 3.
Если первая цифра 5 или 7, то рассуждения полностью аналогичны приведенным. В каждом из этих случаев также получаем 8 трехзначных чисел. Таким образом, условиям задачи удовлетворяют 8 ∙ 3 = 24 трехзначных числа.
Разумеется, можно рассуждать и другим способом. Пусть по- прежнему первая цифра 3. Тогда трехзначные числа без повторения цифр 357 и 375. Трехзначные числа, в которых повторяется цифра 3, 335, 337, 353, 373. Число, в котором повторяется цифра 5, только одно: 355. Число, в котором повторяется цифра 7, также одно: 377. Таким образом, всего получаем 2 + 4 + 1 + 1= 8 трехзначных чисел с первой цифрой 3. Аналогично можно рассуждать, если первая цифра числа 5 или 7. В каждом из этих случаев также получаем по восемь чисел. Всего условиям задачи удовлетворяют 8 ∙ 3 = 24 трехзначных числа.
Разумеется, перебор вариантов и построение дерева возможных вариантов используются лишь для сравнительно небольшого числа комбинаций. Если таких комбинаций много, то перечислить их затруднительно, но можно подсчитать их количество. Для этого используют правило умножения.
Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Пример 3
Найдем количество различных трехзначных чисел, содержащих цифры 3, 5, 7 и не имеющих одинаковых цифр (см. пример 1).
Очевидно, что первой цифрой может быть одна из трех (3, 5 или 7), например цифра 3 (три исхода). Тогда второй цифрой будет одна из двух оставшихся: 5 или 7 (два исхода). Третьей цифрой будет оставшаяся цифра (один исход). В соответствии с правилом умножения получаем 3 ∙ 2 ∙ 1 = 6 вариантов. Поэтому есть только шесть трехзначных чисел, удовлетворяющих условию задачи (что согласуется с результатами примера 1).
Пример 4
В 9 классе изучают 9 предметов. В среду должны быть проведены 5 различных уроков. Сколькими способами можно составить расписание занятий на среду?
Очевидно, что первым уроком будет один из изучаемых 9 предметов, и мы его выбрали (9 исходов). Тогда вторым уроком может быть поставлен один из 8 оставшихся предметов (8 исходов) и т. д. Поэтому по правилу умножения получаем 9 ∙ 8 ∙ 7 ∙ 6 ∙ 5 = 15 120 вариантов. Таким образом, при условиях задачи расписание при условиях задачи можно составить 15 120 способами.
Пример 5
В четверг в 9 классе пять уроков: алгебра, физика, литература, биология и химия. Сколько вариантов расписания можно составить на четверг?
По аналогии с предыдущим примером первым уроком можно поставить один из 5 предметов (например, физику). Тогда вторым уроком будет один из 4 оставшихся предметов (например, алгебра) и т. д. По правилу умножения имеем 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 120 вариантов составления расписания.
Обсудим детальнее примеры 4 и 5. Видно, что даже несложные задачи комбинаторики приводят к огромному количеству вариантов. Очевидно, что перебрать их невозможно (пример 4). Однако, используя правило умножения, легко посчитать их количество. Как правило, такие расчеты связаны с понятием факториала.
Произведение подряд идущих первых и натуральных чисел обозначают символом п\ и называют “эн факториал”, т. е. ![]() (см. пример 5). При этом 1! = 1. Очевидно, что выполняются равенства:
(см. пример 5). При этом 1! = 1. Очевидно, что выполняются равенства: ![]()
![]() и т. д.
и т. д.
Пример 6
Вычислим: ![]()
Используя понятие факториала и его простейшие свойства, получим:
![]() (непосредственное вычисление);
(непосредственное вычисление);
![]()
![]() (где n ∈ N и n ≥ 2).
(где n ∈ N и n ≥ 2).
Пример 7
Упростим выражение ![]()
Сначала сократим вторую дробь: ![]()
![]() Тогда данное выражение
Тогда данное выражение ![]()
Пример 8
Решим уравнение ![]() (где n ∈ N и n ≥ 2).
(где n ∈ N и n ≥ 2).
Упростим левую часть уравнения, используя определение факториала: ![]() или
или ![]() или
или ![]() или 0 = n2 - 5n + 6. Корни этого квадратного уравнения n = 2 и n = 3 действительно являются натуральными числами и решениями данного уравнения.
или 0 = n2 - 5n + 6. Корни этого квадратного уравнения n = 2 и n = 3 действительно являются натуральными числами и решениями данного уравнения.
Еще раз вернемся к примеру 5, с которым связано понятие перестановок.
Комбинации, каждая из которых содержит n различных элементов, взятых в определенном порядке, называют перестановками из n элементов. Другими словами, имеется n позиций (мест), которые надо заполнить n различными элементами. Число Рn всевозможных перестановок из n элементов вычисляют по формуле Рn = n!.
![]()
В примере 5 мы имеем именно такую ситуацию. Если пронумеровать порядок уроков: 1, 2, 3, 4, 5, то пять изучаемых предметов (алгебра, физика, литература, биология, химия) надо разместить на эти позиции. При каждом варианте получаем некоторую перестановку. Число таких перестановок Р5 = 5! = 120.
Пример 9
Сколько различных пятизначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 1,2, 3, 4?
Из пяти цифр можно составить Р5 перестановок (чисел). Часть из них начинается с нуля. Число таких перестановок Р4. Так как первая цифра в числе не может быть нулем, то количество истинно пятизначных чисел (начинающихся с цифр 1, 2, 3, 4) равно: Р5 - Р4 = 5! - 4! = 4! ∙ (5 - 1) = 4! ∙ 4 = 24 ∙ 4 = 96.
Пример 10
Имеется десять различных книг, четыре из которых - задачники. Сколькими способами можно расставить эти книги на полке так, чтобы все задачники стояли рядом?
Так как задачники должны стоять рядом, то будем рассматривать их как одну книгу. Тогда на полке надо расставить 10 - 4 + 1 = 7 книг. Это можно сделать P7 способами. Для каждой из полученных комбинаций можно сделать Р4 перестановок задачников. Поэтому по правилу умножения число способов расположения книг на полке равно произведению Р7 ∙ Р4 = 7! ∙ 4! = 5040 ∙ 24 = 120 960.
Заметим, что мы затронули самые азы комбинаторики и рассмотрели самые простые комбинации элементов - перестановки. Изучаются также два других вида соединений: размещения и сочетания.
Соединения, отличающиеся друг от друга составом элементов или их порядком, каждое из которых содержит k элементов, взятых из n различных элементов, называют размещениями из n элементов по k (k < n). Другими словами, из n элементов выбирают k элементов и размещают их на k позиций. Число размещений из n элементов по k обозначают символом Ank (читают: А из n по k) и вычисляют по формуле ![]()
Пример 11
Вычислим ![]()
Используя формулу для Ank, найдем:
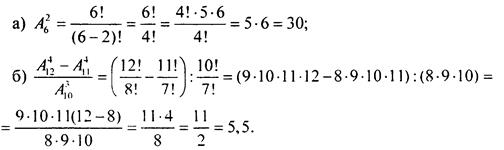
Пример 12
Решим уравнение ![]()
Используем формулы для числа размещений и числа перестановок и получим уравнение: ![]() или
или ![]()
![]() или
или ![]() или
или ![]() или 2 = (n - 2)!. Очевидно, что n - 2 = 2 и n = 4.
или 2 = (n - 2)!. Очевидно, что n - 2 = 2 и n = 4.
Пример 13
Сколько трехзначных чисел с различными цифрами можно составить из цифр 1, 2, 3, 4, 5, 6?
По определению размещений из шести цифр можно составить А63 трехзначных чисел. Это количество равно ![]()
![]() Поэтому можно составить 120 трехзначных чисел.
Поэтому можно составить 120 трехзначных чисел.
Также в комбинаторике рассматривают еще один вид соединений - сочетания. Соединения, отличающиеся друг от друга по крайней мере одним элементом, каждое из которых содержит k элементов, выбранных из n различных элементов, называют сочетаниями из n элементов по k. Порядок следования элементов неважен. Число сочетаний из n элементов по k обозначают символом Сnk (читают: С из n по k) и вычисляют по формуле ![]()
Пример 14
Вычислим ![]()
Используем формулу для числа сочетаний и найдем:
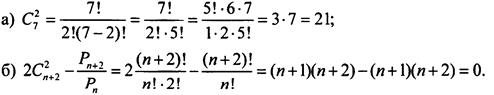
Пример 15
Найдем натуральные значения n, удовлетворяющие условию ![]()
Используем формулу для числа сочетаний и получим уравнение: ![]() или
или ![]() или
или ![]() или 0 = 3n2 - 25n + 8. Корни этого квадратного уравнения n = 1/3 (не натуральное число) и n = 8.
или 0 = 3n2 - 25n + 8. Корни этого квадратного уравнения n = 1/3 (не натуральное число) и n = 8.
Пример 16
У Оли есть 8 разных книг по химии, у Олега 10 книг по физике. Сколькими способами они могут обменяться шестью книгами?
Ольга может выбрать шесть книг из восьми ![]() способами. Независимо от нее Олег может подобрать шесть книг из десяти
способами. Независимо от нее Олег может подобрать шесть книг из десяти ![]() способами. По правилу умножения находим число вариантов обмена:
способами. По правилу умножения находим число вариантов обмена: ![]()
До сих пор рассматривались соединения с различными n элементами. Но некоторые из этих элементов могут быть и одинаковыми. Тогда все приведенные формулы для числа перестановок, числа размещений и числа сочетаний меняются. Для иллюстрации рассмотрим, например, перестановки с одинаковыми элементами.
Перестановки из n элементов, в каждую из которых входят n1 одинаковых элементов первого типа, одинаковых элементов второго типа, n2 одинаковых элементов k-то типа (при этом n1 + n2 + ... + nk = n), называют перестановками из n элементов с повторениями. Число таких перестановок вычисляют по формуле ![]()
Пример 17
Сколькими способами можно расположить в ряд три зеленых, пять красных и восемь желтых лампочек?
Всего имеется n = 3 + 5 + 8 = 16 лампочек. По приведенной формуле их можно расположить ![]()
![]()
III. Контрольные вопросы
1. Соединение из n элементов по k.
2. Перечислите три вида соединений.
3. Определение перестановок из n элементов.
4. Понятие факториала (n!).
5. Число перестановок Рn из n элементов.
6. Определение размещений из n элементов по k.
7. Формула для вычисления числа размещений Аnk.
8. Сочетания из n элементов по k.
9. Число Сnk сочетаний из n элементов по k.
10. Перестановки из n элементов с повторениями.
11. Число Сn(n1, n2, ..., nk) перестановок из n элементов с повторениями.
IV. Задание на уроках
§ 18, № 1; 3; 5; 7; 10; 11 (в, г); 13 (а, б); 14 (в); 15 (а, б); 16; 19; 22; 25 (а, б).
V. Задание на дом
§ 18, № 2; 4; 6; 8; 9; 12 (в, г); 13 (в, г); 14 (г); 15 (в, г); 17; 20; 23; 25 (в, г).
VI. Подведение итогов уроков