Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Сумма бесконечной геометрической прогрессии - Производная - 2-е полугодие
Цель: получить формулу для суммы бесконечной геометрической прогрессии.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Определение возрастающей последовательности.
2. Последовательность (аn) задана формулой ![]() Найдите a1, a5, a10.
Найдите a1, a5, a10.
3. Последовательность (аn) задана формулой аn+1 = 3 - 2аn, где а1 = 2 и n ≥ 1. Найдите первые четыре члена последовательности.
4. Вычислите 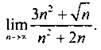
Вариант 2
1. Определение убывающей последовательности.
2. Последовательность (аn) задана формулой ![]() Найдите a1, a5, a10.
Найдите a1, a5, a10.
3. Последовательность (аn) задана формулой an+1 = 3аn - 2, где а1 = 2 и n ≥ 1. Найдите первые четыре члена последовательности.
4. Вычислите 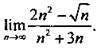
III. Изучение нового материала
Одной из изученных последовательностей является геометрическая прогрессия ![]() которая рассматривалась в 9 классе. Были изучены основные свойства такой прогрессии.
которая рассматривалась в 9 классе. Были изучены основные свойства такой прогрессии.
Если |q| < 1, то прогрессия называется бесконечно убывающей геометрической прогрессией. Для нее, разумеется, как и для любой геометрической прогрессии, справедливы свойства и формулы, приведенные ранее. Кроме того, можно вычислить сумму бесконечного числа членов такой профессии по формуле ![]()
Пример 1
Найдем сумму чисел 6; 3; 3/2; ....
Данные числа образуют бесконечно убывающую геометрическую прогрессию, для которой b1 = 6 и q = 1/2. Тогда ее сумма равна 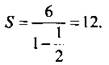
Пример 2
Запишем в виде обыкновенной дроби бесконечную десятичную периодическую дробь 0,(27).
Получим: ![]() - эти дроби образуют бесконечную геометрическую прогрессию, у которой
- эти дроби образуют бесконечную геометрическую прогрессию, у которой 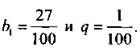 Ее сумма равна
Ее сумма равна 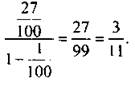
Итак, 0,(27) = 3/11.
Пример 3
Сумма бесконечно убывающей геометрической прогрессии равна 4, а сумма кубов ее членов равна 192. Найдем эту прогрессию.
Пусть дана прогрессия ![]() Тогда ее сумма
Тогда ее сумма ![]() Кубы членов данной прогрессии
Кубы членов данной прогрессии ![]() также образуют геометрическую прогрессию с первым членом b13 и знаменателем q3. Так как при |q| < 1 величина |q3| = |q|3 < 1, то эта прогрессия также бесконечно убывающая и ее сумма
также образуют геометрическую прогрессию с первым членом b13 и знаменателем q3. Так как при |q| < 1 величина |q3| = |q|3 < 1, то эта прогрессия также бесконечно убывающая и ее сумма ![]() Получим систему нелинейных уравнений
Получим систему нелинейных уравнений 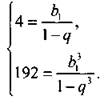 Для решения этой системы возведем первое уравнение в куб:
Для решения этой системы возведем первое уравнение в куб: ![]() и разделим второе уравнение системы на полученное уравнение:
и разделим второе уравнение системы на полученное уравнение: 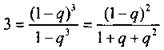 или 2q2 + 5q + 2 = 0. Корни этого уравнения q = -1/2 и q = -2 (не подходит, так как прогрессия бесконечно убывающая и |q| < 1). Теперь из первого уравнения находим
или 2q2 + 5q + 2 = 0. Корни этого уравнения q = -1/2 и q = -2 (не подходит, так как прогрессия бесконечно убывающая и |q| < 1). Теперь из первого уравнения находим ![]()
Пример 4
Сторона квадрата равна а. Середины сторон этого квадрата соединим отрезками. Получился новый квадрат. С этим квадратом поступили так же, как и с данным, и т. д. Найдем суммы сторон, периметров и площадей всех этих квадратов.
Обозначим стороны этих квадратов (начиная с данного): а, а2, а3, ... . Рассмотрим прямоугольный равнобедренный треугольник ABC: ![]() Запишем для него теорему Пифагора:
Запишем для него теорему Пифагора: 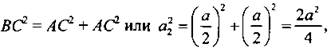 откуда
откуда 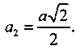 Аналогично из прямоугольного треугольника DEC находим:
Аналогично из прямоугольного треугольника DEC находим: 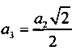 и т. д.
и т. д.
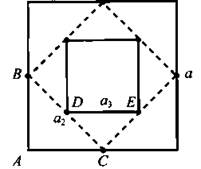
Таким образом, стороны квадратов образуют бесконечно убывающую геометрическую прогрессию ![]() у которой первый член а и знаменатель
у которой первый член а и знаменатель ![]() Найдем ее сумму:
Найдем ее сумму: 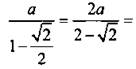
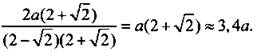
Так как периметр квадрата 4а, то периметры приведенных квадратов также образуют бесконечно убывающую геометрическую прогрессию с первым членом 4а и знаменателем ![]() поэтому ее сумма
поэтому ее сумма ![]()
Площадь квадрата а2 и площади квадратов ![]() образуют бесконечно убывающую геометрическую прогрессию с первым членом а2 и знаменателем 1/2, поэтому сумма площадей
образуют бесконечно убывающую геометрическую прогрессию с первым членом а2 и знаменателем 1/2, поэтому сумма площадей 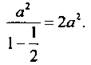
Итак, сумма сторон ![]() периметров -
периметров - ![]() площадей - 2а2.
площадей - 2а2.
IV. Контрольные вопросы
1. Бесконечно убывающая геометрическая прогрессия.
2. Сумма бесконечной геометрической прогрессии.
V. Задание на уроке
§ 25, № 1 (а, б); 4 (в, г);.6 (а); 7 (г); 8 (а, б); 9 (б); 10; 13 (а, б); 14 (а); 15 (в, г).
VI. Задание на дом
§ 25, № 1 (в, г); 4 (а, б); 6 (б); 7 (в); 8 (в, г); 9 (в); 11; 13 (в, г); 14 (б); 15 (а, б).
VII. Подведение итогов урока