Поурочное планирование по алгебре 7 класс
График линейного уравнения с двумя переменными - урок 2 - ІV четверть - Системы линейных уравнений
ЦЕЛЬ УРОКА: Научить учащихся строить график линейного уравнения с двумя переменными, определять, является ли некоторая пара чисел решением этого уравнения.
ПЛАН УРОКА:
№ |
Этап урока |
Содержание |
Время (мин) |
|
1 |
Организационный момент |
Нацелить учащихся на урок |
1 |
|
2 |
Проверка домашнего задания |
Коррекция ошибок |
5 |
|
3 |
Устная работа |
Актуализировать опорные знания |
5 |
|
4 |
Тренировочные упражнения |
Научить строить график линейного уравнения с двумя переменными, определять, является ли некоторая пара чисел решением этого уравнения |
22 |
|
5 |
Самостоятельная работа |
Коррекция ошибок |
8 |
|
6 |
Подведение итогов урока |
Обобщить теоретические сведения, полученные на уроке |
2 |
|
7 |
Сообщение домашнего задания |
Разъяснить содержание домашнего задания |
2 |
|
ХОД УРОКА
I. Организационный момент
II. Проверка домашнего задания (выборочно)
III. Устная работа
1) Найти все пары натуральных чисел, которые являются решениями уравнения х + у = 7.
2) Известно, что точки А (1; ...); В (...; -2); С (0; ...); D (..., 5) принадлежат графику уравнения 2у - 3х = 11.
Найти пропущенные координаты.
3) При каком значении k график линейной функции у = kx + 4 параллелен графику функции:
а) y = 2x + 1;
б) у = -1/7х;
в) у = -3?
Почему?
IV. Тренировочные упражнения.
№ 1050 — на доске и в тетрадях.
Обращаем внимание учащихся на то, что график линейного уравнения с двумя переменными проще строить, если уравнение преобразовано к виду линейной функции у = kx + b.
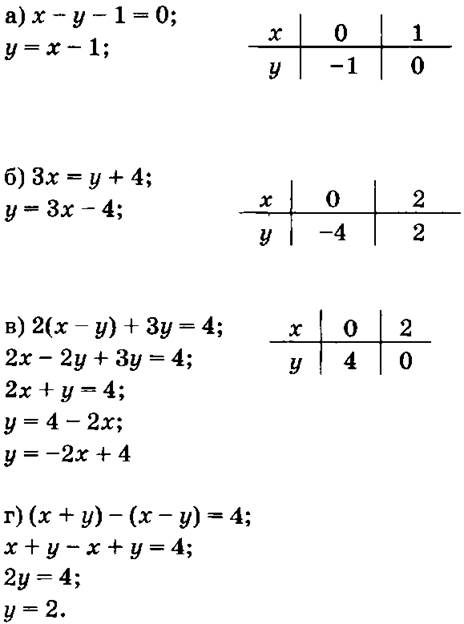
№№ 1051,1052 — на доске и в тетрадях;
№ 1053 — устно;
№ 1055 (а) — самостоятельно, с проверкой,
IV. Самостоятельная работа
Вариант I
Построить графики уравнений: 2х + у - 3 = 0 и у = 1 и указать координаты их точки пересечения.
Вариант II
Построить графики уравнений: х - 4у = 8 и у = -1 и указать координаты их точки пересечения.
V. Итог урока
Контрольные вопросы с. 198 (1-3).
VI. Домашнее задание.
п. 41, №№ 1141 (а), 1151,1148.
На уроках №№ 84—85 напоминаются все термины, связанные с декартовыми прямоугольными координатами на плоскости (абсцисса, ордината, ось абсцисс, ось ординат, начало координат, координатные четверти). Напоминается, что точка М(а; b) есть точка пересечения прямых х = а, у = b. Необходимо обратить особое внимание на то, что решение линейного уравнения с двумя переменными — пара чисел; количество решений такого уравнения бесконечно.
Переход от линейного уравнения с двумя переменными к линейной функции осуществляется с помощью понятия равносильности уравнений. Важно научить учеников уверенному переходу от линейного уравнения с двумя переменными ах + by + с = 0 к линейной функции у = kx + b. Такой переход позволяет график линейного уравнения свести к графику линейной функции, изученной учащимися ранее. Линейное уравнение с двумя переменными устанавливает зависимость между двумя величинами.