Поурочные разработки по Алгебре 8 класс
Урок 2 - ОСНОВНЫЕ ПОНЯТИЯ
Цели: закрепить понятие алгебраической дроби; объяснить составление математической модели для задачи; развивать умение находить значения алгебраических дробей, находить область допустимых значений для дробей; сформировать умение составлять математические модели для задач.
Ход урока
I. Организационный момент.
II. Индивидуальная работа.
Четырем учащимся даются индивидуальные задания на карточках, остальная часть класса проверяет домашнее задание.
Карточка 1
Найдите значение выражения 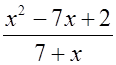 при x = –2.
при x = –2.
Карточка 2
При каких значениях дробь 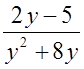 не имеет смысла?
не имеет смысла?
Карточка 3
При каких значениях значение дроби 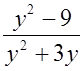 равно нулю?
равно нулю?
Карточка 4
Сравните значения дробей 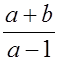 и
и 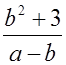 при a = 3, b = 5.
при a = 3, b = 5.
Учащиеся, выполнившие индивидуальные задания, сдают свои работы.
III. Актуализация знаний.
1) Найти значение выражения, заполнить таблицу:
x |
– 3 |
– 1 |
0 |
2 |
8 |
|
2) Придумайте алгебраическую дробь с двумя переменными. Для нее найдите область допустимых значений, значения переменных, при которых значение дроби равно нулю.
3) Разобрать решение заданий 1.6, 1.7, 1.12, 1.20, 1.26.
Для выполнения этих заданий учащимся потребуется широкий круг опорных знаний и умений, сформированных ранее:
– умение выполнять числовые подстановки в буквенные выражения;
– умение решать линейные уравнения;
– использовать для решения некоторых уравнений условие равенства произведения нулю;
– выполнять действия с положительными и отрицательными числами;
– применять формулы сокращенного умножения.
Общей алгоритм рассуждений таков: находят значение переменной, при которых знаменатель дроби обращается в нуль, и затем исключают эти значения из множества всех чисел.
IV. Объяснение нового материала.
Учитель объясняет составление математической модели на примере задачи, разобранной в учебнике на странице 9–10.
Учитель поясняет, что уравнение, составленное по условию задачи, представляет собой математическую модель. Решение задачи состоит из трех этапов:
– составление математической модели;
– работа с составленной моделью;
– ответ на вопрос задачи.
В некоторых задачах используется только первый этап (1.16; 1.17)
№ 1.17.
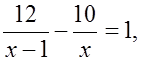 где х – скорость второй группы (км/ч).
где х – скорость второй группы (км/ч).
Вопрос учащимся:
– Почему мы не можем использовать второй и третий этапы?
№ 1.19.
1 э т а п. Составление математической модели.
Пусть х км/ч – скорость автобуса, тогда скорость автомобиля – (х + 30) км/ч.
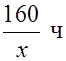 – время, затраченное автобусом.
– время, затраченное автобусом.
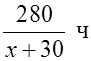 – время, затраченное автомобилем.
– время, затраченное автомобилем.
Так как они затратили одинаковое время, то получим уравнение: 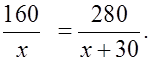
2 э т а п. Работа с составленной моделью.
Используем свойство пропорции:
160 (x + 30) = 280x
160x + 4800 = 280x
12x = 4800
x = 40
3 э т а п. Ответ на вопрос задачи.
Скорость автобуса равна 40 км/ч.
О т в е т: 40 км/ч.
V. Закрепление нового материала.
1) Решить задачи № 1.16; 1.19; 1.21.
В классах с высоким уровнем подготовки можно разобрать одну или несколько сложных задач № 1.33; 1.38.
2) При наличии времени рассмотреть несколько нестандартных заданий:
1. Какое из данных выражений всегда будет целым, если a является натуральным числом:
а) 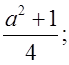 б)
б) 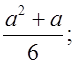 в)
в) 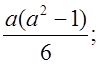
г) 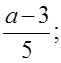 д)
д) 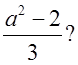
2. Если x, y, z, t – следующие друг за другом натуральные числа, то какое из данных выражений обязательно является четным числом:
а) 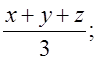 б)
б) 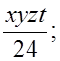 в)
в) 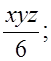
г) 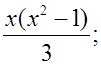 д)
д) 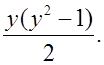
VI. Подведение итогов.
Домашнее задание: изучить теорию из учебника § 1. Решить задачи 1.15; 1.18; 1.27.