Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Целое уравнение и его корни - Уравнения с одной переменной - Уравнения и неравенства с одной переменной
Цель: решение уравнений высоких степеней.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала
Уравнение называют целым, если обе части его являются целыми выражениями (т. е. не содержат деления на выражения с переменными). С помощью равносильных преобразований целое уравнение можно привести к виду Рn(х) = 0, где Рn(х) - многочлен n-й степени.
Пример 1
а) Преобразуем целое уравнение (2х2 + 1)2 – x5 = 1 - 3(х2 - 2). Для этого раскроем скобки, перенесем все члены в одну часть и приведем подобные члены. Получаем: 4х4 + 4х2 + 1 - х5 = 1 - 3х2 + 6, или 0 = -4х4 - 4х2 - 1 + х5 + 1 - 3х2 + 6, или 0 = x5 - 4х4 - 7х2 + 6. Таким образом, имеем уравнение пятой степени 0 = Р5(x), где Р5 (х) = х5 - 4х4 - 7х2 + 6 - многочлен пятой степени.
б) Преобразуем целое уравнение ![]()
Сначала умножим все члены уравнения на наименьший общий знаменатель дробей - число 12 и получим: 3(х2 - 1)2 + 3х2 + 5 = 12(х + 1)2. Затем выполним преобразования, аналогичные использованным в предыдущей задаче. Получаем: 3х4 - 6х2 + 3 + 3х2 + 5 = 12х2 + 24х + 12, или 3х4 - 3х2 + 8 - 12х2 - 24х – 12 = 0, или 3х4 - 15х2 - 24х – 4 = 0. Таким образом, имеем уравнение четвертой степени Р4(х) = 0, где Р4(х) = 3х4 - 15х2 - 24х - 4 - многочлен четвертой степени.
Мы видим, что необходимо научиться решать уравнения n-й степени Pn(х) = 0. При n = 1 такое уравнение является линейным (ах + b = 0, где а ≠ 0 по определению) и имеет единственный корень х = -b/a. При n = 2 получаем квадратное уравнение ax2 + bх + с = 0 (а ≠ 0). Количество корней и сами корни определяются дискриминантом уравнения D = b2 - 4ас. Для D < 0 уравнение корней не имеет, для D = 0 имеет один корень (два одинаковых корня) х = -b/2a, для D > 0 имеет два различных корня ![]() Из рассмотренных линейных и квадратных уравнений (разумеется, со старшим коэффициентом, не равным нулю) видим, что количество корней уравнения не более его степени.
Из рассмотренных линейных и квадратных уравнений (разумеется, со старшим коэффициентом, не равным нулю) видим, что количество корней уравнения не более его степени.
В курсе высшей алгебры доказывается, что уравнение n-й степени Pn(х) = 0 имеет не более n корней. Что касается самих корней, то ситуация намного сложнее. Для уравнений третьей и четвертой степеней известны формулы для нахождения корней. Однако эти формулы очень сложны и громоздки и практического применения не имеют. Для уравнений пятой и более высоких степеней общих формул не существует и существовать не может (как было доказано в XIX в. Н. Абелем и Э. Галуа).
Будем называть уравнения третьей, четвертой и т. д. степеней уравнениями высоких степеней. Некоторые уравнения высоких степеней удается решить с помощью двух основных приемов: разложением многочлена Pn(х) на множители или с использованием замены неизвестной.
Пример 2
Решим уравнение х3 + 2х2 – х - 2 = 0.
Сгруппируем члены многочлена и разложим его на множители. Получаем: (х3 + 2х2) - (х + 2) = 0, или х2(х + 2) - (х + 2) = 0, или (х + 2)(х2 - 1) = 0, или (х + 2)(х - 1)(х + 1) = 0. Произведение множителей равно нулю, если один из них равен нулю. Получаем три линейных уравнения: х + 2 = 0 (корень х = -2), х - 1 = 0 (корень х = 1) и х + 1 = 0 (корень х = -1). Итак, данное кубическое уравнение имеет три корня: x1 = -2, х2 = 1 и х3 = -1.
Пример 3
В этом уравнении мы также будем раскладывать многочлен на множители. Но в данном случае разложение очень неочевидно. Один корень легко угадать (подобрать): x1 = 1. Тогда многочлен должен иметь множитель х - 1. Именно такой множитель мы и будем выделять в многочлене. Получаем: (6х3 - 6х2) – х2 - х + 2 = 0, или 6х2(х - 1) - (х2 - х) - 2х + 2 = 0, или 6x2(x - 1) - x(x - 1) - 2(x - 1) = 0, или (х - 1)(6x2 - х - 2) = 0. Случай х - 1 = 0 мы уже рассмотрели (с него начинали). Теперь решим квадратное уравнение 6х2 - х - 2 = 0 и найдем его корни х2 = 2/3 и х3 = -1/2.
В более сложных случаях используют замену неизвестной. Очень распространены биквадратные уравнения ах4 + bх2 + с = 0 (т. е. уравнения, квадратные относительно х2). Для их решения вводят новую переменную у = х2.
Пример 4
Решим биквадратное уравнение 4х4 - 5х2 + 1 = 0.
Введем новую переменную у = х2 и получим квадратное уравнение 4y2 – 5y + 1 = 0, корни которого y = 1 и у = 1/4. Вернемся к старой переменной х и получим два простейших квадратных уравнения: х2 = 1 (корни x1 = 1 и х2 = -1) и х2 = 1/4 (корни х3 = 1/2 и х4 = -1/2).
Пример 5
Решим уравнение (х2 - 2x)2 - 4(х2 - 2х) + 3 = 0.
Так как и в это уравнение неизвестная jc входит только в виде комбинации x2 - 2х, то удобно ввести замену у = х2 - 2х. Тогда приходим к квадратному уравнению у2 - 4у + 3 = 0, корни которого у1 = 1 и у2 = 3. Возвращаясь к неизвестной х, для у1 получаем: x2 - 2х = 1 (корни ![]() ); для у2: х2 - 2х = 3 (корни х3 = -1, х4 = 3). Так найдены все четыре корня исходного уравнения.
); для у2: х2 - 2х = 3 (корни х3 = -1, х4 = 3). Так найдены все четыре корня исходного уравнения.
Пример 6
Решим уравнение (х2 + 4х + 3)(x2 + 4x + 1) = 48.
Легко сообразить, что уравнение может быть решено так же, как и предыдущее, если ввести замену у = х2 + 4х + 1. Тогда получим уравнение (у + 2)у = 48, или у2 + 2у - 48 = 0, корни которого у1 = -8, у2 = 6. Приходим к совокупности двух уравнений: x2 + 4x + 1 = 6 (корни x1 = -5, x2 = 1) и x2 + 4x + 1 = -8 (корней нет).
Пример 7
Решим уравнение (х - 1)(х + 1)(х + 3)(х + 5) = 105.
При решении этой задачи важно сообразить, что (х - 1)(х + 5) = х2 + 4х - 5, (х + 1)(х + 3) = х2 + 4х + 3. Поэтому, изменив порядок умножения сомножителей в исходном уравнении, получим: [(х – 1)(x + 5)][(х + 1)(x + 3)] = 105, или (х2 + 4х – 5)(x2 + 4х + 3) = 105. Далее эта задача решается аналогично предыдущей. Введем замену у = х2 + 4х – 5 и получим уравнение у(у + 8) = 105, корни которого y1 = -15 и y2 = 7. Решим уравнения х2 + 4х - 5 = -15 (корней не имеет) и х2 + 4х - 5 = 7 (корни х1 = -6 и х2 = 2).
Пример 8
Решим уравнение (х2 + 3х - 8)2 + 2х(х2 + 3х - 8) - 3х2 = 0.
Многочлен, который стоит в левой части уравнения, легко свести к однородному многочлену двух переменных, если ввести замену у = х2 + 3х - 8. Тогда уравнение примет вид: у2 + 2ху - 3х2 = 0. Решив его как квадратное уравнение по переменной у, получим: у = -х ± 2х, т. е. у = -3х и у = х. Возвращаясь к переменной х, имеем два уравнения: х2 + 3х - 8 = -3х (корни ![]() ) и х2 + 3х – 8 = х (корни х3 = -4 и х4 = 2).
) и х2 + 3х – 8 = х (корни х3 = -4 и х4 = 2).
Достаточно часто встречаются целые уравнения, требующие исследования корней.
Пример 9
Докажите, что уравнение (х2 + 2х + 2)(х2 - 4х + 5) = 1 не имеет корней.
Рассмотрим функции y1 = х2 + 2х + 2 = (х + 1)2 + 1 и у2 = х2 - 4х + 5 = (х - 2)2 + 1. Очевидно, что у1 ≥ 1 и у2 ≥ 1. Поэтому произведение у1у2 ≥ 1. Уточним это неравенство. Функция у1 имеет наименьшее значение (равное 1) при х = -1. Но тогда у2(-1) = (-3)2 + 1 = 10 и произведение у1у2 > 1. Аналогично функция у2 имеет наименьшее значение (равное 1) при х = 2. Тогда y1(1) = 22 + 1 = 5 и вновь произведение у1у2 > 1. Поэтому при всех значениях х произведение у1у2 > 1 и данное уравнение корней не имеет.
Пример 10
При каких значениях а корни уравнения х2 - 2ах + (а + 1)(а - 1) = 0 принадлежат промежутку [-2; 1]?
Прежде всего решим это квадратное уравнение: ![]() По условию задачи получаем систему двойных линейных неравенств
По условию задачи получаем систему двойных линейных неравенств 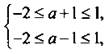 или
или 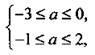 откуда -1 ≤ а ≤ 0.
откуда -1 ≤ а ≤ 0.
В ряде случаев корни уравнения могут иметь достаточно громоздкий вид и для решения задачи приходится использовать графическое представление уравнения.
Пример 11
При каких значениях а один из корней уравнения х2 + 3х + a - 2 = 0 больше 4, а другой меньше 4?
Найдем дискриминант уравнения D = 9 - 4(а - 2) = 17 - 4а и корни ![]() Понятно, что аналитическое решение задачи вызывает трудности, т. к. сводится к решению иррациональных неравенств. Поэтому рассмотрим функцию у = х2 + 3х + а - 2. При всех значениях параметра а ее графиком является парабола, направленная ветвями вверх. Обсудим такие параболы, пересекающие ось абсцисс. При этом точки пересечения являются корнями уравнения х2 - 3х + а - 2 = 0.
Понятно, что аналитическое решение задачи вызывает трудности, т. к. сводится к решению иррациональных неравенств. Поэтому рассмотрим функцию у = х2 + 3х + а - 2. При всех значениях параметра а ее графиком является парабола, направленная ветвями вверх. Обсудим такие параболы, пересекающие ось абсцисс. При этом точки пересечения являются корнями уравнения х2 - 3х + а - 2 = 0.
На рисунке представлены парабола 1, у которой обе точки пересечения х меньше 4; парабола 2, у которой одна из точек меньше 4, а другая больше 4; парабола 3, у которой обе точки больше 4.
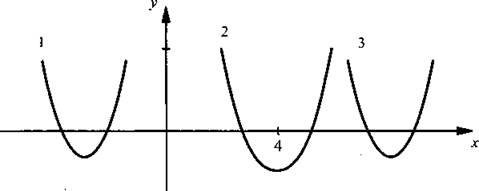
Условию задачи удовлетворяет парабола 2, для которой (в отличие от парабол 1 и 3) у(4) < 0. При таком условии парабола обязательно пересекает ось абсцисс (т. е. данное уравнение обязательно имеет корни).
Найдем у(4) = 42 + 3 · 4 + а – 2 = а + 26 и решим неравенство a + 26 < 0, откуда a < -26. Именно при таких значениях а условия задачи выполнены.
Часто встречаются целые уравнения, содержащие модули.
Пример 12
Решим уравнение х3 - 2х2 + |х| = 0.
Для решения уравнения раскроем знак модуля, рассмотрев два случая.
а) При х ≥ 0 уравнение имеет вид: х3 - 2х + х = 0, или х(х - 1)2 = 0. Корни этого уравнения х = 0 и х = 1 удовлетворяют условию х ≥ 0 и являются решениями данного уравнения.
б) При х < 0 уравнение имеет вид: х3 - 2х2 - х = 0. Так как х ≠ 0, то разделим все члены на х и получим квадратное уравнение х2 - 2х - 1 = 0. Его корни ![]() Условию х < 0 удовлетворяет только корень
Условию х < 0 удовлетворяет только корень ![]() он и является решением данного уравнения.
он и является решением данного уравнения.
Итак, данное уравнение имеет три корня: x1 = 0, х2 = 1 и ![]()
Пример 13
Решим уравнение |3х2 + 5х - 9| = |бх + 15|.
Очевидно, что если модули двух выражений равны, то они либо равны, либо противоположны по знаку. Рассмотрим эти случаи.
а) 3х2 + 5х - 9 = 6х + 15, или 3х2 – х - 24 = 0. Корни этого уравнения x1 = 3 и x2 = -8/3.
б) 3х2 + 5х - 9 = -(6х + 15), или 3х2 + 11х + 6 = 0. Корни этого уравнения х3 = -2/3 и х4 = -3.
Таким образом, данное уравнение имеет четыре корня: x1 = 3, x2 = -8/3, х3 = -2/3, х4 = -3.
В ряде случаев при решении уравнений высоких степеней с параметрами удобно решать уравнение относительно параметра.
Пример 14
Решим уравнение х3 - 2х2 - (m2 - m - 1)х + m2 - m = 0.
Имеем кубическое уравнение с параметром. При этом параметр m входит в уравнение в степени не выше второй. Удобно считать переменную m неизвестной, а переменную х параметром. Получаем уравнение х3 - 2х2 - m2х + mх + х + m2 - m = 0, или (1 - х)m2 + (х - 1)m + х3 - 2х2 + х = 0. Относительно переменной m это уравнение уже является квадратным при m ≠ 1, где а = 1 - х, b = х - 1 и с = х3 - 2х2 + х = х(х - 1)2. Найдем дискриминант D = b2 - 4ас = (х -1)2 - 4(1 - х)х(х - 1)2 = (х - 1)2(1 - 4х + 4x2) = (x - 1)2(2x - 1)2, его корни ![]()
![]() (где x ≠ 1), откуда
(где x ≠ 1), откуда ![]() Решив линейное уравнение m = 1 - х, найдем х = 1 - m. Итак, нашли два корня: х = 1 – m и х = m.
Решив линейное уравнение m = 1 - х, найдем х = 1 - m. Итак, нашли два корня: х = 1 – m и х = m.
Кроме того, для уравнения (1 - х)m2 + (х - 1)m + х3 - 2х2 + х = 0 необходимо проверить значение х = 1. Видим, что х = 1 также является корнем данного уравнения. Итак, данное кубическое уравнение имеет три корня: х1 = 1 - m, х2 = m и х3 = 1.
Большие трудности связаны с уравнениями, одновременно содержащими модули и параметры.
Пример 15
При каких значениях параметра а уравнение |х - 1| + |х + 2| = ах + 1 имеет единственный корень?
Удобно решить задачу графически. Рассмотрим функцию y1 = |х - 1| + |х + 2| и, раскрыв модули, построим ее график. На участке АВ функция имеет вид: у1 = -2х - 1, на участке ВС – у1 = 3 и на участке CD – у1 = 2х + 1. При всех значениях а рассмотрим график функции y2 = ах + 1 (прямые а, б, в).
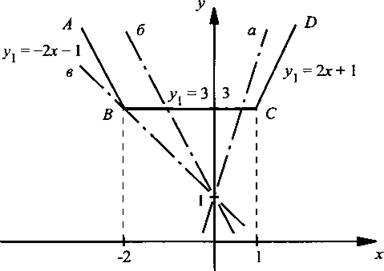
Очевидно, что если график у2 находится ниже участка CD (т. е. 0 ≤ a < 2), то данное уравнение корней не имеет. Если график у2 совпадает с участком CD (т. е. a = 2), то уравнение имеет бесконечное множество решений. Если у2 пересекает участок ВС (прямая а), то уравнение имеет единственный корень (т. е. при а > 2). Очевидно, что если график у2 находится не ниже прямой б (параллельной участку АВ), то уравнение также имеет один корень (т. е. при а ≤ -2). Кроме того, уравнение имеет единственное решение, если прямая у2 проходит через точку В(-2; 3). Получаем уравнение а(-2) + 1 = 3, откуда а = -1.
Итак, при a > 2, a ≤ -2 и а = -1 данное уравнение имеет единственный корень.
III. Контрольные вопросы
1. Определение целого уравнения.
2. Биквадратное уравнение и его решение.
IV. Задание на уроке
№ 265 (а, в, д); 266 (а, б); 268; 270; 272 (а, в, д); 274 (б); 276 (а, в); 278 (а, г); 281 (б); 282 (а); 283 (б); 284 (а).
V. Задание на дом
№ 265 (б, г, е); 266 (в, г); 269; 271; 272 (б, е); 274 (а); 276 (б, г); 278 (б, д); 281 (а); 282 (б); 283 (а); 284 (б).
VI. Творческие задания
1. Линейные уравнения
Решите линейное уравнение.
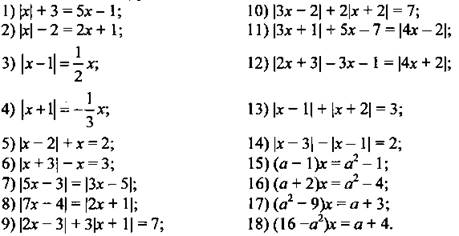
Определите количество корней уравнения.
![]()
При каких значениях а уравнение имеет не менее трех корней?
![]()
Найдите все значения параметра а, при каждом из которых уравнение имеет два различных корня, равноудаленных от точки х = 5.
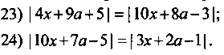
Ответы: ![]()
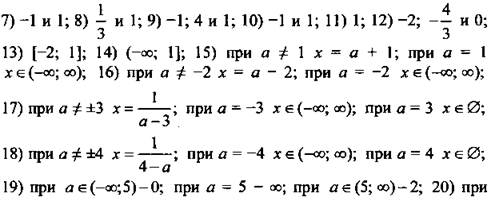
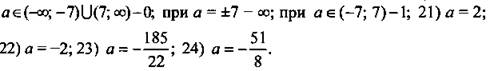
2. Квадратные уравнения
Решите квадратное уравнение.
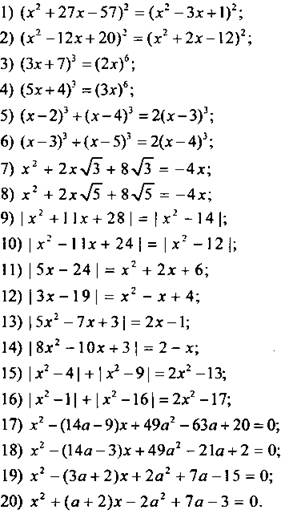
Найдите все значения а, при которых уравнение имеет два корня.
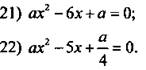
При каких значениях а уравнение имеет корни?
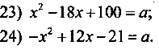
Найдите пары (х; у) целых чисел х и у, для которых выполнено равенство.
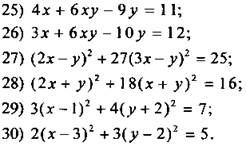
31) Уравнение 3х2 + ax -1 = 0 имеет корни х1 и х2. Найдите:

32) Найдите значения параметра а, при которых корни уравнения (х - 6а)2 + (х - 2а)2 = 128 симметричны относительно точки х = 12.
33) Найдите значения параметра а, при которых больший корень уравнения х2 - (20а - 3)х + 100а2 - 30а = 0 в 6 раз больше, чем его меньший корень.
34) Корни уравнения х2 - (а + 3)х + а + 5 = 0 отличаются в 2 раза. Найдите значение параметра а и корни уравнения х2 - (а + 3)х + а + 5 = 0.
35) При каждом значении параметра а найдите число решений уравнения 9(3х - 1)а2 - (21х - 19)а + 2(х - 1) = 0.
36) Найдите значения параметра а, при которых уравнения х2 + 3х + 7а - 21 = 0 и х2 + 6х + 5а - 6 = 0 имеют хотя бы один общий корень.
37) При каких значениях а корни уравнения х2 - 2ах + (а + 1)(а - 1) = 0 принадлежат промежутку [-5; 5]?
38) При каких значениях а один корень уравнения х2 - (а + 1)х + 2а2 = 0 больше 0,5, а другой меньше 0,5?
39) При каком значении а сумма квадратов корней уравнения х2 + (2 - а)х - а - 3 = 0 минимальная?
Ответы: ![]()
![]()
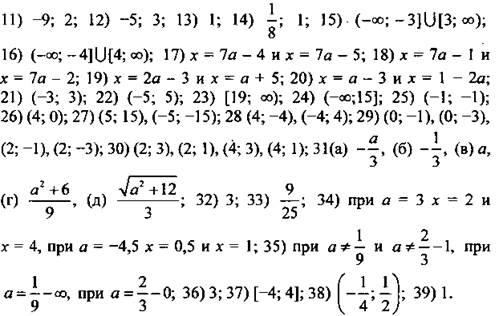
3. Уравнения высоких степеней
Решите уравнение.
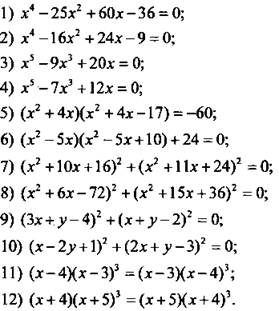
При каком значении а уравнение имеет два корня? Найдите эти корни.
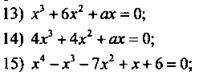
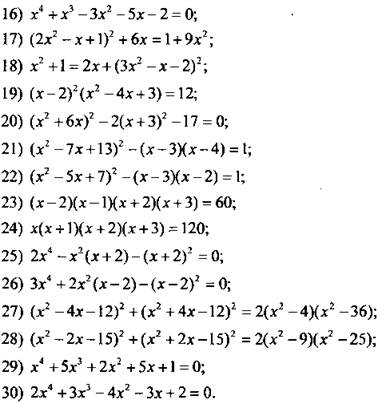
31) Докажите, что уравнение (х2 + 2х + 2)(х2 - 4х + 5) = 1 не имеет корней.
32) Докажите, что уравнение (2х2 - 4х + 3)(х2 - 2х + 2) = 1 имеет единственный корень х = 1.
Ответы: ![]()
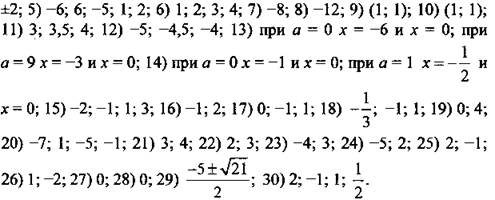
VII. Подведение итогов урока