Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Вычисления. Тождественные преобразования - Повторение курса 7-9 классов
Цель: вспомнить основные вычислительные навыки.
Ход урока
I. Сообщение темы и цели урока
II. Повторение пройденного материала
Выражения, составленные из чисел и переменных с помощью скобок и действий сложения, вычитания и умножения, называют целыми. Также целыми выражениями считают те, в которых используется деление на число, отличное от нуля. Например, следующие выражения являются целыми: ![]()
![]()
Выражения, в которых используется деление на выражение с переменными, называют дробными. Например, выражения ![]()
![]() - дробные.
- дробные.
Целые и дробные выражения называют рациональными.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Целое выражение имеет смысл при любых значениях переменных, дробное выражение - при тех значениях переменных, для которых делители не равны нулю. Например, для выражения ![]() допустимыми являются любые значения а и b. Для выражения
допустимыми являются любые значения а и b. Для выражения ![]() допустимыми являются любые значения х и у, кроме x = -3 и y = 1.
допустимыми являются любые значения х и у, кроме x = -3 и y = 1.
Одночленами называют произведение чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 3а5b2, -2ху2, 5, а, b5 - одночлены.
Степенью одночлена называют сумму показателей степеней всех входящих в него переменных. Например, одночлен 7x5y2z имеет восьмую степень.
Многочленом называют алгебраическую сумму одночленов. Например, х3 - 6х2 + 3х + 1, 5a2b - 2ab + b4 - многочлены.
Одночлен можно рассматривать как многочлен, состоящий из одного члена.
Степенью многочлена называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 6a3b - 5a4b5 + 3a2 - 7b4 равна степени одночлена -5a4b5, т. е. равна 9.
Формулы сокращенного умножения
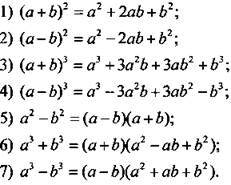
Свойства степени с целым показателем
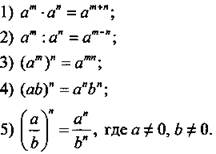
Арифметическим квадратным корнем из неотрицательного числа а называют такое неотрицательное число, квадрат которого равен а.
Свойства арифметического квадратного корня
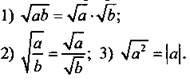
Модулем числа а называют само число а, если оно неотрицательное, и противоположное число, если число а отрицательное, т. е. 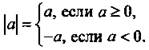
III. Задание на уроке
№ 875 (а, б); 877 (а); 879 (б); 882 (г); 885 (а); 887 (б); 888; 890; 902 (а, д); 905 (а, в); 907 (д); 910 (а, б); 913 (г); 921 (а, б); 922 (а, д).
IV. Задание на дом
№ 875 (в, г); 877 (б); 879 (А); 882 (б); 885 (б); 887 (а); 889; 891; 902 (б, е); 905 (б, г); 907 (е); 910 (в, г); 913 (б); 921 (в, г); 922 (б, г).
V. Подведение итогов урока