Поурочные разработки по геометрии 10 класс
Решение задач по теме «Параллельность прямых и плоскостей» - ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) повторить теорию;
2) подготовить учащихся к контрольной работе.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихс.
1. Проверка домашнего задания.
а) первый ученик у доски решает № 45 (а);
б) второй ученик у доски решает № 46;
в) третий ученик у доски решает № 90.
№ 45 а. Дано: ABCD - параллелограмм; а || ВС; а ∉ (ABCD) (рис. 1).
Доказать: а и CD - скрещивающиеся.
Найти: угол между а и CD, если ∠BCD = 50°.
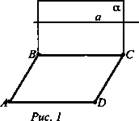
Решение:
I. 1) Так как а || ВС, то проведем через них плоскость α.
2) D ∉ α, так как иначе DC ∈ α, то есть α совпала бы с плоскостью ABCD и а ∈ (ABCD), что противоречит условию.
3) Тогда DC ∩ α в точке С ∉ а;
4) Вывод: по теореме а и CD - скрещивающиеся.
II. Проведем через точку С прямую, параллельную прямой а. Это будет прямая СВ. Значит, угол между а к СВ равен углу между прямыми СВ и CD, то есть ∠BCD = 50°. (Ответ: 50°.)
№ 47. Дано: ABCD - пространственный четырехугольник; АВ = CD, N - середина AD; М - середина ВС (рис. 2).
Доказать: угол между АВ и MN и угол между CD и MN равны.
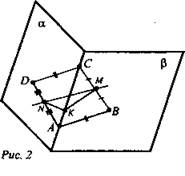
Решение:
1. Точка К - середина АС. Через точку М проведем МК || АВ, МК - средняя линия ΔABC, ∠(MN, АВ) = ∠KMN.
2. МК - средняя линия ΔABC, МК || АВ; МК = 1/2АВ. Через точку N проведем NK || DC, NK - средняя линия ΔADC, ∠(DC, MN) = ∠MNK.
3. NK - средняя линия ΔCDP; NK || CD; NK = 1/2CD.
4. КМ = 1/2АВ, NK = 1/2DC, так как АВ = DC, то КМ = NK, то есть ΔNMK - равнобедренный.
5. Вывод: ∠KMN = ∠MNK, что и требовалось доказать.
6. ![]()
№ 90 (рис. 3).
а) Решение: Если АВ ∈ α и АВ || DC, то DC || α;
б) Решение: АВ не параллельно CD. Так как АВ и CD лежат в одной плоскости ABCD, то АВ ∩ CD. Значит, CD пересекает плоскость α.
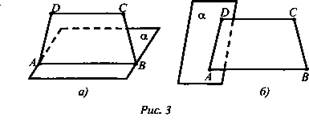
2. Работа по карточкам (см. приложение)
Три ученика работают по карточкам.
Остальные учащиеся решают задачу по планиметрии.
Дано: ABCD - трапеция, описанная около окружности. АВ = CD. Т, М, Р, Е - точки касания окружности. ВТ = 2, АЕ = 8 (рис. 4).
Найти: SABCD.
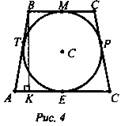
Решение:
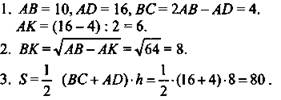 (Ответ: 80.)
(Ответ: 80.)
Решение задач к карточка.
Карточка № 1
№ 1. Решение:
а) Так как К - середина АВ, и М - середина ВС, то КМ - средняя линия ΔАВС. КМ || АС и КМ = 1/2АС. Так как ACFE - квадрат, то EF || АС.
Вывод: KM || EF.
б) Так как ACFE - квадрат, то ![]()
(Ответ: а) КМ || EF; б) КМ = 4 см.)
№ 2. Дано: ABCD - трапеция: BC || AD - основания. AD ∈ α; точка Е - середина АВ; точка F середина CD; EF ∉ α (рис. 5).
Доказать: EF || α.
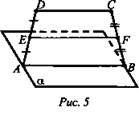
Доказательство:
1. Так как Е - середина АВ, F - середина CD, то EF - средняя линия трапеции ABCD. EF || AD - по свойству средней линии.
2. AD ∈ α - по условию.
3. Вывод: EF || α (по признаку параллельности прямой и плоскости, п. 6, стр. 12).
№ 3. Дано: точки А, В, С, и D не лежат в одной плоскости (рис. 6).
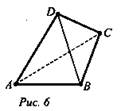
Найти: а) прямую, скрещивающуюся с АВ; б) прямую, скрещивающуюся с ВС.
(Ответ: a) DC; б) AD.)
Карточка № 2
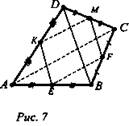
№ 1. Дано: А, В, С, D - не лежат в одной плоскости; точка Е - середина АВ; точка F - середина ВС; точка М - середина DC; точка К - середина AD (рис. 7).
а) Доказать: EFMK - параллелограмм.
б) Найти: P(EFMK), если АС = 6 см; BD = 8 см.
Решение:
а) КМ - средняя линия ΔADC ⇒ КМ || АС; КМ = 1/2АС; MF - средняя линия ΔDCB ⇒ MF || BD; MF = 1/2BD; EF - средняя линия ΔABC ⇒ EF || AC; EF = 1/2AC; KE - средняя линия ΔABD ⇒ KE || BD; KE = 1/2BD. Значит, ![]()
Вывод: EFMK - параллелограмм.
б) ![]() или
или ![]()
![]() (Ответ: a) EFMK - параллелограмм; б) P(EFMK) = 14 см.)
(Ответ: a) EFMK - параллелограмм; б) P(EFMK) = 14 см.)
№ 2. Дано: α - плоскость; точка ![]()
![]() (рис. 8).
(рис. 8).
Доказать: b ∈ α.
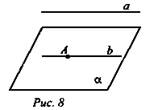
Доказательство: Пусть b ∉ α, но b проходит через точку A ∈ α, ⇒ b ∩ α в точке А. А так как a || α, то получается, что b ∩ α, что противоречит условию. Значит, прямая b ∈ α, что и требовалось доказать. (Ответ: b ∈ α.)
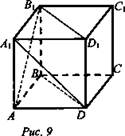
№ 3. Дано: ABCDA1B1C1D1 - куб (рис. 9).
Укажите: три прямые, проходящие: а) через точку D и скрещивающиеся с прямой АВ1; б) через точку B1 и скрещивающиеся с прямой A1D1.
Решение:
а) прямая АВ1 ∈ (AA1B1B); прямые DD1, DC и DB - скрещивающиеся с прямой АВ1, так как они не лежат в плоскости (АА1В1В);
б) прямая A1D ∈ (AA1D1D); прямые B1D1, В1С1 и ВВ1 - скрещивающиеся с прямой A1D, так как они не лежат в плоскости (AA1D1D). (Ответ: a) DD1, DC, DB; б) B1D1; В1С1; ВВ1.)
Карточка № 3
№ 1. Дано: (ABC) - плоскость; точка M ∉ (ABC); точка D - точка пересечения медиан ΔМАВ; точка Е - точка пересечения медиан ΔМВС (рис. 10).
а) Доказать: ADEC - трапеция.
б) Найти: DE, если АС = 12 см.
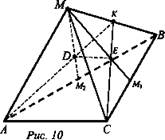
Решение:
а) Рассмотрим ΔАКС и ΔDEK. У ни.
а) ![]() (по свойству медиан в треугольниках); б) ∠K - общий. Значит, ΔАКС и ΔDEK подобны по двум сторонам и углу между ними.
(по свойству медиан в треугольниках); б) ∠K - общий. Значит, ΔАКС и ΔDEK подобны по двум сторонам и углу между ними.
Из этого следует, ![]() и они являются соответственными при прямых DE и АС и секущих АК и СК.
и они являются соответственными при прямых DE и АС и секущих АК и СК.
Вывод: DE || АС, значит, ADEC - трапеция.
б) Так как ΔАKC ~ ΔDKE с коэффициентом подобия k = 1/3, то ![]() (Ответ: a) ADEC - трапеция; б) DE = 4 см.)
(Ответ: a) ADEC - трапеция; б) DE = 4 см.)
№ 2. Дано: АА1, ВВ1, СС1 - отрезки, не лежащие в одной плоскости. АА1 ∩ ВВ1 ∩ СС1 в точке О. Точка О - их середина (рис. 11).
Доказать: прямая АВ || (А1СВ1).
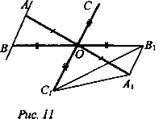
Доказательство: Рассмотрим плоскость, проходящую через отрезки АА1 и ВВ1 (такая есть и единственная, так как АА1 ∩ ВВ1 в точке О).
В этой плоскости лежит четырехугольник АВА1В1, диагонали которого точкой пересечения О делятся пополам. Значит, АВА1В1 - параллелограмм. Следовательно, АВ || А1В1, а А1В1 прямая, которая лежит в плоскости А1СВ1, следовательно, АВ || (А1СВ1). (Ответ: АВ || (А1СВ1).)
Выслушивается и проверяется решение домашних задач.
III. Решение задач (фронтальная работа.
Дополнительные задачи, № 88 стр. 32.
Дано: AC || BD - прямые; АС ∩ α в точке А; DB ∩ α в точке В; точки С и D лежат по одну сторону от α; АС = 8 см, BD = 6 см, АВ = 4 см (рис. 12).
Доказать: CD ∩ α в точке Е.
Найти: BE.
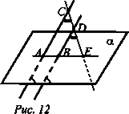
Решение:
1. Проведем плоскость через прямые АС и BD. Если CD || АВ, то ABCD - параллелограмм, значит АС = BD, но АС = 8 см, BD = 6 см. Значит CD не параллельна АВ, но так как они лежат в одной плоскости, то CD ∩ АВ в точке Е, то есть CD ∩ α в точке Е.
2. а) ![]() как соответственные при AC || BD и секущих АЕ и СЕ.
как соответственные при AC || BD и секущих АЕ и СЕ.
б) ΔEDB ~ ΔЕСА (по трем углам) ⇒ ![]()
![]() (Ответ: 12 см.)
(Ответ: 12 см.)
Дополнительные задачи, № 97 стр. 32 (рис. 13 а, б, в).
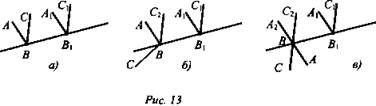
Решение: Рассмотрим ∠АВС и ∠А1В1С1, у которых АВ || А1В1 и ВС || В1С1. Проведем прямую ВВ1.
а) ![]() тогда ∠АВС = ∠А1В1С1 (см. п. 8) (рис. 13 а).
тогда ∠АВС = ∠А1В1С1 (см. п. 8) (рис. 13 а).
б) ![]() тогда рассмотрим ∠АВC2 - смежный к ∠АВС ⇒ (по теореме пункта 7) ∠АВС2 = ∠ А1В1С1, значит,
тогда рассмотрим ∠АВC2 - смежный к ∠АВС ⇒ (по теореме пункта 7) ∠АВС2 = ∠ А1В1С1, значит, ![]()
![]() (рис. 13 б).
(рис. 13 б).
в) ![]() тогда рассмотрим ∠А2ВС2 - вертикальный к ∠АВС. Следовательно,
тогда рассмотрим ∠А2ВС2 - вертикальный к ∠АВС. Следовательно, ![]()
![]() (см. рис. 13 в).
(см. рис. 13 в).
№ 87 б. Дано: ABCDA1B1C1D1 - параллелепипед. ![]() (рис. 14).
(рис. 14).
Построить: MNK - сечение.
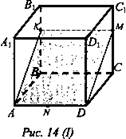
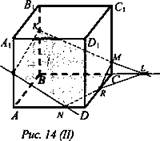
Построение: Возможны два случая:
I. 1) Соединим точки К и М, КМ || ВС;
2) ![]() (точка N ∈ AD);
(точка N ∈ AD);
3) Соединим К с А и M c D;
4) AKMD - искомое сечение.
II. 1) КМ ∩ ВС в точке L;
2) Через точку N проведем прямую а || КМ;
3) а ∩ АА1 в точке Р;
4) Соединим точу К и точку Р;
5) NL ∩ DC в точке К;
6) KPNRM- искомое сечение.
IV. Подведение итогов
Домашнее задание
П. 1-9. № 87 а, 46, 93.
Вопросы № 9-16 (стр. 31-32).