Поурочные разработки по геометрии 10 класс
Решение задач на перпендикулярность прямой и плоскости - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
2) выработать навыки решения основных типов задач на перпендикулярность прямой и плоскости.
Ход урока
I. Организационный момент
Сообщить тему и план урока.
II. Актуализация знаний учащихся
1) Теоретический опрос.
Сформулировать и доказать теорему о прямой, перпендикулярной к плоскости (подготовиться у доски одному из учащихся, затем заслушать его ответ всем классом).
2) Индивидуальные письменные задания:
- доказать теорему о перпендикулярности двух параллельных прямых к третьей (1 ученик);
- доказать теорему, устанавливающую связь между параллельностью прямых и их перпендикулярностью к плоскости (1 ученик);
- доказать теорему, обратную к теореме, устанавливающей связь между параллельностью прямых и их перпендикулярностью к плоскости (1 ученик);
- доказать признак перпендикулярности прямой и плоскости (1 ученик).
3) Самостоятельное решение задач по готовым чертежам с последующей проверкой и обсуждением по необходимости.
I уровень: № 1, 2, 5.
II уровень: № 3, 4, 6.
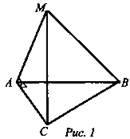
Точка М лежит вне плоскости ABC.
1. Рис. 1. Доказать: прямая АС перпендикулярна плоскости АМВ.
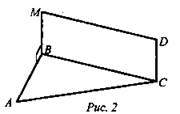
2. Рис. 2. BMDC - прямоугольник. Доказать: прямая CD перпендикулярна плоскости ABC.
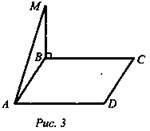
3. Рис. 3. ABCD - прямоугольник. Доказать: AD ⊥ АМ.
Решение к задачам 1-6.
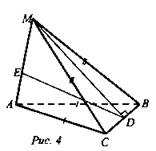
4. Рис. 4. Доказать: ВС ⊥ DE.
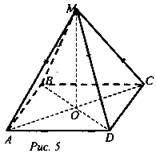
5. Рис. 5. ABCD - параллелограмм. Доказать: прямая МО перпендикулярна плоскости ABC.
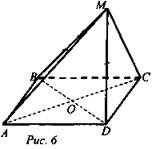
6. Рис. 6. ABCD - ромб. Доказать: прямая BD перпендикулярна плоскости АМС.
№ 1
Доказательство:
AC ⊥ АВ (по условию), AC ⊥ AM (по условию).
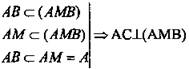 (по признаку перпендикулярности прямой и плоскости).
(по признаку перпендикулярности прямой и плоскости).
№ 2
Доказательство:
Так как BMDC - прямоугольник, то ∠MBC = 90°, значит,
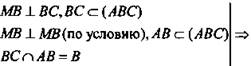 MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости).
MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости).
MB || DC (по свойству сторон прямоугольника). Следовательно, DC ⊥ (ABC) (по теореме о связи между параллельностью прямых и их перпендикулярностью к плоскости).
№ 3
Доказательство:
1) Так как ABCD - прямоугольник, то ∠ABC = 90°, значит, ВС ⊥ АВ, АВ ⊂ (АВМ)
![]() ВС ⊥ (АМВ) (по признаку перпендикулярности прямой и плоскости).
ВС ⊥ (АМВ) (по признаку перпендикулярности прямой и плоскости).
2) BC || AD (по свойству сторон прямоугольника). Следовательно, AD ⊥ (AMB) (по теореме о связи между параллельностью прямых и их перпендикулярностью к плоскости).
3) ![]() AD ⊥ AM (по определению прямой, перпендикулярной плоскости).
AD ⊥ AM (по определению прямой, перпендикулярной плоскости).
№ 4 (рис. 7)
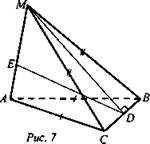
Доказательство: Так как ΔСМВ - равнобедренный (по условию) и MD - высота, то MD - медиана (по свойству высоты равнобедренного треугольника).
Значит, CD = BD (по определению медианы).
1) Так как ΔAВС - равнобедренный (по условию) и AD - медиана (по определению), то AD высота (по свойству медианы равнобедренного треугольника). Значит, ВС ⊥ AD.
2) 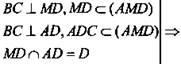 ВС ⊥ (AMD) (по признаку перпендикулярности прямой и плоскости).
ВС ⊥ (AMD) (по признаку перпендикулярности прямой и плоскости).
3) ![]() ВС ⊥ DE (по определению прямой, перпендикулярной плоскости).
ВС ⊥ DE (по определению прямой, перпендикулярной плоскости).
№ 5
Доказательство:
1) AC ∩ BD = О; АО = ОС, ВО = OD (по свойству диагоналей параллелограмма).
2) ΔBMD - равнобедренный (по условию) и МО - медиана (по определению), значит, МО - высота (по свойству медианы равнобедренного треугольника).
Следовательно, МО ⊥ BD.
3) В ΔАМС: МО ⊥ АС (доказывается аналогично п. 2).
4) 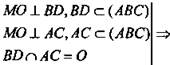 МО ⊥ (AВС) (по признаку перпендикулярности прямой и плоскости).
МО ⊥ (AВС) (по признаку перпендикулярности прямой и плоскости).
№ 6 (рис. 8)
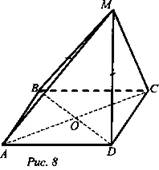
Доказательство: AC ⊥ BD и АО = ОС, ВО = OD (по свойству диагоналей ромба). ΔBMD - равнобедренный (по условию) и МО - медиана (по определению), значит, МО высота (по свойству медианы равнобедренного треугольника).
Следовательно, МО ⊥ BD.
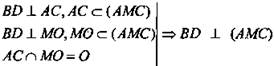 (по признаку перпендикулярности прямой и плоскости).
(по признаку перпендикулярности прямой и плоскости).
III. Решение задач
Решение письменно на доске и в тетрадях задачи № 130 (подробное решение в учебнике), № 134 (с помощью учителя), к доске вызвать сильного ученика.
№ 130
(Прежде чем приступать к решению задачи, повторить понятия: расстояние между двумя точками и расстояние от точки до прямой. Сформулировать определения этих понятий.)
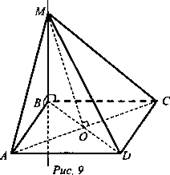
Дано: ABCD - квадрат; MB - прямая ![]()
![]() (рис. 9).
(рис. 9).
Найти: а) МА, MD, МС; б) ρ (М; АС), ρ (М; BD).
Решение:
1) АВ = ВС = CD = AD = n (по свойству сторон квадрата).
2) ΔАВМ и ΔСВМ - прямоугольные, так как ∠MBA = ∠МВС = 90°.
По теореме Пифагора: ![]() Получим,
Получим, ![]()
3) Так как BD - диагональ квадрата, то ![]()
4) Так как ∠MBA = ∠MBC = 90°, т.
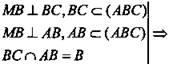 MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости). Значит, MB ⊥ BD, BD ⊂ (ABC) (по определению прямой, перпендикулярной плоскости).
MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости). Значит, MB ⊥ BD, BD ⊂ (ABC) (по определению прямой, перпендикулярной плоскости).
5) ΔMBD - прямоугольный (т. к. MB ⊥ BD, то ∠MBD = 90°). По теореме Пифагора: ![]()
6) ρ (M; BD) = MB (по определению расстояния от точки до прямой). Значит, ρ (М; BD) = m.
7) АО = ОС, ВО = OD (по свойству диагоналей квадрата). Так как ![]() то ΔAMC - равнобедренный (по определению) и МО - медиана (по определению), значит, МО - высота (по свойству медианы равнобедренного треугольника, проведенной к его основанию). Следовательно, МО ⊥ АС.
то ΔAMC - равнобедренный (по определению) и МО - медиана (по определению), значит, МО - высота (по свойству медианы равнобедренного треугольника, проведенной к его основанию). Следовательно, МО ⊥ АС.
8) ΔМВО - прямоугольный (так как MB ⊥ BD, то ∠MBO = 90°). ![]() По теореме Пифагора: МO2 = ВO2 + ВM2.
По теореме Пифагора: МO2 = ВO2 + ВM2. ![]()
9) МО = ρ (М; АС) (по определению расстояния от точки до прямой). ![]() (Ответ:
(Ответ: ![]() )
)
№ 134
(Учитель должен сформулировать идею решения задачи, если это необходимо.)
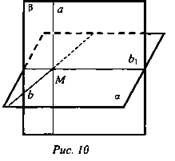
Дано: ![]()
![]() (рис. 10).
(рис. 10).
Доказать: b ⊂ α. (В ходе решения задачи учащимися следует задавать наводящие и уточняющие вопросы.)
Доказательство:
Предположим, что b ⊄ α (Что определяют две пересекающиеся прямые?)
По теореме о плоскости, проходящей через две пересекающиеся прямые, существует плоскость β, проходящая через прямые а и b. (Каково взаимное расположение плоскостей α и β?) ![]() Так как
Так как ![]() (по определению прямой перпендикулярной плоскости). Получим,
(по определению прямой перпендикулярной плоскости). Получим, ![]() противоречие. Значит, b ⊂ α.
противоречие. Значит, b ⊂ α.
IV. Подведение итогов
Домашнее задание
1) Повторить материалы § 1, с. 34-38.
2) Решить задачи: № 129, 136.
Дополнительная задача
Дан ΔABC, АВ = АС = ВС, CD ⊥ (ABC), AM = MB, DM = 15, CD = 12. Найти площадь ΔADB.