Поурочные разработки по геометрии 10 класс
Решение задач на применение ТТП, на угол между прямой и плоскостью - ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цель урока: закрепить изученный теоретический материал на практике.
Ход урока
I. Проверка домашнего задания
Два ученика на доске решают № 147, 151. После проверки этих задач остальные ученики задают дополнительные вопросы по теории. Остальные, решают № 150 (а) (можно самостоятельно с последующей проверкой).
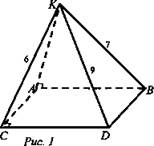
Дано: ABCD - прямоугольник; АК ⊥ (ABC), KD = 6 см, КВ = 7 см, КС = 9 см (рис. 1).
Найти: расстояние от точки К до (ABC).
Решение:
1. Длина АК - расстояние от К до (ABC) по определению.
2. Так как DC ⊥ AD, AD проекция KD, то по ТТП; DC ⊥ KD, значит, в ΔKDC ∠D = 90°. ![]()
3. СВ ⊥ КВ по ТТП; ![]()
![]()
4. Из ΔADC ∠D = 90°. ![]()
5. Из ΔКАС ∠A = 90°. ![]() (Ответ: 2 см.)
(Ответ: 2 см.)
Задача № 2
Диагонали квадрата ABCD пересекаются в точке О. SO - перпендикуляр к плоскости квадрата, SO = 4√2 см. а) Докажите равенство углов, образуемых прямыми SA, SC и SD с плоскостью квадрата, б) Найдите эти углы, если периметр ABCD равен 32 см.
Дано: ABCD - квадрат; BD ∩ АС = О, SO - перпендикуляр к (ABC), SO = 4√2 см, PABCD = 32 см (рис. 2).
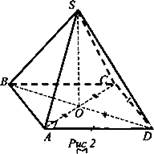
а) Доказать: ∠(SA, (ABC) = ∠(SB, (ABC)) = ∠(SC, (ABC)), ∠(SD, (ABC)).
б) Найти: ∠(SA, (ABC).
а) Доказательство:
1. SO ⊥ (ABC), AC, SD, SA, SB - наклонные; ОС, OD, OA, OB - их проекции; ∠(SC, (ABC)) = ∠SCO по определению; ∠(SD, (ABC) = ∠SDO и т.д.
2. ΔSOC = ΔSOD = ΔSOA = ΔSOB (как прямоугольные по двум катетам: SO - общая; ОС = OD = ОА = ОВ по свойству диагоналей квадрата).
3. ∠SCO = ∠SDO = ∠SAО = ∠SBO.
б) Решение:
 (Ответ: ∠(SA, (ABC) = 45°.)
(Ответ: ∠(SA, (ABC) = 45°.)
Вывод:
Если в тетраэдре DO - перпендикуляр и боковые ребра образуют равные углы с плоскостью основания, то точка О - центр окружности, описанной около основания.
Задача 3
В тетраэдре ABCD DO - перпендикуляр к (ABC). Докажите, что если перпендикуляры, проведенные из точки D к сторонам ΔABC, образуют равные углы с (ABC), то точка О - центр окружности, вписанной в ΔАВС.
Дано: ABCD - тетраэдр; ![]()
![]()
Доказать: О - центр окружности, вписанной в ΔABC.
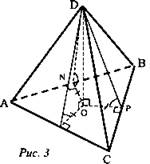
Доказательство:
1. ΔDON = ΔDOP = ΔDOM (как прямоугольные по общему катету и противолежащему острому углу).
2. ОМ = ОР = ON.
3. О - центр окружности, вписанной в ΔABC, так как она равноудалена от стороны ΔABC.
Вывод:
Если боковые грани тетраэдра наклонены к плоскости основания под одним углом, то основание высоты - это центр вписанной в основание окружности.
Домашнее задание
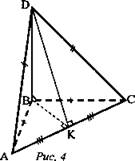
№ 154. Дано: ΔАВС, BD ⊥ (ABC), BD = 9 см, АС = 10 см, ВС = ВА = 13 см (рис. 4).
Найти: а) расстояние от точки D до АС; б) SΔACD.
Решение:
а) 1. DB - перпендикуляр, АС и DA - наклонные, так как ВА = ВС - проекции, то DA = DC.
2. ΔDАС - равнобедренный, DK - высота, медиана и биссектриса, DK - расстояние от точки D до АС.
![]()
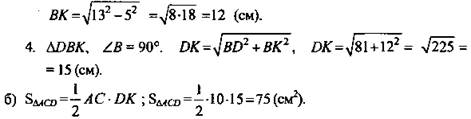
(Ответ: 15 см, 75 см2.)