Понятие многогранника - ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА - МНОГОГРАННИКИ

Цель урока:

- ввести понятие многогранника, призмы и их элементов.

Ход урока

I. Итоги контрольной работы

II. Актуализация опорных знаний Фронтальный опрос

1) Сумма углов треугольника.

2) Свойства углов при основании равнобедренного треугольника.

3) Чему равны острые углы равнобедренного прямоугольного треугольника?

4) Свойство катета, лежащего против угла в 30°.

5) Что называется углом между прямой и плоскостью?

6) Что называется линейным углом двугранного угла?

7) Найдите АС и ВС.

Решение (рис. 1):

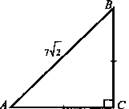
Вопрос учащимся: а) Какой треугольник? б) Какую теорему можно применить? АС = ВС = х,

8) Найдите AF, если A BCD - равнобедренная трапеция. ВС = 14 см, AD = 42 см (рис. 2).

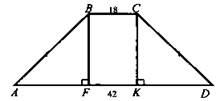
Решение:

Вопрос учащимся: а) Какое дополнительное построение нужно выполнить? (СК ⊥ AD); б) Рассмотреть треугольники AFB и CKD (доказать равенство); в) На основании того, что ΔAFB = ΔCKD, сделать вывод равенства AF = KD; г) AF = (AD - ВС) : 2 = (42 - 18) : 2 = 12 см.

III. Мотивация и сообщение темы урока

1) Напомнить известные учащимся понятия тетраэдра и параллелепипеда.

Заранее предложить двум учащимся выступить с небольшими сообщениями на темы: «Параллелепипед и его основные элементы» и «Тетраэдр и его основные элементы».

2) Слово учителя: Обратите внимание, что каждая из этих поверхностей ограничивает некоторое геометрическое тело, отделяет это тело от остальной части пространства. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.

Многие строения в окружающем нас мире, в частности, пирамида Хеопса, имеют форму многогранников. Поэтому для лучшей эксплуатации и моделирования зданий нужно изучить свойства многогранников.

Многие многогранники изобрел не человек, а создала природа в виде кристаллов, соли - куб, льда, хрусталя - «заточенная» с двух сторон призма.

(При объяснении и разговоре с учащимися использовать как можно больше разнообразных моделей, рисунков, чертежей).

Кристаллы граната, кварца, каменной соли.

IV. Объяснение темы

1) Вводятся элементы многогранников: грани, ребра, вершины, диагонали граней, диагонали многогранника (в соответствии с п. 25). Вопрос: из чего состоит поверхность многогранника? (Ответ: из многоугольников.)

Вывод: многоугольники - это грани.

Вопрос: что такое многоугольник? (Ответ: это плоская фигура, образованная замкнутым рядом прямоугольных отрезков.)

Вывод: прямолинейные отрезки - это ребра, а концы ребер - это вершины.

Отрезок, соединяющий две несоседние вершины одной грани, называется диагональю грани, а отрезок, соединяющий две вершины, не принадлежащие одной грани, - это диагональ многогранника.

2) В школе изучаются многогранники, Эйлерова характеристика которых равна 2, то есть В - Р + Г, где В - число вершин, Р - число ребер, Г - число граней.

Для закрепления понятий элементов многогранников следует с учащимися заполнить таблицу уже известных многогранников.

№	Наименование многогранника	В	Р	Г	Эйлерова характеристика
1	Тетраэдр	4	6	4	4 – 6 + 4 = 2
2	Параллелепипед	8	12	6	8 - 12 + 6 = 2
3	Куб	8	12	6	8 - 12 + 6 = 2

3) Вводится понятие призма, что это тоже многогранник, а также ее элементов: высота призмы, боковые грани, боковые ребра (в соответствие с п. 27).

Раздать на парту модели пирамиды или призмы и дать возможность самостоятельно подсчитать Эйлерову характеристику.

Затем сделать вывод на основании вычислений, как подсчитать число вершин, ребер и граней для любой пирамиды и любой призмы и продолжить заполнение таблицы.

4	n - угольная пирамида	n + 1	2n	n + 1	n + 1 – 2n + n + 1 = 2
5	n - угольная призма	2n	3n	n + 2	2n – 3n + n + 2 = 2

Равенство, которое выражает Эйлерову характеристику, было им доказано в 1752 году.

И оно верно для произвольного выпуклого многогранника. Наряду с ними существуют невыпуклые многогранники.

Дается определение в соответствие с п. 25 и рис. 67, 68, 69.

4) В любом многограннике сумма всех плоских углов при каждой его вершине меньше 360°.

Доказать это можно с помощью разверток, например, тетраэдр. Очевидно, что φ1 + φ2 + φ3 < 360°.

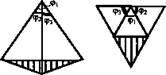
Параллелепипед (прямоугольный).

Вопрос: Сколько углов имеют общую вершину? (Ответ: три, причем все по 90°.)

Вывод: 90° + 90° + 90° = 270° < 360°.

V. Закрепление изученного материала

Контрольные вопросы

1) Объясните, что такое: а) многогранник; б) поверхность многогранника.

2) Какой многогранник называется выпуклым?

3) Дан куб - выпуклый многогранник (проверьте). Как, имея пилу, получить из деревянного куба модель невыпуклого многогранника?

4) Дан выпуклый многогранник. Что называют а) его гранью; б) его ребром; в) его вершиной?

5) Назовите известные вам многогранники.

а) Выпуклым или не выпуклым является каждый из них? б) Сколько граней, ребер и вершин у каждого?

6) Дан квадрат. На нем как на основании построены куб и пирамида. Сколько вершин, ребер и граней в полученном многограннике? Является ли он выпуклым?

В = 9; Г = 9; Р = 16; 9 - 16 + 9 = 2. Да.

7) Два тетраэдра имеют общую грань и расположены по разные стороны от нее. Сколько вершин, ребер и граней в полученном многограннике? Является ли он выпуклым?

В = 5; Г = 6; Р = 9; 5 - 9 + 6 = 2. Да.

8) Сколько трехгранных, двугранных и плоских углов: а) у тетраэдра; б) у параллелепипеда.

VI. Решение задач (применение знаний в стандартной ситуации)

№ 219. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ = 12 см, ВС = 5 см, угол между АС1 и (ABC) 45° (рис. 3).

Найти: ВВ1.

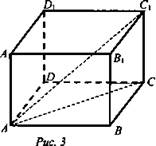
Решение: Проекцией АС1 на плоскость (ABC) является AC (СС1 ⊥ (ABC), значит, AC ⊥ СС1). Значит, ∠CAC1 = 45°. Имеем: ΔACC1 прямоугольный и равнобедренный АС = СС1 = ВВ1. Найдем АС: Значит, СС1 = ВВ1 = 13 см. (Ответ: 13 см.)

№ 220. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ = ВС, АС = 24 см, BD = 10 cm, AA1 = 10 см (рис. 4).

Найти: большую диагональ.

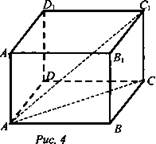
Решение: Большая диагональ АС1 (так как большая диагональ ромба АС является проекцией диагонали АС1, чем больше ее проекция, тем больше ее наклонная). ΔACC1 - прямоугольный треугольник. (Почему?)

(Ответ: 26 см.)

№ 223. Дано: ABCDA1B1C1D1 - куб, ABC1D1 - сечение. (рис. 5).

Найти: АВ; АС1.

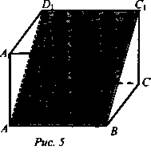
Решение:

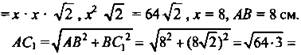
(Ответ: АВ = 8 см, АС1 = )

Домашнее задание

П. 25, 26, 27.

Вопросы: 1, 2, к гл. III. № 220 (решение на стр. 6); № 295 (а, б); № 295 (в, г) - по желанию, для более подготовленных учеников.

Дано: ABCDA1B1C1D1 - наклонный параллелепипед. ABCD - ромб. СС1 составляет одинаковые углы с DC и ВС, то есть ∠С1СВ = ∠C1D (рис. 6).

Доказать: а) СС1 ⊥ BD; б) BB1D1D — прямоугольник; в) BD ⊥ АА1С1 г) АА1С1 ⊥ BB1D1.

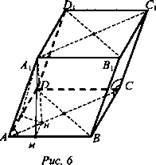
Доказательство: а) СС1 || АА1, ABCD - ромб.

Отсюда ∠A1AD = ∠A1AB. Построим А1Н ⊥ плоскости ABC, НМ ⊥ АВ, HN ⊥ AD, отрезки А1М и A1N. Нам надо доказать, что высота параллелепипеда А1Н проецируется в точку Н на диагонали АС. Так как по построению А1Н ⊥ АВ и MN ⊥ АВ, то по теореме о трех перпендикулярах имеем: A1М ⊥ АВ. Так как А1Н ⊥ AD и NH ⊥ AD, то по теореме о 3-х перпендикулярах имеем: A1N ⊥ AD. ΔА1АМ = ΔA1AN, (А1А - общая, они прямоугольные и имеют по равному острому углу). Отсюда следует, что AM = AN. ΔАНМ = ΔAHN, (так как они прямоугольные, гипотенуза АН - общая, AN = AM). Отсюда следует, что ∠НАМ = ∠HAN, то есть точка Н лежит на биссектрисе угла ромба, которая является диагональю ромба; а диагонали ромба взаимно перпендикулярны. Так как A1H ⊥ AC и А1А ⊥ DB (по теореме о 3-х перпендикулярах), но так как А1А || C1C, то C1C || DB.

Утверждение а) доказано.

б) Докажем, что BB1D1D - прямоугольник.

Так как D1D || DB и DD1 || В1В, то DD1B1B - параллелограмм.

В1В || A1D1, но так как доказано, что А1А ⊥ DB.

Значит, в параллелограмме D1DB1B ∠B1BD = 90°, и поэтому данный параллелограмм - прямоугольник.

в) Докажем, что BD ⊥ плоскости АА1С1.

DB ⊥ АС и DB ⊥ АА1 - по свойству диагоналей ромба. Отсюда DB ⊥ плоскости А1АСС1, то есть в) доказано.