Поурочные разработки по геометрии 10 класс
Параллельность прямой и плоскости - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) рассмотреть возможные случаи взаимного расположения прямой и плоскости в пространстве.
2) ввести понятие параллельности прямой и плоскости.
3) доказать признак параллельности прямой и плоскости.
Ход урока
I. Организационный момент
Проверить у доски решение задачи № 16.
Сообщить тему урока, сформулировать его цели.
II. Объяснение нового материала начать с рассмотрения взаимного расположения прямой и плоскости в пространстве
В каком случае прямая и плоскость параллельны (рис. 1. а, б, в)? Прямая и плоскость называются параллельными, если они не имеют общих точек.
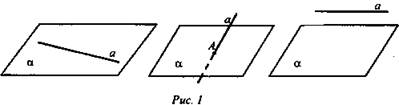
Показать на предметах обстановки классной комнаты прямые, параллельные плоскости пола.
На модели куба (рис. 2) укажите плоскости, параллельные прямой DC, прямой DD1.
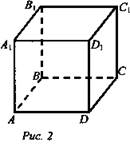
Как установить параллельность прямой и плоскости?
Обратите внимание на модель куба. DC || (AA1B1). В плоскости (AA1B1) имеется прямая АВ || DC; DC || (A1B1C1). В плоскости (А1В1С1) имеется прямая D1C1 || DC. Сделайте предположение. Наличие в плоскости α прямой b || а является признаком, по которому можно сделать вывод о параллельности прямой а и плоскости α.
Теорема:
Дано: а, α; а ∉ α; b ∈ α; а || b (рис. 3).
Доказать, что а || α.
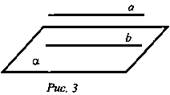
Доказательство: По условию b ∈ α; b || а.
Предположим, что а ∩ α, тогда по лемме о пересечении плоскости параллельными прямыми прямая b ∩ α, но это невозможно, так как b ∈ α. Следовательно, а ∩ α, поэтому а || α и теорема доказана.
Докажем два утверждения, которыми будем пользоваться при решении задач.
1. Если плоскость проходит через данную прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Дано: ![]() (рис. 4).
(рис. 4).
Доказать: а || b.
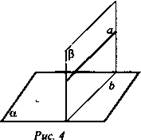
Доказательство: По условию ![]() значит, а || b, так как
значит, а || b, так как ![]()
2. Если одна из 2-х параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Дано: а || b; а; а || α (рис. 5).
Доказать: 1) b || α. 2) b ∈ α.
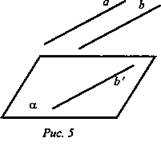
Доказательство: По условию а || b и α || а, следовательно, по лемме о пересечении плоскости параллельными прямыми ![]() то есть b || α или b ∈ α.
то есть b || α или b ∈ α.
III. Закрепление изученного материал.
Задача № 186
Дано: ![]()
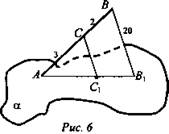
![]() АС : СВ = 3 : 2; ВВ1 = 20 см (рис. 6).
АС : СВ = 3 : 2; ВВ1 = 20 см (рис. 6).
Найти: СС1.
Решение:
1. Докажем, что точки А, С1, В1 лежат на одной прямой. Точка А и ВВ1 определяют плоскость β. β ∈ α = АВ1. Докажем, что С1 ∈ АВ1. Пусть С1 ∉ β, тогда ![]() что противоречит BB1 ∈ β. СС1 ∩ β. Следовательно, С1 ∈ АВ1.
что противоречит BB1 ∈ β. СС1 ∩ β. Следовательно, С1 ∈ АВ1.
2. Так как ![]() тогда
тогда ![]()
![]() (Ответ: 12 см..
(Ответ: 12 см..
Задача № 20
Дано: α, ABCD - трапеция, MN - средняя линия; MN ∈ α (рис. 7).
Доказать: Пересекает ли ВС и AD плоскость α.
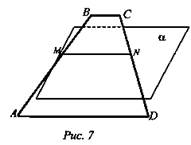
Доказательство: 1. Пусть ВС ∩ α, тогда ![]() получили противоречие, так как
получили противоречие, так как ![]()
Аналогично доказывается, что ![]()
IV. Подведение итогов
Домашнее задание П. 6, № 18 (a), 19, 21.
Задача № 18 а
Дано: А ∈ α; CС1 || ВВ1; АС = СВ, ВВ1 = 7 см.
Найти: СС1.
Решение:
Доказательство того, что С1 ∈ АВ1 дано в 18 (б). Так как С - середина АВ, то СС1 - средняя линия ΔABB1 ⇒ СС1 = 3,5. (Ответ: 3,5 см.)
Задача № 19
Дано: ABCD - параллелограмм; АВ ∩ α = К; ВС ∩ α = М (рис. 8).
Доказать, что AD ∩ α; DC ∩ α.
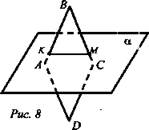
Доказательство: ![]() по лемме DC ∩ α. Аналогично AD ∩ α.
по лемме DC ∩ α. Аналогично AD ∩ α.
Задача № 21
Дано: ΔАВС и ΔABD не лежат в одной плоскости; MN || CD (рис. 9).
Доказать: MN ∩ (ABC); MN ∩ (ABD).
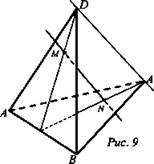
Доказательство:
![]()
![]() Следовательно, по лемме MN ∩ ABD и MN ∩ ABC. Что и требовалось доказать.
Следовательно, по лемме MN ∩ ABD и MN ∩ ABC. Что и требовалось доказать.