itle

Цели: повторить и закрепить изученный материал в ходе решения задач; учить учащихся умению применять изученные теоремы при решении задач; развивать логическое мышление.

Ход урока

I. Актуализация опорных знаний.

1. Провести фронтальный опрос учащихся по вопросам 1-15 на с. 49—50 без доказательств.

2. Устное решение задач:

1) В двух треугольниках равны по две стороны и по одному углу. Всегда ли равны эти треугольники?

2) В двух треугольниках равны по одной стороне и по два угла. Всегда ли равны эти треугольники?

3) Оба треугольника равносторонние и имеют только по одной равной стороне. Равны ли эти треугольники?

4) ΔСДЕ = ΔKFM и оба они равносторонние. Найдите периметр треугольника KFM, если сторона СД = 10 см.

II. Решение задач.

1. Решить задачу № 139 (по рис. 76) на доске и в тетрадях.

Решение (краткая запись):

1) ΔАВС = ΔСДА по трем сторонам, следовательно, ∠АВС = ∠СДА. Так как BE и DF - биссектрисы углов ABC и СДА, то 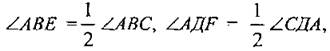откуда следует, что ∠АВЕ =∠ADF.

2) Из равенства треугольников ABC и СДА следует, что ∠ВАЕ = ∠ДСF. Далее, ∠АВЕ = ∠АДF = ∠СДF. Итак, ∠АВЕ = ∠СДF, ∠ВАЕ = ∠ДСF и АВ = СД по условию, значит, ΔАВЕ = ΔСДF по стороне и двум прилежащим к ней углам.

2. Решить задачу № 169 (по рис. 95) на доске и в тетрадях. Рассказать учащимся о способе измерения ширины озера (отрезка АВ) по заранее изготовленной таблице: «Чтобы измерить на местности расстояние между двумя точками А и В, из которых одна (точка А) недоступна, провешивают направление отрезка АВ и на его продолжении отмеряют на земле произвольный отрезок ВС. Выбирают на местности точку О, из которой видна точка А и можно пройти к точкам В и С. Провешивают прямые ВОЕ и СОД, отмеряют на местности ДО = ОС и ОЕ = ОВ. Затем идут по прямой ДЕ, глядя на точку А, пока не найдут точку F, которая лежит на прямой АО.

Тогда FE равно искомому расстоянию. Расстояние FE измеряют на земле с помощью рулетки».

3. Решить задачу № 176* на доске и в тетрадях.

Дано: ΔАВС = ΔA1B1C1;

АВ = А1В1; АС = А1С1; AM = А1М1.

AM и A1M1 - медианы треугольников.

Доказать: ΔАВС = ΔA1B1C1.

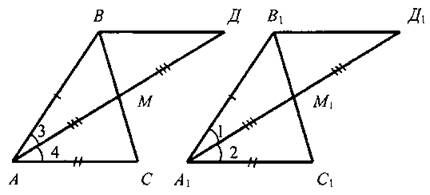
Доказательство:

Проведем отрезки МД = AM; М1Д1 = А1М1 и отрезки ВД; ВД1.

1) ΔВМД = ΔСМА по двум сторонам и углу между ними, поэтому ВД = АС; ∠Д = ∠4. Аналогично ΔВ1М1Д1 = ΔС1М1А1, откуда В1Д1 = А1С1; ∠Д1 = ∠2. Отсюда следует, что ВД = В1Д1.

2) ΔАВД = ΔА1В1Д1 по трем сторонам, поэтому ∠3 = ∠1, ∠Д = ∠Д1, значит, ∠4 = ∠2.

3) ∠A = ∠А1, так как ∠A = ∠4 + ∠3 = ∠2 + ∠1 = ∠A1. Таким образом, ΔАВС = ΔА1В1С1 по двум сторонам и углу между ними.

III. Самостоятельная работа проверочного характера.

Вариант I

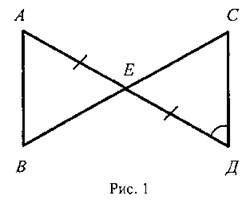
1. Докажите равенство треугольников АВЕ и ДСЕ на рисунке 1, если АЕ = ЕД, ∠А = ∠Д. Найдите стороны треугольника АВЕ, если ДЕ = 3 см, ДС = 4 см, ЕС = 5 см.

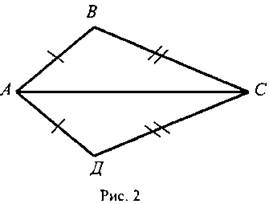
2. На рисунке 2 АВ = АД, ВС = СД. Докажите, что луч АС - биссектриса угла ВАД.

Вариант II

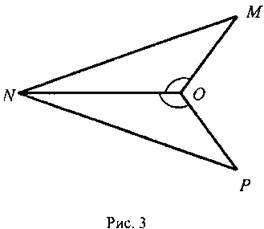
1. Докажите равенство треугольников MON и PON на рисунке 3, если ∠MON = ∠PON, а луч NO - биссектриса ∠MNP. Найдите углы треугольника NOP, если ∠MNO = 28°, ∠NMO = 42°, ∠NOM = 110°.

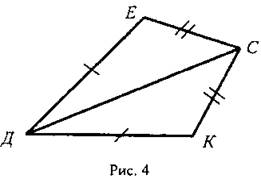
2. На рисунке 4 ДЕ = ДК, СЕ = СК. Докажите, что луч СД - биссектриса угла ЕСК.

Дополнительно (для тех учащихся, кто более подготовлен):

В треугольниках ABC и А1В1С1 АВ = А1В1, ∠А = ∠А1, ∠В = ∠В1. На сторонах ВС и В1С1 отмечены точки Д и Д1 так, что ∠САД = ∠С1А1Д1. Докажите, что: а) ΔАДС = ΔА1Д1С1; б) ΔАДВ = ΔА1Д1В1.

IV. Итоги урока.

Домашнее задание: повторить пункты 16-20 из § 2 и 3; решить задачи № 140; 172.