ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ

Цели: ввести определение параллелограмма, рассмотреть его свойства.

Ход урока

I. Проверка домашнего задания.

Обсудить решения домашних задач, ответить на вопросы учащихся.

II. Самостоятельная работа.

Вариант I

1. Найдите сумму углов выпуклого тринадцатиугольника.

2. Каждый угол выпуклого многоугольника равен 135°. Найдите число сторон этого многоугольника.

Вариант II

1. Найдите сумму углов выпуклого двенадцатиугольника.

2. Сумма углов выпуклого многоугольника с равными друг другу углами равна 1260°. Найдите число сторон этого многоугольника.

Вариант III
(для более подготовленных учащихся)

Каждый угол данного выпуклого многоугольника равен 150°. Найдите сумму углов выпуклого многоугольника, число сторон которого в два раза меньше, чем число сторон данного многоугольника.

III. Изучение нового материала.

1. Дать определение параллелограмма. Воспроизвести рисунок 157 из учебного пособия на доске (учащиеся – в тетрадях) и записать: «Параллелограмм АВСD». Предложить учащимся записать пары параллельных сторон: АВ || CD, BC || AD.

Обратить внимание учащихся на то, что определение параллелограмма позволяет сделать два вывода:

1) Если известно, что некоторый четырехугольник является параллелограммом, то можно сделать вывод о том, что его противоположные стороны параллельны.

2) Если известно, что у некоторого четырехугольника противоположные стороны попарно параллельны, то он является параллелограммом.

2. На закрепление определения параллелограмма можно предложить учащимся устные задания:

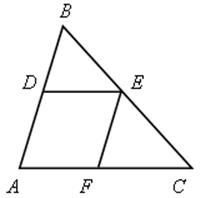
1) Дан АВС. Параллельно сторонам АВ и АС проведены прямые ЕF и DЕ. Определите вид четырехугольника АDЕF.

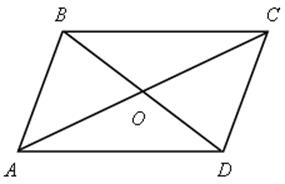
2) В параллелограмме АВСD проведена диагональ ВD. Докажите, чтоАВD = СDВ.

3) Прямая EF параллельна стороне АВ параллелограмма АВСD. Докажите, что АВЕF – параллелограмм.

3. Рассмотреть свойства параллелограмма.

4. Доказать, что в параллелограмме сумма углов, прилежащих к одной стороне, равна 180°.

IV. Закрепление изученного материала.

Решить задачи № 376 (а) – устно; № 376 (б), № 372 (а).

V. Итоги урока.

Если в условии задачи дано, что АВСD – параллелограмм, то можно использовать его свойства:

		АВ || CD, ВС || АD АВ = CD, ВС = АD А = C, В = D А + В = 180° и т. д. АО = ОC, ВО = ОD
АВСD – параллелограмм

Домашнее задание: вопросы 6–8, с. 114; №№ 372 (б), 376 (в, г), 374.

Для желающих можно выдать индивидуальное задание:

1. В параллелограмме АВСD на сторонах АD и ВС взяты точки К и Е соответственно так, что KВЕ = 90° и отрезок ЕK проходит через точку О пересечения диагоналей. Докажите, что ВО = ОЕ.

2. На сторонах АС и ВС треугольника АВС отмечены точки D и Е соответственно, а внутри треугольника – точка М так, что четырехугольник DСЕМ является параллелограммом и DЕ || АВ. Прямая DМ пересекает отрезок АВ в точке K, а прямая ЕМ – в точке Н. Докажите, что АK = НВ.

Указания к решению задач.

1. Последовательно доказываем, что ВОЕ = KОD, ВDЕ = ВKЕ, ЕD || ВK, ЕD = ВK, ВKЕ = ВЕD, ВKЕ = ВDЕ, KЕВ = DВЕ. Значит, ОВ = ОЕ.

2. В параллелограммах АDЕН и KDЕВ, АН = DЕ и KВ = DЕ. Значит, АН = KВ. Следовательно, АK = НВ.