ПРИМЕНЕНИЕ ПОДОБИЯ К ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ И РЕШЕНИЮ ЗАДАЧ - урок 3

Цель: рассмотреть задачу о пропорциональных отрезках в прямоугольном треугольнике.

Ход урока

I. Проверка домашнего задания.

1. Один ученик у доски записывает решение № 618:

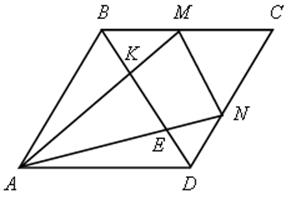
1) MN – средняя линия ВСD, МN || BD и MN = BD.

2) ВМК DАК (по двум углам).

.

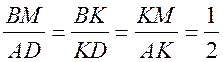3) ВD = ВK + KD, ВD = ВK + 2ВK, ВK = ВD.

4) АМN АKЕ (МN || BD).

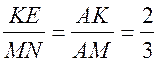, 2MN = 3KE.

5) ВD = 2 МN = 3KЕ, то есть KЕ = ВD.

6) ВK = KЕ = ЕD = ВD.

2. Остальные работают в это время устно:

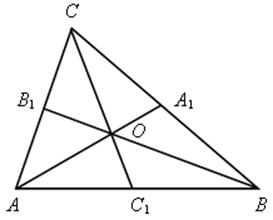
АА1, ВВ1, СС1 – медианы АВС.

Докажите, что

а) ;

б) ;

в) .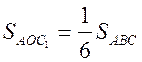

II. Объяснение нового материала.

1. Ввести понятие среднего геометрического (среднего пропорционального) двух отрезков.

2. Решить устно задачи:

а) Найти длину среднего геометрического отрезков АВ и СD, если АВ = 8 см, СD = 50 см.

б) Найти длины отрезков KL и MN, если один из них в четыре раза больше другого, а длина их среднего пропорционального равна 12 см.

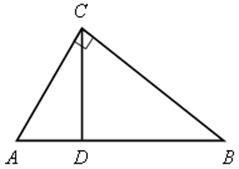
3. Устно: доказать, что

а) АВС АСD;

б) АВС СВD;

в) СВD АСD.

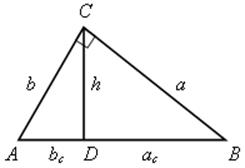
4. Из доказанного обосновать:

а) CD = .

б) AC = .

BC = .

5. Дать запись:

III. Закрепление изученного материала.

№ 572 (а, в).

а) Решение.

h = = 5 ∙ 4 = 20.

c = ac + bc = 25 + 16 = 41.

a = .

b = .

в) Решение.

b = ; b2 = c ∙ bc, 144 = c ∙ 6, c = 24.

c2 = a2 + b2; 576 = a2 + 144; a2 = 432; a = 12.

a = ; a2 = c ∙ ac; 432 = 24 ∙ ac; ac = 18.

№ 573 (устно).

ac = ; bc = .

№ 574 (а). I способ.

Решение

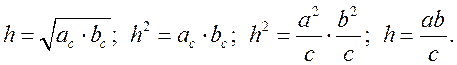
II способ.

Решение

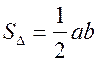или .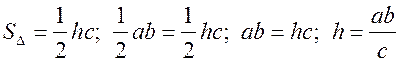

№ 575.

1) Пусть k – коэффициент пропорциональности, тогда а = 3k, b = 4k.

По теореме Пифагора с2 = а2 + b2;

502 = 9k2 + 16k2 ;

k2 = 100;

k = 10;

a = 30 (мм), b = 40 (мм).

2) ac = 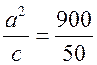= 18 (мм);

bc = 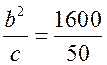= 32 (мм).

№ 578. (Решена в учебнике.) Законспектировать в тетрадях.

IV. Итоги урока.

Домашнее задание: вопросы 10, 11, с. 161; №№ 572 (б), 574 (б), 576.

№ 576.

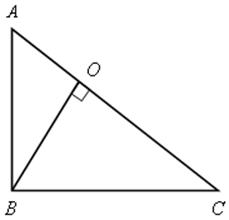
Решение

Пусть АВ = 6х, тогда ВС = 5х.

По теореме Пифагора AC = ==.

По доказанному в задаче № 573

AO = 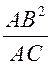, OC = 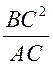, AO – OC = 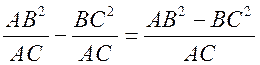= 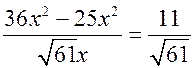x.

АО – ОС = 11, поэтому .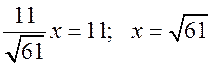

АС = 61 см.