Поурочные разработки по геометрии 9 класс
Скалярное произведение в координатах. Свойства скалярного произведения векторов - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
Цели: ввести понятие скалярного произведения в координатах; изучить свойства скалярного произведения векторов и закрепить их знание при решении задач.
Ход урока
I. Проверочная работа (10 мин).
Вариант I
1. Известно, что ![]() , где
, где ![]() и
и ![]() – координатные векторы. Выпишите координаты вектора
– координатные векторы. Выпишите координаты вектора ![]() .
.
2. Дан вектор ![]() (0; 5). Запишите разложение вектора
(0; 5). Запишите разложение вектора ![]() по координатным векторам
по координатным векторам ![]() и
и ![]() .
.
3. Даны векторы ![]() (–1; 2) и
(–1; 2) и ![]() (2; 1). Найдите координаты суммы векторов
(2; 1). Найдите координаты суммы векторов ![]() и
и ![]() .
.
4. Найдите координаты вектора ![]() , если
, если ![]() (–3; 0).
(–3; 0).
5. Даны векторы ![]() (5; 6) и
(5; 6) и ![]() (–2; 3). Найдите координаты вектора
(–2; 3). Найдите координаты вектора ![]() .
.
6. Две стороны треугольника равны 7 и 3 см, а угол между ними равен 120°. Найдите третью сторону треугольника.
7. в треугольнике АВС угол А = 45°, АВ = 2, АС = 3. Вычислите ![]() .
.
8. Скалярное произведение ненулевых векторов ![]() и
и ![]() равно нулю. Чему равен угол между векторами
равно нулю. Чему равен угол между векторами ![]() и
и ![]() ?
?
Вариант II
1. Дан вектор ![]() (3; 0). Запишите разложение вектора по координатным векторам
(3; 0). Запишите разложение вектора по координатным векторам ![]() и
и ![]() .
.
2. Известно, что ![]() , где
, где ![]() и
и ![]() – координатные векторы. Выпишите координаты вектора
– координатные векторы. Выпишите координаты вектора ![]() .
.
3. Найдите координаты вектора –![]() , если
, если ![]() (0; –2).
(0; –2).
4. Даны векторы ![]() (2; –1) и
(2; –1) и ![]() (3; –1). Найдите координаты разности векторов
(3; –1). Найдите координаты разности векторов ![]() и
и ![]() .
.
5. Даны векторы ![]() (–1; 9) и
(–1; 9) и ![]() (3; –2). Найдите координаты вектора
(3; –2). Найдите координаты вектора ![]() .
.
6. В треугольнике МРQ угол M = 135°; МР = 5, МQ = 2![]() . Вычислите
. Вычислите ![]() .
.
7. Две стороны треугольника равны 3 и 9 м, а угол между ними равен 60°. Найдите третью сторону треугольника.
8. Чему равно скалярное произведение координатных векторов ![]() и
и ![]() ?
?
II. Изучение нового материала.
1. Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов.
2. Изучение теоремы о скалярном произведении векторов в координатах и свойств скалярного произведения полезно построить так, чтобы учащиеся сами проводили алгебраические преобразования.
Полученные результаты можно записать в тетради и вынести в настенную таблицу:
Скалярное произведение в координатах
![]()
![]()
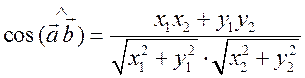
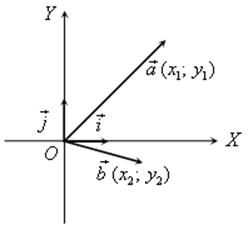
Свойства скалярного произведения векторов:
1) ![]() ≥ 0 (
≥ 0 (![]() > 0 при
> 0 при ![]()
![]() 0).
0).
2) ![]() ;
;
3) ![]() .
.
4) ![]() .
.
III. Закрепление изученного материала.
1. Решить задачу № 1043 (объясняет учитель):
Дано: ![]() = 8;
= 8; ![]() = 15;
= 15; ![]() АВС = 120°.
АВС = 120°.
Найти: ![]() .
.
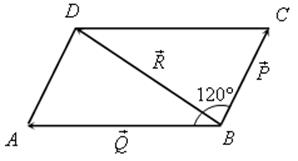
Решение
Пусть ![]() ;
; ![]()
![]() , тогда по правилу треугольника
, тогда по правилу треугольника ![]() (или по правилу параллелограмма вектор
(или по правилу параллелограмма вектор ![]() есть равнодействующая сила
есть равнодействующая сила ![]() ).
).
![]() C = 180° – 120° = 60° (сумма односторонних углов равна 180°). По теореме косинусов из треугольника ВСD найдем ВD.
C = 180° – 120° = 60° (сумма односторонних углов равна 180°). По теореме косинусов из треугольника ВСD найдем ВD.
BD2 = BC2 + CD2 – 2BC ∙ CD ∙ cos C = 82 + 152 – 2 ∙ 8 ∙ 15 ∙ ![]() = 64 + 225 – 120 = 169;
= 64 + 225 – 120 = 169;  = 169;
= 169; ![]() = 13.
= 13.
Ответ: 13.
2. Решить задачи № 1044 (а, б).
3. Устно № 1045.
4. Решить задачи № 1046, 1047 (б, в) на доске и в тетрадях.
5. Решить задачу № 1051.
Решение
 1 ∙ 2 cos 60° + 2 ∙ 2 cos 60° = 2 ∙
1 ∙ 2 cos 60° + 2 ∙ 2 cos 60° = 2 ∙ ![]() + 4 ∙
+ 4 ∙ ![]() = 1 + 2 = 3.
= 1 + 2 = 3.
Ответ: 3.
6. Решить задачу № 1049 на доске и в тетрадях (для угла А объясняет учитель):
Решение
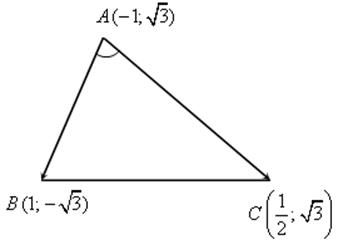
1) cos A = 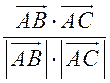
![]()
![]()
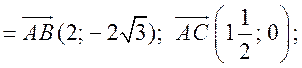
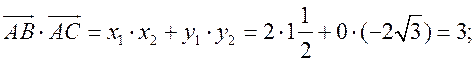

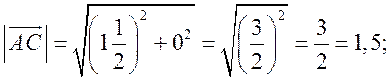
cos A = 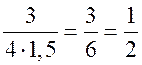 ; cos A =
; cos A = ![]() , то
, то ![]() A = 60°.
A = 60°.
2) cos B =  ;
; ![]()
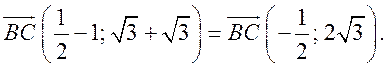
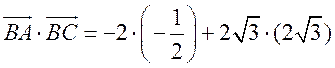 = 1 + 12 = 13;
= 1 + 12 = 13;

BC = 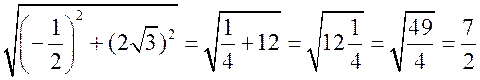 = 3,5;
= 3,5;
cos B = 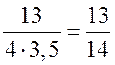 ≈ 0,9286;
≈ 0,9286; ![]() B находим по таблицам Брадиса:
B находим по таблицам Брадиса: ![]() B ≈ 21°47′.
B ≈ 21°47′.
3) ![]() C = 180° – 60° – 21°47′ ≈ 98°13′.
C = 180° – 60° – 21°47′ ≈ 98°13′.
Ответ: ![]() A = 60°;
A = 60°; ![]() B ≈ 21°47′;
B ≈ 21°47′; ![]() C ≈ 98°13′.
C ≈ 98°13′.
7. Решить задачу № 1052.
Решение
![]()
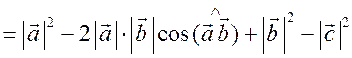 = 52 – 2 ∙ 5 ∙ 2 cos 90° + 22 – 42 = 25 + 4 – 16 = 13;
= 52 – 2 ∙ 5 ∙ 2 cos 90° + 22 – 42 = 25 + 4 – 16 = 13; ![]() = 13.
= 13.
Ответ: 13.
8. Решить задачу № 1066.
Решение
По условию 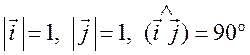 .
.
![]()
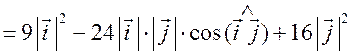 = 9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25.
= 9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25.
![]() = 25, тогда
= 25, тогда ![]() = 5.
= 5.
Ответ: 5.
IV. Итоги урока.
Домашнее задание: изучить материал пунктов 101–104; ответить на вопросы 17–20 на странице 271 учебника; решить №№ 1044 (в), 1047 (а), 1054 (разобрать решение задачи и записать в тетрадь).