Правильный многоугольник. Окружность, описанная около правильного многоугольника - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА

Цели: повторить ранее изученный материал о сумме углов выпуклого многоугольника, о свойстве биссектрисы угла, теорему об окружности, описанной около треугольника, признак равнобедренного треугольника; сформировать у учащихся понятия «правильный многоугольник», «многоугольник, вписанный в окружность»; выработать умение формулировать и доказывать теорему об окружности, описанной около правильного многоугольника.

Ход урока

I. Анализ контрольной работы.

 

II. Актуализация опорных знаний учащихся.

1. Повторить формулу суммы углов выпуклого многоугольника и записать ее.

2. Сформулировать свойство биссектрисы угла и признак равнобедренного треугольника.

3. Повторить теорему об окружности, описанной около треугольника.

4. Устно решить задачи:

1) Сколько сторон имеет n-угольник, если сумма его внутренних углов равна: а) 1260°; б) 1980°?

2) Назовите выпуклый четырехугольник, у которого все внешние углы прямые.

3) Сколько сторон имеет выпуклый многоугольник, если сумма его внутренних углов равна сумме внешних?

4) Сколько сторон имеет выпуклый многоугольник, если все его внешние углы тупые?

5. Решить задачи на доске и в тетрадях:

1) Все углы выпуклого пятиугольника равны друг другу. Найдите величину каждого угла.

2) Докажите, что треугольник, две высоты которого равны, является равнобедренным.

3) Четырехугольник АВСD вписан в окружность. Докажите, что А + С = В + D.

 

III. Изучение нового материала.

1. Ввести понятие правильного многоугольника.

2. Задать учащимся вопросы:

1) Какие правильные многоугольники уже рассматривались в курсе геометрии?

2) Приведите примеры такого выпуклого многоугольника, у которого:

а) все стороны равны, но он не является правильным (ромб с острым углом);

б) все углы равны, но он не является правильным (прямоугольник с неравными сторонами).

3. Предложить учащимся вывести формулу для вычисления угла правильного многоугольника: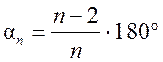

4. Решить задачи № 1081 (в) и 1083 (в) на доске и в тетрадях.

5. Формулировка и доказательство теоремы об окружности, описанной около правильного многоугольника (рис. 307).

IV. Закрепление изученного материала.

1. Решить задачи №№ 1086 и 1084 (б, д).

решени.

№ 1086.

Примечание. Воспользоваться тем, что биссектриса любого угла правильного многоугольника проходит через центр вписанной окружности.

№ 1084: б) Градусная мера дуги всей окружности равна 360°; количество сторон правильного многоугольника равно 360° : 30° = 12 (сторон); д) 360° : 18° = 20 (сторон).

Ответ: б) 12, д) 20.

2. Обсудить решения задач № 1080 и 1082 (устно).

 

V. Итоги урока.

Домашнее задание: изучить материалы пунктов 105–106; ответить на вопросы 1–3, с. 290; решить задачи №№ 1081 (а, д), 1083 (г), 1084 (а, в), 1129.