Поурочные разработки по геометрии 9 класс
Решение задач - урок 5 - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА
Цели: закрепить знания учащихся по изученной теме «Длина окружности и площадь круга»; научить учащихся применять изученные формулы при решении задач; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Повторить определения окружности, круга, кругового сектора и кругового сегмента.
2. Записать на доске и в тетрадях формулы для вычисления длины окружности, длины дуги окружности; для вычисления площади круга, площади кольца, площади кругового сектора.
II. Решение задач.
1. Решить задачу № 1112.
Решение
l = 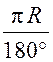 ∙ ; l = 24 см; = 38°. Найдем: R: R =
∙ ; l = 24 см; = 38°. Найдем: R: R = 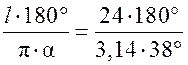 ≈ 36,3 (см).
≈ 36,3 (см).
ответ: ≈ 36,3 см.
2. Решить задачу № 1113 (самостоятельно).
3. Решить задачу № 1123 на доске и в тетрадях.
Решение
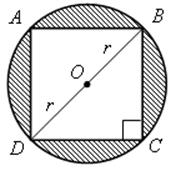
АВСD – квадрат; DО = ОВ = r; Sкруга = πr2; Sквадрата = а2,
ВD = 2r; из ДВСD по теореме Пифагора найдем сторону квадрата АВСD: а2 + а2 = (2r)2; 2а2 = 4r2; а2 = 2r2; тогда Sквадрата = 2r2.
Найдем площадь оставшейся части круга: S = Sкруга – Sквадрата = πr2 – 2r2 = r2 (π – 2).
Ответ: r2 (π – 2).
4. Решить задачу № 1116 (б).

Решени.
АСD – прямоугольный; ![]() А = , СD = а. АD = 2R (диаметр),
А = , СD = а. АD = 2R (диаметр), ![]() АСD = 90° (вписанный угол, опирающийся на диаметр, прямой). Найдем АD.
АСD = 90° (вписанный угол, опирающийся на диаметр, прямой). Найдем АD.
Sin =![]() ; AD =
; AD =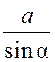 , тогда радиус R описанной около прямоугольного треугольника окружности равен R =
, тогда радиус R описанной около прямоугольного треугольника окружности равен R =![]() AD =
AD =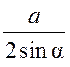 . Площадь круга равна S = πR2 =
. Площадь круга равна S = πR2 =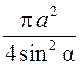 .
.
Ответ: 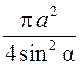 .
.
5. Решить задачи:
1) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 12 дм2. Найдите радиусы окружностей, если один их них в два раза больше другого.
Ответ: ![]() дм;
дм; ![]() дм.
дм.
2) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2. Найдите площади этих кругов, ограниченных этими окружностями, если радиус одной из них в три раза больше, чем радиус другой.
Ответ: 1 см2 и 9 см2.
6. Решить задачу № 1108 (самостоятельно).
III. Самостоятельная работа (10–15 мин).
Вариант I
Решить задачи №№ 1102 (в), 1115 (б), 1109 (в), 1104 (б).
Вариант II
Решить задачи №№ 1102 (г), 1115 (а), 1109 (г), 1116 (а).
IV. Итоги урока.
Домашнее задание: повторить материал пунктов 105–112; решить задачи №№ 1107, 1132, 1137.