Поурочные разработки по геометрии 9 класс
Многогранники. Объем тела - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
Цели: повторить понятие площади плоских фигур, ввести понятие объема тела, единиц измерения объемов тел; изучить основные свойства объемов и прямоугольного параллелепипеда; познакомить учащихся с принципом Кавальери; развивать логическое мышление учащихся.
Ход урока
I. Проверка домашнего задания.
1. Проверить по тетрадям решение учащимися задач № 1190 (б) и № 1234 (б).
2. По готовому на доске чертежу параллелепипеда построить сечение параллелепипеда плоскостью, проходящей через:
а) точки D, С и В1;
б) точки В, K и L, где K – середина ребра АА1, а L – середина СС1.
(Это задача № 1235 на с. 337 учебника.)
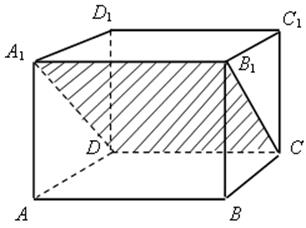
Решение
а) проводим отрезок СВ1, затем строим прямую DА1, параллельную В1С. Параллелограмм СDА1В1 – искомое сечение.
б) По условию АK = KА1 и СL = C1L. Проводим отрезки KВ и BL. Проводим отрезок D1L, параллельный отрезку KВ.
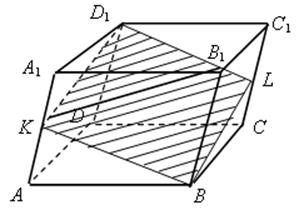
Соединяем отрезком точки K и D1, принадлежащие одной плоскости АDD1А1. параллелограмм KВLD1 – искомое сечение.
II. Изучение нового материала.
1. Повторить понятие площади плоской фигуры.
2. Понятие объема тела вводится по аналогии с понятием площади плоской фигуры. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называется кубическим сантиметром и обозначается так: 1 см3. Аналогично определяются кубический метр (м3), кубический миллиметр (мм3) и т. д.
3. Прочитать по учебнику текст (с. 314 и 315) и записать в тетрадях основные свойства объемов:
1) Равные тела имеют равные объемы.
2) Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел (рис. 347): V = V1 + V2.
4. Разобрать по рисунку учебника (рис. 348) принцип Кавальери.
5. Когда мы говорим о размерах комнаты, имеющей форму прямоугольного параллелепипеда, то обычно употребляем слова «длина», «ширина» и «высота», имея в виду длины трех ребер с общей вершиной. В геометрии эти три величины объединяются общим названием: измерения прямоугольного параллелепипеда (рис. 349, с. 317 учебника).
6. У прямоугольника два измерения – длина и ширина. При этом, как мы знаем, квадрат диагонали прямоугольника равен сумме квадратов двух его измерений (по теореме Пифагора для прямоугольника). Оказывается, что аналогичным свойством обладает и прямоугольный параллелепипед: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. (Используя рисунок 349, провести доказательство этого свойства. рисунок 349 заранее начертить на доске.)
Доказательство записывать на доске и в тетрадях:
АС12 = АС2 + СС12;
АС2 = АВ2 + АD2;
СС1 = ВВ1 = АА1,
следовательно, АС12 = АВ2 + АD2 + АА12.
7. Еще одно свойство прямоугольного параллелепипеда. Мы знаем, что площадь прямоугольника равна произведению его измерений. Аналогично объем прямоугольного параллелепипеда равен произведению трех его измерений.
![]()
Для доказательства этого утверждения воспользуемся принципом Кавальери (прочитать доказательство по учебнику на с. 317–319, используя рисунок 350).
8. В прямоугольном параллелепипеде с измерениями a, b, c, изображенном на рисунке учебника (рис. 350, б), площадь S основания равна ас, а высота h равна боковому ребру: h = b.
Поэтому формулу V = a ∙ b ∙ c можно записать в виде ![]() , то есть объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
, то есть объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
III. Выполнение упражнений и решение задач.
1. Решить задачу № 1193 (б; в).
Задачу № 1193 (в) решить на доске и в тетрадях.
Решение
a = ![]() ; b = 7; с = 9. Найти диагональ d.
; b = 7; с = 9. Найти диагональ d.
d2 = a2 + b2 + c2 (свойство диагонали прямоугольного параллелепипеда).
d2 = (![]() )2 + 72 + 92 = 39 + 49 + 81 = 169; d =
)2 + 72 + 92 = 39 + 49 + 81 = 169; d =![]() = 13.
= 13.
Ответ: 13.
Задачу № 1193 (б) учащиеся решают самостоятельно.
Решение
а = 8; b = 9; с = 12. Найти d.
d2 = a2 + b2 + c2 = 82 + 92 + 122 = 64 + 81 + 144 = 289; d1 =![]() = 17;
= 17;
d2 = –![]() = –17 не удовлетворяет условию задачи.
= –17 не удовлетворяет условию задачи.
Ответ: 17.
2. Решить задачу № 1194 на доске и в тетрадях.
Решение
Ребро куба равно а. Найти диагональ этого куба.
d2 = a2 + a2 + a2 = 3a2; d = ![]() = a
= a![]() .
.
Ответ: a![]() .
.
3. Решить задачу № 1195.
Решение
1) V = V1 + V2.
2) V1 – ![]() V1 =
V1 = ![]() V1; тогда V =
V1; тогда V = ![]() V1 + V2.
V1 + V2.
4. Объем куба равен кубу его стороны, то есть ![]() .
.
Найдите объем куба со стороной, равной 3 см; 2![]() дм.
дм.
5. Разобрать по учебнику решение задачи № 1198 (с. 323, используя рис. 357).
Записать в тетрадях: «Объем призмы равен произведению площади основания на высоту».
![]() .
.
6. Решить задачу № 1197.
Учитель объясняет решение задачи.
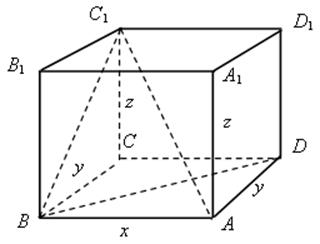
Решение
АС1 = 13 см; ВD = 12 см; ВС1 = 11 см.
Обозначим измерения прямоугольного параллелепипеда x, y, z.
Применим теорему Пифагора:
1) Для Δ АВD имеем х2 + y2 = 122. (1)
2) Для Δ ВСС1 имеем y2 + z2 = 112. (2)
3) По свойству диагонали прямоугольного параллелепипеда имеем х2 + у2 + z2 = 132. (3)
4) Подставим в равенство (3) равенство (1), получим 122 + z2 = 132, отсюда z2 = 132 – 122, тогда z =![]() = 5; z = 5.
= 5; z = 5.
5) Подставим в равенство (2) значение z = 5, найдем y2 + 52 = 112; у2 = 121 – 25 = 96; у =![]() ; у =
; у =![]() .
.
6) Подставим значение y2 = 96 в равенство (1), получим х2 + 96 = 144; х2 = 144 – 96 = 48; ![]() ;
; ![]() .
.
7) Найдем объем V = x ∙ y ∙ z = 4![]() ∙ 4
∙ 4![]() ∙ 5 = 80
∙ 5 = 80![]() = 80
= 80![]() = 80
= 80![]() = 240
= 240![]() (см3).
(см3).
Ответ: 240![]() см3.
см3.
IV. Итоги урока.
1. Объясните, как измеряются объемы тел.
2. Сформулируйте основные свойства объемов.
3. Объясните, в чем заключается принцип Кавальери.
4. Что такое измерения прямоугольного параллелепипеда?
5. Сформулируйте свойство диагонали прямоугольного параллелепипеда.
6. Чему равен объем прямоугольного параллелепипеда?
Домашнее задание: изучить материал пунктов 122–123; сделать чертеж (рис. 357) и записать в тетрадях решение задач №№ 1193 (а), 1196, 1198.