Решение задач. Произведение вектора на число - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ

Цели: закрепить изученный материал в ходе решения задач; развивать логическое мышление учащихся.

Ход урока

I. Устная работа.

По заранее заготовленным чертежам на доске устно решить задачи:

1. На рисунке 1 ABCD – параллелограмм, O – точка пересечения диагоналей. Выразите через векторы и векторы: а) б) где М – точка на стороне BC, такая, что МВ : MC = 3 : 2; в) где K – точка на стороне AD, такая, что АK : KD = 1 : 3; г) где N – точка на диагонали AC, такая, что ON = NC.

Рис. 1

2. На рисунке 2 ABCD – трапеция, О – точка пересечения диагоналей, ВС || AD, AD = 2BC. Выразите через векторы и векторы: а) б)

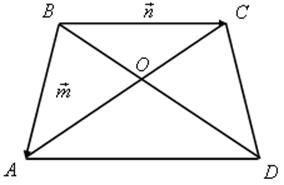
Рис. 2

II. Решение задач.

1. решить задачу № 782 на доске и в тетрадях.

Решение

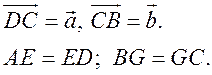
Из треугольника ECD (рис. 3) найдем по правилу вычитания векторов: тогда

Из треугольника ABG по правилу сложения векторов имеем отсюда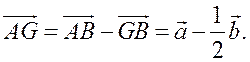

2. решить задачу № 802 на доске и в тетрадях.

III. Проверочная самостоятельная работа.

Вариант I

1. Начертите два неколлинеарных вектора и так, что = 3 см, = 2 см. Постройте

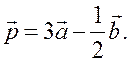
2. Четырехугольник KMNP – параллелограмм. Выразите через векторы и векторы и , где А – точка на стороне PN, такая, что PA : AN = 2 : 1, B – середина отрезка MN.

Вариант II

1. Начертите два неколлинеарных вектора и так, что = 2 см, = 3 см. Постройте вектор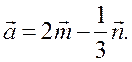

2. В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 1 : 2. Выразите векторы и через векторы и .

Вариант III (для более подготовленных учащихся)

1. В треугольнике ABC угол C = 90°, AC = 3 см, BC = 4 см. Постройте вектор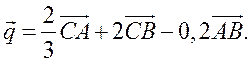

2. В трапеции ABCD AB || CD, AB = 3CD. Выразите через векторы и векторы и , где M – середина стороны BC, а N – точка на стороне AB, такая, что AN : NВ = 2 : 3.

IV. Итоги урока.

Домашнее задание: повторить материал пунктов 76–83; ответить на вопросы 1–17, с. 213–214 учебника; решить задачи №№ 783 и 804.