Средняя линия трапеции - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ

Цели: ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов; упражнять учащихся в решении задач.

Ход урока

I. Проверка усвоения учащимися материала.

1. Устно ответить на вопросы:

1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы и и противоположно направленные векторы и .

2) Какой вектор называется произведением данного вектора на данное число?

3) Могут ли векторы и быть неколлинеарными?

4) Сформулируйте основные свойства умножения вектора на число.

2. Решить задачу на доске и в тетрадях по готовому чертежу:

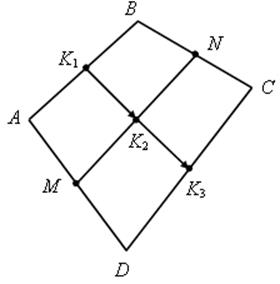
Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC = 3 : 4.

Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.

Решение

Пусть K1 – середина AB, K2 – середина MN, K3 – середина CD. Согласно задаче 2 из п. 84 имеем 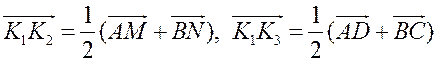. Из условия следует, что 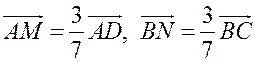, поэтому .

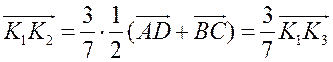Таким образом, векторы и коллинеарные, и, значит, точки K1, K2 и K3 лежат на одной прямой.

II. Объяснение нового материала.

1. Определение трапеции. Виды трапеций.

2. Определение средней линии трапеции.

3. Доказательство теоремы о средней линии трапеции (проводит сам учитель).

При доказательстве теоремы целесообразно использовать результат задачи 2, решенной на предыдущем уроке.

Доказательство можно оформить на доске и в тетрадях в виде следующей краткой записи:

Дано: ABCD – трапеция, AD || BC, M – середина стороны AB; N – середина стороны CD (рис. 266 учебника).

Доказать: MN || AD, MN = .

Доказательство

1) Согласно рассмотренной в классе задаче 1 .

2) Так как , то и, значит, MN || AD.

3) Так как , то = AD + BC, поэтому MN = (AD + BC).

III. Закрепление изученного материала (решение задач).

1. Решить на доске и в тетрадях задачу № 793.

Решение

Пусть a и b – основания трапеции, тогда а + b = 48 – (13 + 15) = 20 (см); средняя линия MN = 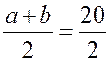= 10 (см).

Ответ: 10 см.

2. Решить задачу № 795.

3. Решить задачу № 799 на доске и в тетрадях.

Решение

Пусть BK – перпендикуляр, проведенный к основанию AD данной трапеции.

Тогда KD = AD – AK.

Но AK = 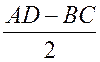, поэтому KD = AD –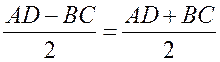, то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.

Ответ: 7 см.

IV. Проверочная самостоятельная работа.

Вариант I

Точка K делит отрезок MN в отношении MK : KN = 3 : 2. Выразите вектор через векторы и , где A – произвольная точка.

Вариант II

Точка A делит отрезок EF в отношении EA : AF = 2 : 5. Выразите вектор через векторы и , где K – произвольная точка.

V. Итоги урока.

Домашнее задание: изучить материал пункта 85; ответить на вопросы 18–20, с. 214 учебника; решить задачи №№ 787, 794, 796.

Основные требования к учащимся:

В результате изучения параграфа учащиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 782–787; 793–799.